Wprowadzenie do rozkładu wykładniczego

Rozkład wykładniczy to rozkład prawdopodobieństwa używany do modelowania czasu, jaki musimy poczekać, aż nastąpi określone zdarzenie.

Rozkład ten można wykorzystać do odpowiedzi na pytania takie jak:

• Jak długo sprzedawca powinien czekać, aż klient wejdzie do jego sklepu?
• Jak długo laptop będzie działał, zanim się zepsuje?
• Jak długo akumulator samochodowy będzie działał, zanim padnie?
• Jak długo powinniśmy czekać do kolejnej erupcji wulkanu w danym regionie?

W każdym scenariuszu chcemy obliczyć, jak długo będziemy musieli czekać, aż nastąpi określone zdarzenie. Zatem każdy scenariusz można modelować przy użyciu rozkładu wykładniczego.

Rozkład wykładniczy: PDF i CDF

Jeśli zmienna losowa X ma rozkład wykładniczy, wówczas można zapisać funkcję gęstości prawdopodobieństwa X :

fa (x; λ) = λe ^-λx

Złoto:

• λ: parametr szybkości (obliczany jako λ = 1/μ)
• e: Stała w przybliżeniu równa 2,718

Funkcja dystrybucji skumulowanej

F (x; λ) = 1 – e ^-λx

W praktyce CDF jest najczęściej używany do obliczania prawdopodobieństw związanych z rozkładem wykładniczym.

Załóżmy na przykład, że średnia liczba minut pomiędzy erupcjami pewnego gejzeru wynosi 40 minut. Jakie jest prawdopodobieństwo, że na erupcję będziemy musieli poczekać mniej niż 50 minut?

Aby rozwiązać ten problem, musimy najpierw obliczyć parametr szybkości:

• λ = 1/µ
• λ = 1/40
• λ = 0,025

Możemy podstawić λ = 0,025 i x = 50 do wzoru CDF:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 50) = 1 – e ^-0,025(50)
• P(X ≤ 50) = 0,7135

Prawdopodobieństwo, że na kolejną erupcję będziemy musieli poczekać mniej niż 50 minut, wynosi 0,7135 .

Wizualizuj rozkład wykładniczy

Poniższy wykres przedstawia funkcję gęstości prawdopodobieństwa zmiennej losowej

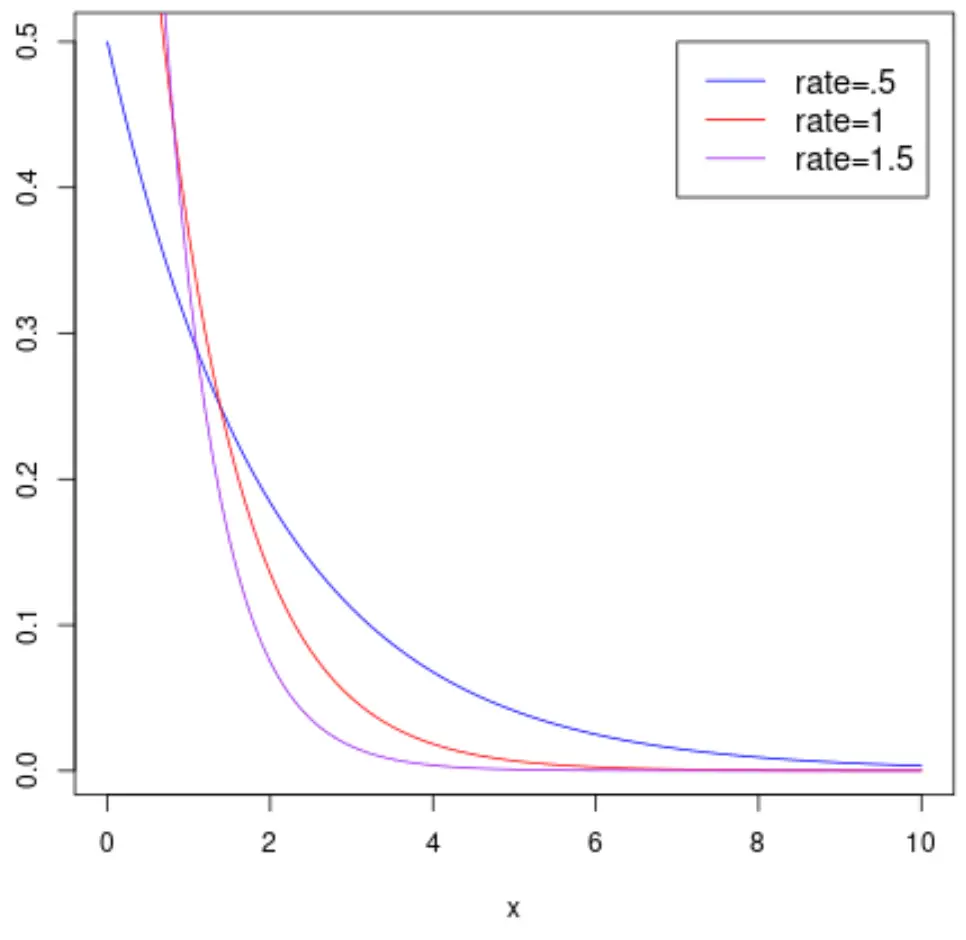
Poniższy wykres przedstawia dystrybuantę zmiennej losowej X , która ma rozkład wykładniczy z różnymi parametrami szybkości:

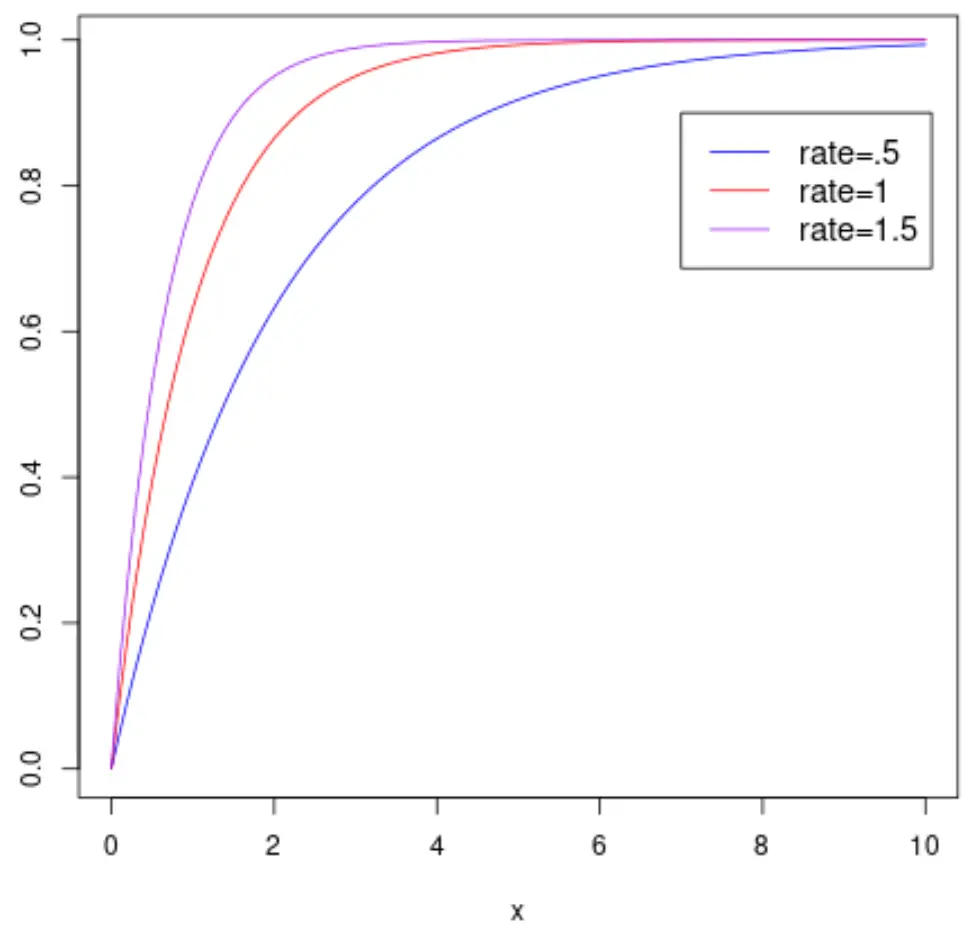
Uwaga: zapoznaj się z tym samouczkiem, aby dowiedzieć się, jak wykreślić rozkład wykładniczy w języku R.

Własności rozkładu wykładniczego

Rozkład wykładniczy ma następujące właściwości:

• Średnia: 1 / λ
• Różnica: 1 / λ ²

Załóżmy na przykład, że średnia liczba minut pomiędzy erupcjami pewnego gejzeru wynosi 40 minut. Obliczylibyśmy współczynnik jako λ = 1/μ = 1/40 = 0,025.

Moglibyśmy następnie obliczyć następujące właściwości tego rozkładu:

• Średni czas oczekiwania na kolejną erupcję: 1/λ = 1 /.025 = 40
• Różnice w czasie oczekiwania na następną erupcję: 1/λ ² = 1 /.025 ² = 1600

Uwaga: Rozkład wykładniczy ma również właściwość bezpamięciową , co oznacza, że wystąpienie zdarzeń przeszłych nie ma wpływu na prawdopodobieństwo wystąpienia przyszłego zdarzenia.

Problemy z praktyką rozkładu wykładniczego

Skorzystaj z poniższych problemów praktycznych, aby sprawdzić swoją wiedzę na temat rozkładu wykładniczego.

Pytanie 1: Nowy klient wchodzi do sklepu średnio co dwie minuty. Po przybyciu klienta określ prawdopodobieństwo, że nowy klient dotrze w czasie krótszym niż minuta.

Rozwiązanie 1: Średni czas między klientami wynosi dwie minuty. Zatem stawkę można obliczyć w następujący sposób:

• λ = 1/µ
• λ = 1/2
• λ = 0,5

Możemy podłączyć λ = 0,5 i x = 1 do wzoru CDF:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0,5(1)
• P(X ≤ 1) = 0,3935

Prawdopodobieństwo, że na przybycie kolejnego klienta będziemy musieli poczekać krócej niż minutę, wynosi 0,3935 .

Pytanie 2: Trzęsienie ziemi występuje w określonym regionie średnio co 400 dni. Po trzęsieniu ziemi określ prawdopodobieństwo, że do następnego trzęsienia ziemi upłynie więcej niż 500 dni.

Rozwiązanie 2: Średni czas między trzęsieniami ziemi wynosi 400 dni. Zatem stawkę można obliczyć w następujący sposób:

• λ = 1/µ
• λ = 1/400
• λ = 0,0025

Możemy podstawić λ = 0,0025 i x = 500 do wzoru CDF:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0,0025(500)
• P(X ≤ 1) = 0,7135

Prawdopodobieństwo, że na kolejne trzęsienie ziemi będziemy musieli poczekać mniej niż 500 dni, wynosi 0,7135. Zatem prawdopodobieństwo, że na kolejne trzęsienie ziemi będziemy musieli poczekać ponad 500 dni, wynosi 1 – 0,7135 = 0,2865 .

Pytanie 3: Call center otrzymuje nowe połączenie średnio co 10 minut. Gdy klient zadzwoni, określ prawdopodobieństwo, że nowy klient zadzwoni w ciągu 10–15 minut.

Rozwiązanie 3: Średni czas pomiędzy połączeniami wynosi 10 minut. Zatem stawkę można obliczyć w następujący sposób:

• λ = 1/µ
• λ = 1/10
• λ = 0,1

Aby obliczyć prawdopodobieństwo, że nowy klient zadzwoni w ciągu 10-15 minut, możemy skorzystać z poniższego wzoru:

• P(10 < X ≤ 15) = (1 – e ^-0,1(15) ) – (1 – e ^-0,1(10) )
• P(10 < X ≤ 15) = 0,7769 – 0,6321
• P(10 < X ≤ 15) = 0,1448

Prawdopodobieństwo, że nowy klient zadzwoni w ciągu 10-15 minut. wynosi 0,1448 .

Dodatkowe zasoby

Poniższe samouczki zawierają wprowadzenie do innych popularnych rozkładów prawdopodobieństwa.

Wprowadzenie do rozkładu normalnego
Wprowadzenie do rozkładu dwumianowego
Wprowadzenie do rozkładu Poissona
Wprowadzenie do jednolitej dystrybucji