Rozkład wykładniczy

Przez Benjamin Anderson 3 sierpnia, 2023 Prawdopodobieństwo 0 komentarzy

W tym artykule wyjaśniono, czym jest rozkład wykładniczy w statystyce i do czego się go wykorzystuje. Znajdziesz tu także właściwości rozkładu wykładniczego, jego wzory, wykres i rozwiązane ćwiczenie. Dodatkowo będziesz w stanie obliczyć dowolne prawdopodobieństwo za pomocą internetowego kalkulatora rozkładu wykładniczego.

Co to jest rozkład wykładniczy?

Rozkład wykładniczy jest ciągłym rozkładem prawdopodobieństwa stosowanym do modelowania czasu oczekiwania na wystąpienie zjawiska losowego.

Dokładniej, rozkład wykładniczy pozwala nam opisać czas oczekiwania między dwoma zdarzeniami, który jest zgodny z rozkładem Poissona. Dlatego rozkład wykładniczy jest ściśle powiązany z rozkładem Poissona.

➤ Zobacz: Co to jest rozkład Poissona?

Rozkład wykładniczy ma charakterystyczny parametr, oznaczony grecką literą λ, który wskazuje, ile razy przewidywane jest wystąpienie badanego zdarzenia w danym okresie.

$X\sim \text{Exp}(\lambda)$

Podobnie rozkład wykładniczy jest również używany do modelowania czasu do wystąpienia awarii. Dlatego rozkład wykładniczy ma kilka zastosowań w teorii niezawodności i przetrwania.

Przykłady rozkładów wykładniczych

Teraz, gdy znamy definicję rozkładu wykładniczego, spójrzmy na kilka przykładów tego typu rozkładu, aby lepiej zrozumieć tę koncepcję.

Przykłady rozkładu wykładniczego:

Czas, jaki upłynął pomiędzy dwoma połączeniami w call center.
Czas, w którym dana osoba musi czekać, aż na określonej ulicy przejedzie bezpłatna taksówka.
Czas oczekiwania na wejście nowego klienta do sklepu.
Czas, jaki upływa pomiędzy wejściem na stronę internetową dwóch różnych użytkowników.
Czas, jaki upłynął na lotnisku od startu jednego samolotu do odlotu drugiego.

Wzór na rozkład wykładniczy

Wzór na funkcję gęstości, który definiuje obliczanie prawdopodobieństwa rozkładu wykładniczego, jest równy λ pomnożonemu przez liczbę e do potęgi ujemnej λ razy x.

Innymi słowy, wzór na obliczenie prawdopodobieństwa rozkładu wykładniczego jest następujący:

👉 Możesz skorzystać z poniższego kalkulatora, aby obliczyć prawdopodobieństwo wystąpienia zmiennej o rozkładzie wykładniczym.

Natomiast wzór na obliczenie skumulowanego prawdopodobieństwa rozkładu wykładniczego jest następujący:

$P[X\leq x]=1-e^{-\lambda x}$

Wykres rozkładu wykładniczego

W tej sekcji można zobaczyć graficzną reprezentację funkcji gęstości i funkcji rozkładu wykładniczego.

Poniżej widać jak zmienia się wykres funkcji gęstości rozkładu wykładniczego w zależności od wartości parametru λ.

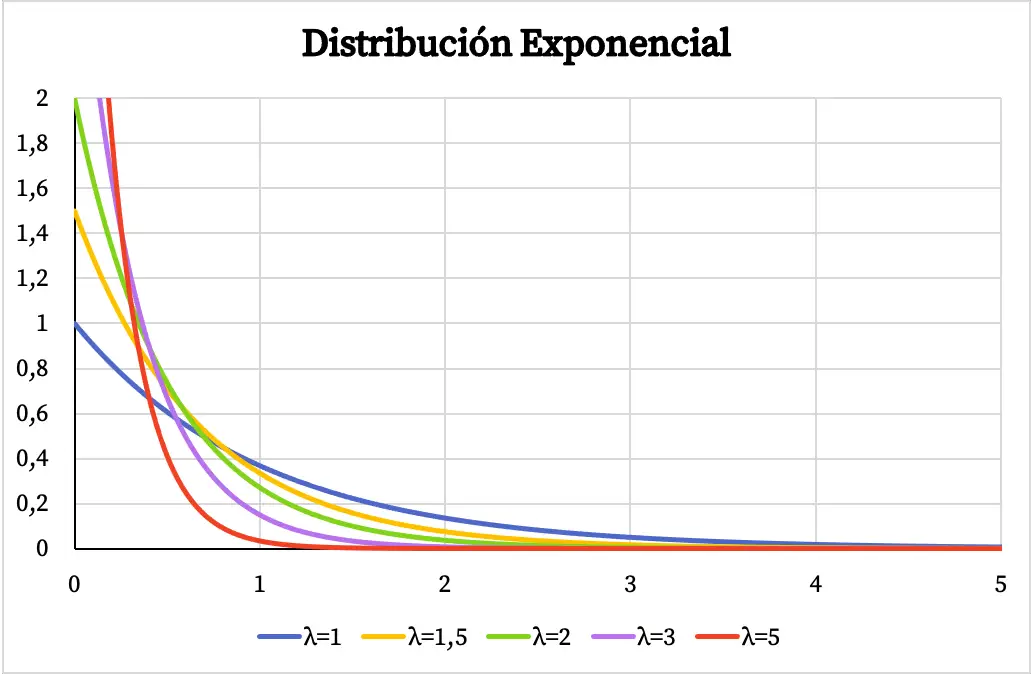
Podobnie skumulowana funkcja prawdopodobieństwa rozkładu wykładniczego zależy również od wartości parametru λ, jak widać na poniższym wykresie:

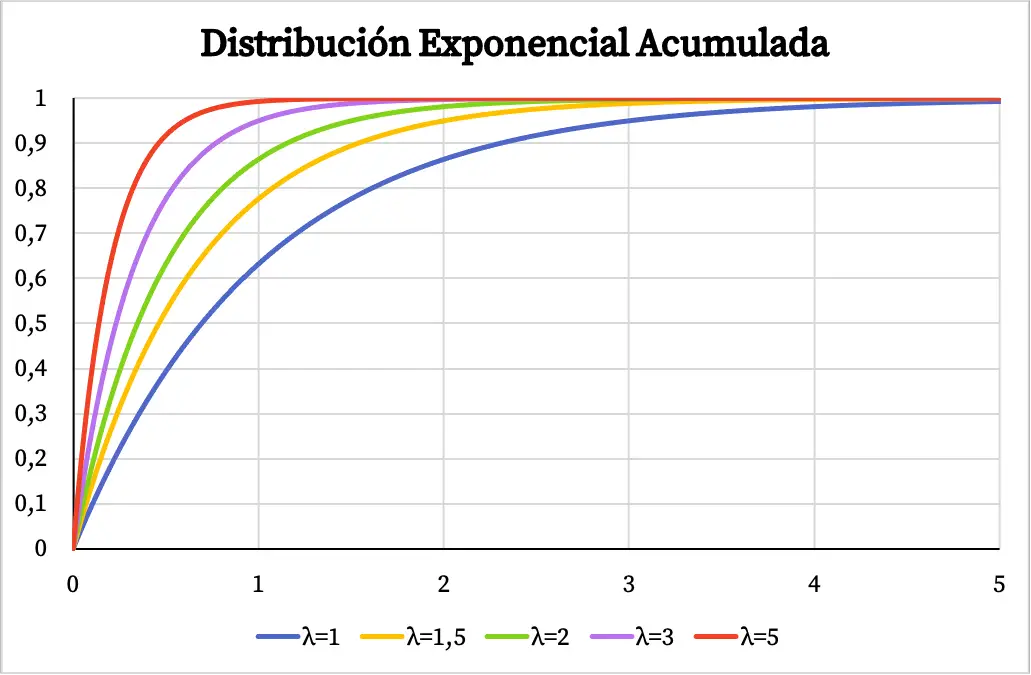
wykres prawdopodobieństwa wykładniczego rozkładu skumulowanego

Rozwiązane ćwiczenie z rozkładu wykładniczego

Średnio λ=1 użytkowników/min uzyskuje dostęp do określonej strony internetowej. Jakie jest prawdopodobieństwo, że czas pomiędzy wejściem dwóch użytkowników wynosi 3 minuty? A prawdopodobieństwo, że będzie ono równe lub mniejsze niż 2 minuty?

Rozkład definiujący zmienną losową tego problemu jest rozkładem wykładniczym, gdyż badamy czas, jaki upływa od momentu wystąpienia zdarzenia (wejścia użytkownika na stronę internetową) do ponownego wystąpienia tego samego zdarzenia.

$X\sim \text{Exp}(1)$

Dlatego też, aby obliczyć prawdopodobieństwo, że czas, jaki upłynął pomiędzy wejściami dwóch różnych użytkowników, wyniesie trzy minuty, należy zastosować wzór na funkcję gęstości (patrz wyżej):

$\begin{aligned}P[X=x]&=\lambda e^{-\lambda x}\\[2ex]P[X=3]&=1\cdot e^{-1\cdot 3}\\[2ex]P[X=3]&=0,05\end{aligned}$

Z drugiej strony, aby wyznaczyć prawdopodobieństwo skumulowane, musimy skorzystać ze wzoru na funkcję rozkładu rozkładu wykładniczego:

$\begin{aligned}P[X\leq x]&=1- e^{-\lambda x}\\[2ex]P[X\leq 2]&=1-e^{-1\cdot 2}\\[2ex]P[X\leq 2]&=0,86\end{aligned}$

Charakterystyka rozkładu wykładniczego

Rozkład wykładniczy ma następujące cechy:

Rozkład wykładniczy ma charakterystyczny parametr λ, który wskazuje, ile razy można spodziewać się wystąpienia badanego zjawiska w danym okresie.

$X\sim \text{Exp}(\lambda)$

Rozkład wykładniczy nie może przyjmować wartości ujemnej, zatem dziedziną rozkładu wykładniczego są wszystkie liczby rzeczywiste większe lub równe zero.

$x\in [0,+\infty)$

Średnia rozkładu wykładniczego jest równa jedności podzielonej przez charakterystyczny parametr λ.

$E[X]=\cfrac{1}{\lambda}$

Wariancja rozkładu wykładniczego jest kwadratem jego średniej, zatem wariancja rozkładu wykładniczego jest równa jedności przez współczynnik λ do kwadratu.

$Var(X)=\cfrac{1}{\lambda^2 }$

Niezależnie od wartości λ, współczynnik asymetrii rozkładu wykładniczego jest zawsze równy 2.

$A=2$

Podobnie współczynnik kurtozy dowolnego rozkładu wykładniczego jest zawsze równy 9.

$C=9$

Wzór na funkcję gęstości rozkładu wykładniczego to:

$P[X=x]=\lambda e^{-\lambda x}$

Natomiast wzór na skumulowaną funkcję prawdopodobieństwa rozkładu wykładniczego jest następujący:

$P[X\leq x]=1-e^{-\lambda x}$

Rozkład wykładniczy jest jednym z niewielu rozkładów prawdopodobieństwa posiadających właściwość braku pamięci. Właściwość ta oznacza, że wystąpienie poprzedniego zdarzenia nie wpływa na prawdopodobieństwo wystąpienia tego zdarzenia w przyszłości. Na przykład w rozkładzie wykładniczym prawdopodobieństwo, że nowy użytkownik uzyska dostęp do strony internetowej w czasie krótszym niż minuta, nie zależy od tego, czy użytkownik właśnie wszedł na stronę, czy też nie wszedł od tego czasu żaden użytkownik. ponad dziesięć minut.

$P[X>x+y|X>y]=P[X>x]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”254″ style=”vertical-align: -5px;”></p> </p> <h2 class=$ Kalkulator rozkładu wykładniczego

Wprowadź wartość parametru λ i wartość x do poniższego kalkulatora, aby obliczyć prawdopodobieństwo. Musisz wybrać prawdopodobieństwo, które chcesz obliczyć i wprowadzić liczby, używając kropki jako separatora dziesiętnego, na przykład 0,50.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej