Co to są zdarzenia rozłączne? (definicja i przykłady)

Zdarzenia rozłączne to zdarzenia, które nie mogą wystąpić w tym samym czasie.

Zapisane w notacji probabilistycznej zdarzenia A i B są rozłączne, jeśli ich przecięcie wynosi zero. Można to zapisać w następujący sposób:

• P(A i B) = 0
• P(A∩B) = 0

Załóżmy na przykład, że wybieramy losowo kartę z talii. Niech zdarzenie A będzie zdarzeniem, w którym kartą będzie pik lub trefl, a zdarzeniem B będzie zdarzeniem, w którym kartą będzie kier lub karo.

Zdefiniowalibyśmy przykładową przestrzeń dla zdarzeń w następujący sposób:

• A = {pik, trefl}
• B = {Serce, Diament}

Należy zwrócić uwagę, że dwie próbkowane przestrzenie nie nakładają się na siebie. Zatem zdarzenia A i B są zdarzeniami rozłącznymi, ponieważ oba nie mogą wystąpić w tym samym czasie.

Uwaga: Mówi się również, że zdarzenia rozłączne wzajemnie się wykluczają .

Przykłady zdarzeń rozłącznych

Oto kilka przykładów rozłącznych wydarzeń.

Przykład 1: losowanie

Załóżmy, że rzucasz monetą. Niech zdarzenie A będzie zdarzeniem, w którym moneta wyląduje na orle, a zdarzenie B będzie zdarzeniem, w którym moneta wyląduje na orle.

Zdarzenie A i zdarzenie B byłyby rozłączne, ponieważ nie mogły wystąpić jednocześnie. Moneta nie może wylądować na orle ani reszce.

Przykład 2: rzucanie kostkami

Załóżmy, że rzucasz kostką. Niech zdarzenie A będzie zdarzeniem, w którym kość wyląduje na liczbie nieparzystej i niech zdarzenie B będzie zdarzeniem, w którym kość wyląduje na liczbie parzystej.

Zdarzenie A i zdarzenie B byłyby rozłączne, ponieważ nie mogły wystąpić jednocześnie. Kości nie mogą spaść na liczbę parzystą i nieparzystą.

Przykład 3: Lokalizacja Pro Bowl

Załóżmy, że liga NFL chce wybrać lokalizację na organizację meczu Pro Bowl. Zawęzili opcje w Miami i San Diego. Umieszczają oba imiona w kapeluszu i wybierają jedno losowo. Załóżmy, że wydarzenie A to wydarzenie, na które wybrali Miami, a wydarzenie B to wydarzenie, na które wybrali San Diego.

Zdarzenie A i zdarzenie B byłyby rozłączne, ponieważ nie mogły wystąpić jednocześnie. Nie można wybrać Miami i San Diego.

Zobacz rozłączne zdarzenia

Przydatnym sposobem wizualizacji zdarzeń rozłącznych jest utworzenie diagramu Venna.

Jeśli dwa zdarzenia są rozłączne , na diagramie Venna w ogóle nie będą się nakładać:

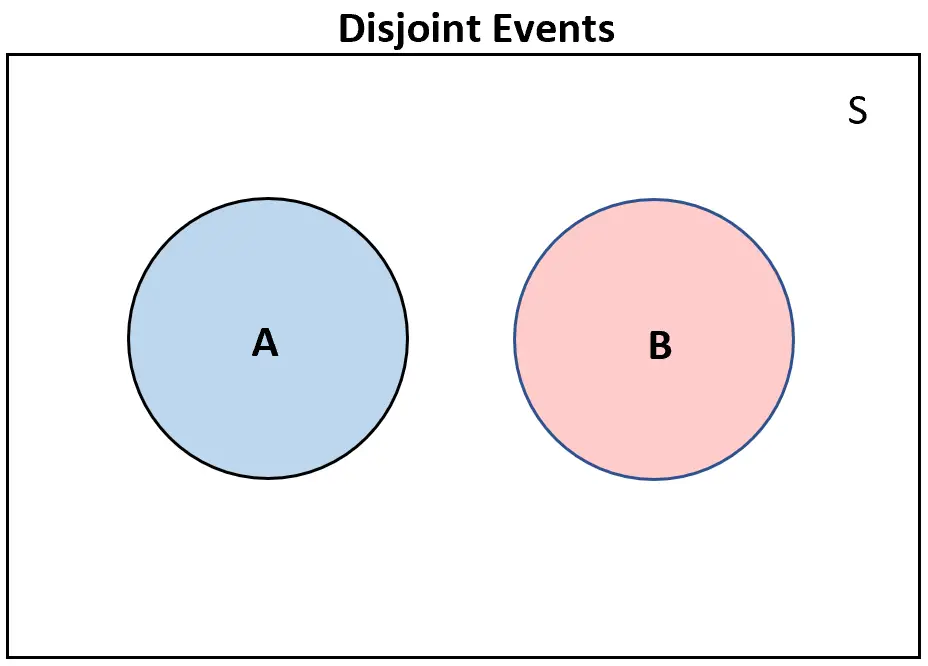
I odwrotnie, jeśli dwa zdarzenia nie są rozłączne , na diagramie Venna będzie przynajmniej w pewnym stopniu nakładać się:

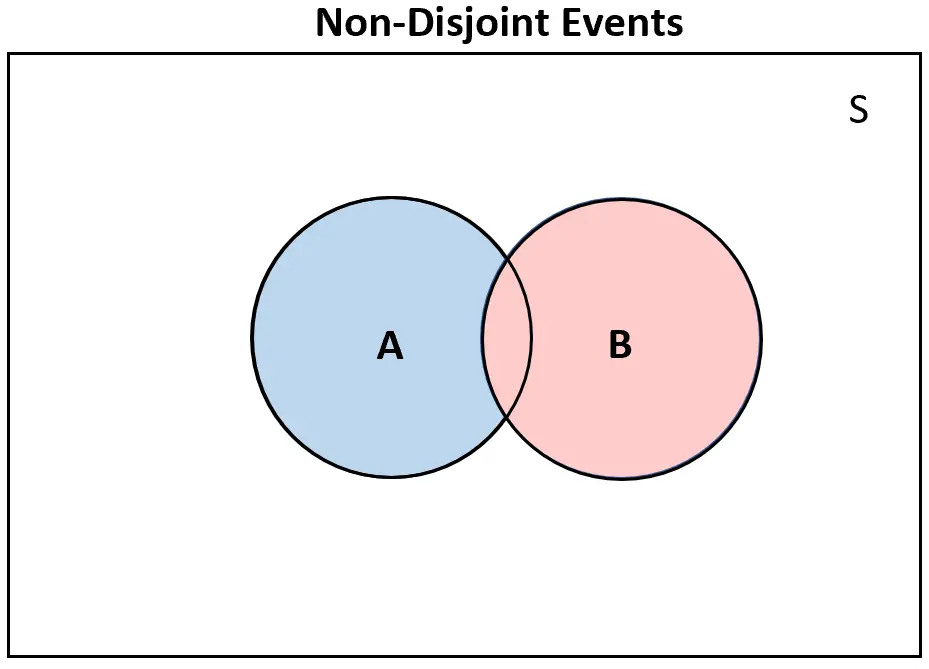
Prawdopodobieństwo zdarzeń rozłącznych

Jak wspomniano wcześniej, jeśli dwa zdarzenia są rozłączne, prawdopodobieństwo ich wystąpienia w tym samym czasie wynosi zero.

• P(A∩B) = 0

Podobnie prawdopodobieństwo wystąpienia dowolnego zdarzenia można obliczyć, dodając ich indywidualne prawdopodobieństwa.

• P(A∪B) = P(A) + P(B)

Na przykład, niech zdarzenie A będzie zdarzeniem, w którym kość wypadnie na 1 lub 2, i niech zdarzenie B będzie zdarzeniem, w którym kość wypadnie na 5 lub 6.

Zdefiniowalibyśmy przykładową przestrzeń dla zdarzeń w następujący sposób:

• ZA = {1, 2}
• B = {5, 6}

Obliczylibyśmy prawdopodobieństwo wystąpienia zdarzenia A lub zdarzenia B jako:

• P(A∪B) = P(A) + P(B)
• P(A∪B) = 2/6 + 2/6
• P(A∪B) = 4/6 = 2/3

Prawdopodobieństwo wystąpienia zdarzenia A lub zdarzenia B wynosi 2/3 .

Dodatkowe zasoby

Poniższe samouczki zawierają wyjaśnienia innych typowych tematów dotyczących prawdopodobieństwa:

Jak znaleźć prawdopodobieństwo A lub B: z przykładami
Jak znaleźć prawdopodobieństwo A i B: z przykładami
Prawo prawdopodobieństwa całkowitego: definicja i przykłady