Schemat kołowy

W tym artykule dowiesz się, czym jest wykres kołowy, jak zbudować wykres kołowy oraz krok po kroku wykonać ćwiczenie dla tego typu wykresu. Ponadto będziesz mógł zobaczyć, jakie są cechy wykresów kołowych.

Co to jest wykres kołowy?

Wykres kołowy , zwany także wykresem kołowym , to rodzaj wykresu statystycznego służącego do wizualnego przedstawienia wartości procentowych i proporcji. Dokładniej, na wykresie kołowym dane są reprezentowane przez fragmenty koła, tak że kąt każdego sera jest proporcjonalny do jego częstotliwości.

Dlatego im wyższa częstotliwość wartości, tym większy udział zajmuje ona na wykresie kołowym.

W statystyce wykresy kołowe są bardzo przydatne do przedstawiania danych jakościowych na wykresie, a także pozwalają na szybkie wyciąganie wniosków.

Należy zauważyć, że wykres kołowy ma wiele różnych nazw, takich jak wykres kołowy, wykres pizzy, wykres kołowy, wykres sera, a nawet wykres 360 stopni.

Jak zrobić wykres kołowy

Biorąc pod uwagę definicję wykresu kołowego, w tej sekcji pokazano, jak utworzyć wykres tego typu:

1. Zbierz dane statystyczne i przygotuj odpowiednią tabelę częstości.
2. Oblicz kąt każdego sektora wykresu, korzystając z poniższego wzoru



Złoto



jest kątem sektora i ,



jego częstotliwość bezwzględna i



całkowita liczba danych.

3. Na podstawie obliczonych kątów przedstaw sektory na wykresie kołowym za pomocą kątomierza.
4. Oblicz procent każdego sektora za pomocą następującego wzoru:



Złoto



jest procentem sektora i ,



jego częstotliwość bezwzględna i



całkowita liczba danych.

5. Wskaż na wykresie procent każdego sektora.

Przykład wykresu kołowego

Abyś mógł zobaczyć, jak zbudowany jest wykres kołowy, zostawiam Cię z przykładem wyjaśnionym krok po kroku poniżej.

• 50 osób zapytano o ulubione miasto, a dane zestawiono w poniższej tabeli. Przedstaw te dane statystyczne na wykresie kołowym.

Przede wszystkim musisz znaleźć kąt odpowiadający każdemu serowi . W tym celu stosujemy następujący wzór:

Przykładowo obliczany jest kąt odpowiadający pierwszej wartości w tabeli danych:

Kiedy już znamy kąt, po prostu przedstawmy sektor kołowy za pomocą kątomierza:

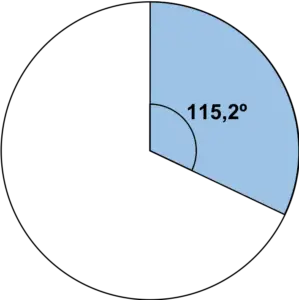
Powtarzamy ten sam krok dla wszystkich wartości w tabeli:

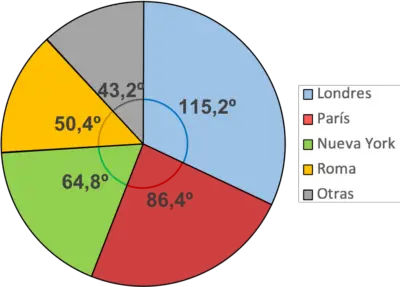
Zaleca się pomalowanie każdego sektora na kolor, aby ułatwić zrozumienie wykresu. Podobnie powinieneś dodać legendę, aby pokazać znaczenie każdego koloru na diagramie.

Po narysowaniu wykresu serów musimy obliczyć procent każdego sera, aby umieścić go na wykresie. Aby to zrobić, używamy następującej formuły:

Procent każdego sektora wynosi zatem:

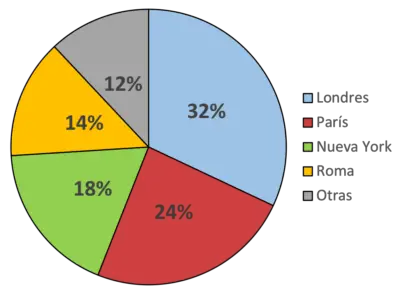
Za pomocą tego wykresu kołowego wskazujemy, że na przykład kolor niebieski reprezentuje Londyn i jest miejscem preferowanym przez większość ludzi (32% osób). Z kolei kolor zielony reprezentuje Nowy Jork, który jest ulubionym miastem 18% ankietowanych.

Funkcje wykresu kołowego

Charakterystyka Camemberta jest następująca:

• Wykres kołowy jest bardzo przydatny do przedstawiania danych jakościowych.
• Istnieją jednak inne typy wykresów statystycznych, które lepiej nadają się do przedstawiania zmiennych ilościowych lub szeregów czasowych.
• Ponadto na wykresie kołowym można przedstawić tylko jedną zmienną, co utrudnia porównywanie zmiennych.
• Wykres kołowy jest bardzo wizualny, co pozwala na szybką analizę i wnioski.
• Odczytywanie wykresu jest trudne, gdy sektorów jest wiele lub niektóre są bardzo małe. W takim przypadku zaleca się zgrupowanie małych sektorów w jeden sektor zwany „Innymi”.