Jak interpretować wykresy diagnostyczne w r

Modele regresji liniowej służą do opisu związku pomiędzy jedną lub większą liczbą zmiennych predykcyjnych a zmienną odpowiedzi.

Jednakże po dopasowaniu modelu regresji dobrym pomysłem jest utworzenie również wykresów diagnostycznych w celu analizy reszt modelu i upewnienia się, że model liniowy jest odpowiedni do zastosowania w przypadku konkretnych danych, z którymi pracujemy.

W tym samouczku wyjaśniono, jak tworzyć i interpretować wykresy diagnostyczne dla danego modelu regresji w języku R.

Przykład: Tworzenie i interpretowanie wykresów diagnostycznych w R

Załóżmy, że dopasowujemy prosty model regresji liniowej, wykorzystując „przepracowane godziny” do przewidywania „ocen z egzaminu” uczniów w określonej klasie:

 #create data frame
df <- data. frame (hours=c(1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6),
                 score=c(67, 65, 68, 77, 73, 79, 81, 88, 80, 67, 84, 93, 90, 91)) 

#fit linear regression model
model = lm(score ~ hours, data=df)

Możemy użyć polecenia plot() , aby utworzyć cztery wykresy diagnostyczne dla tego modelu regresji:

 #produce diagnostic plots for regression model
plot(model)

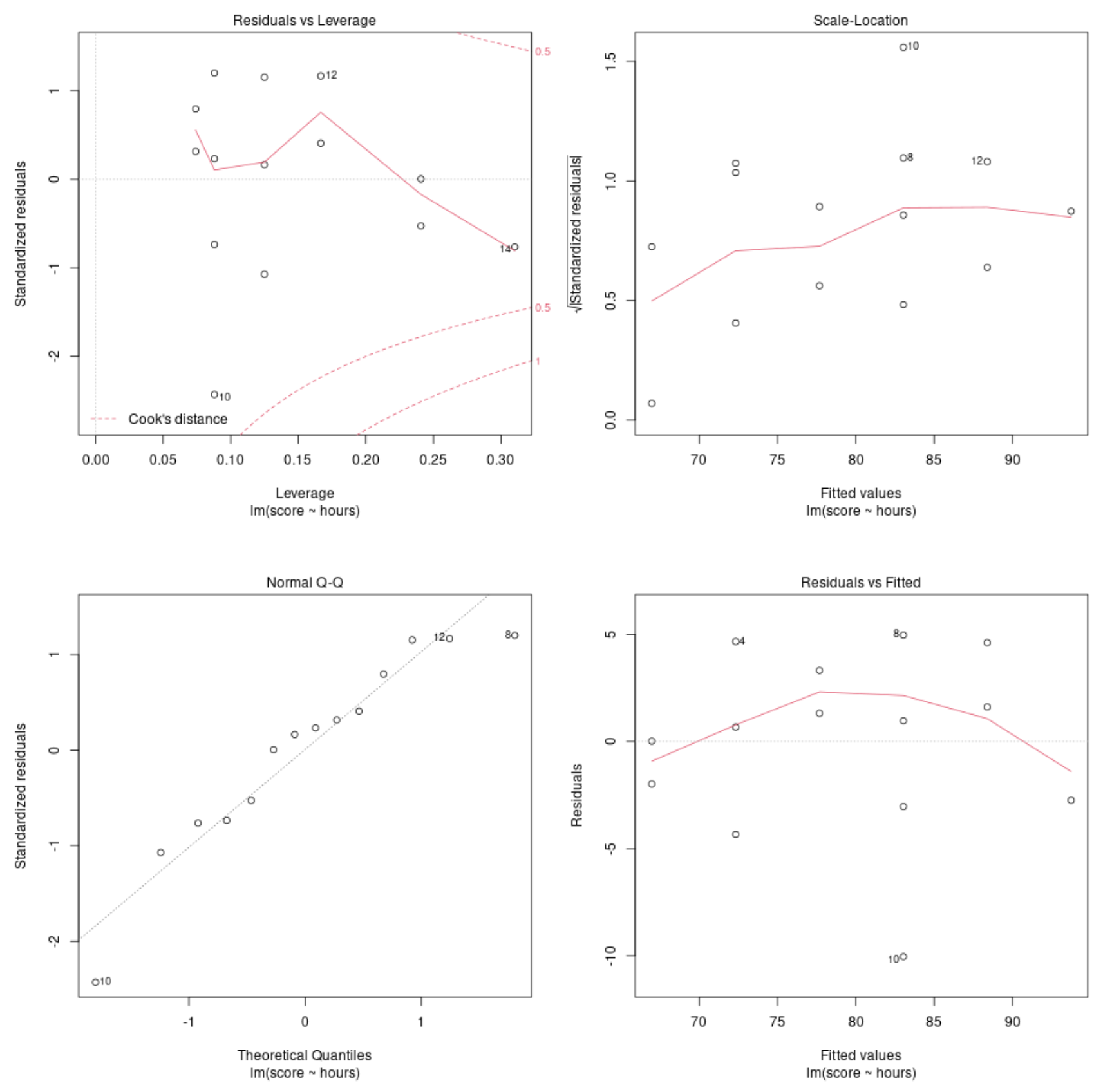
Wykres diagnostyczny nr 1: Pozostałości vs. Wykres dźwigni

Wykres ten służy do identyfikowania wpływowych obserwacji. Jeśli jakiekolwiek punkty na tym wykresie znajdują się poza odległością Cooka (linie przerywane), jest to istotna obserwacja.

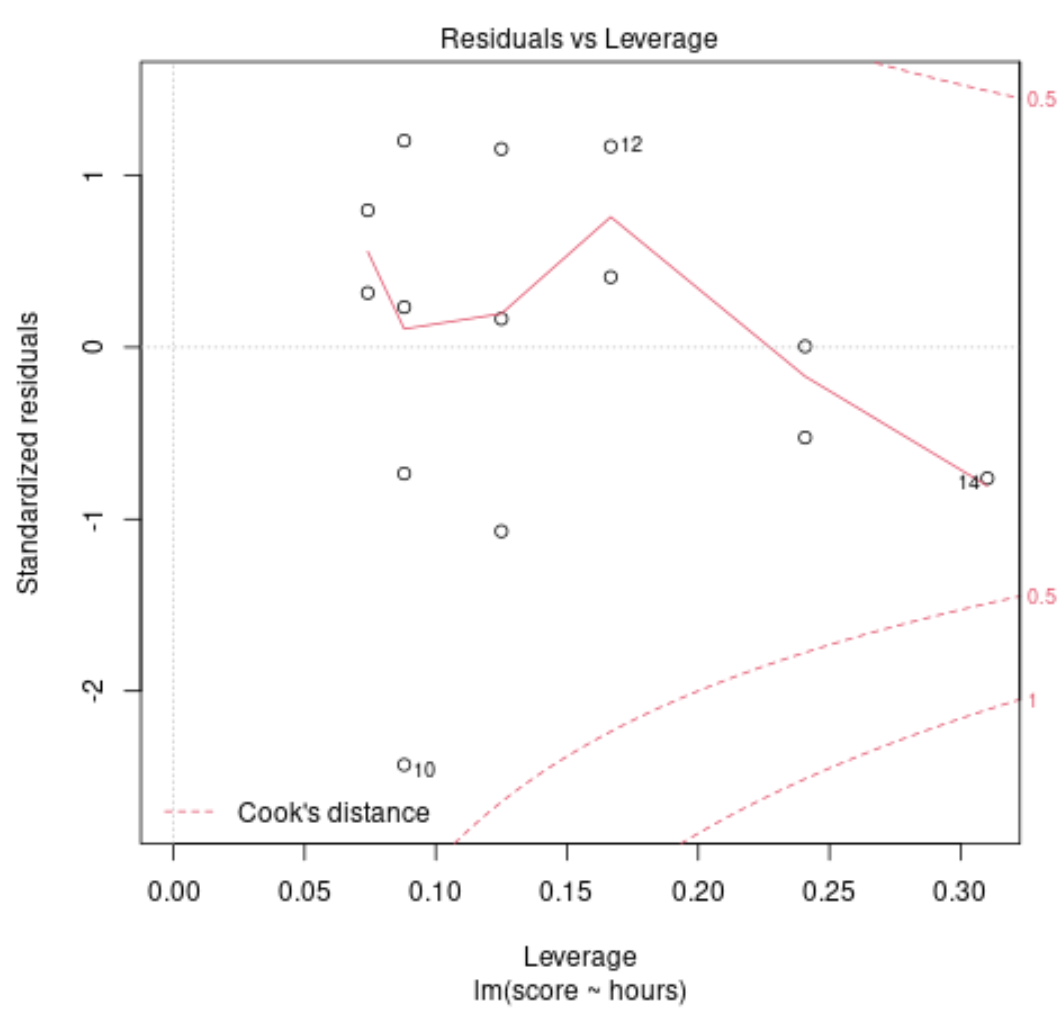
W naszym przykładzie widzimy, że obserwacja nr 10 jest najbliższa granicy odległości Cooka, ale nie wykracza poza linię przerywaną. Oznacza to, że w naszym zbiorze danych nie ma punktów o zbyt dużym wpływie.

Wykres diagnostyczny nr 2: Wykres skali i lokalizacji

Wykres ten służy do weryfikacji założenia o równości wariancji (zwanej także „homoskedastycznością”) wśród reszt naszego modelu regresji. Jeśli czerwona linia jest w przybliżeniu pozioma na wykresie, wówczas prawdopodobnie spełnione jest założenie o równej wariancji.

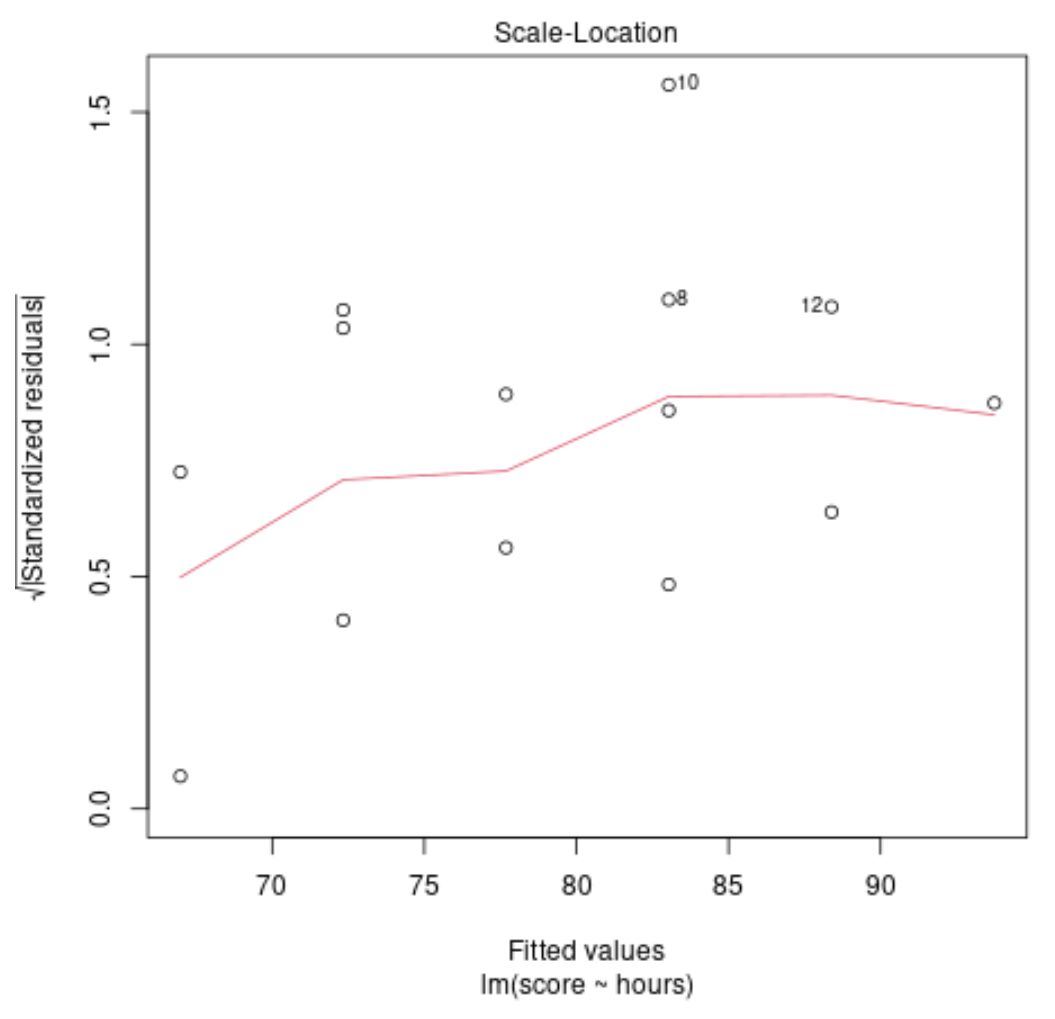
W naszym przykładzie widzimy, że czerwona linia nie jest dokładnie pozioma na wykresie, ale w żadnym punkcie nie odchyla się zbyt mocno. Prawdopodobnie stwierdzamy, że założenie o równej wariancji nie jest w tym przypadku naruszone.

Powiązane: Zrozumienie heteroskedastyczności w analizie regresji

Ślad diagnostyczny nr 3: normalny ślad QQ

Wykres ten służy do określenia, czy reszty z modelu regresji mają rozkład normalny. Jeżeli punkty na tym wykresie leżą w przybliżeniu na prostej ukośnej, to możemy założyć, że reszty mają rozkład normalny.

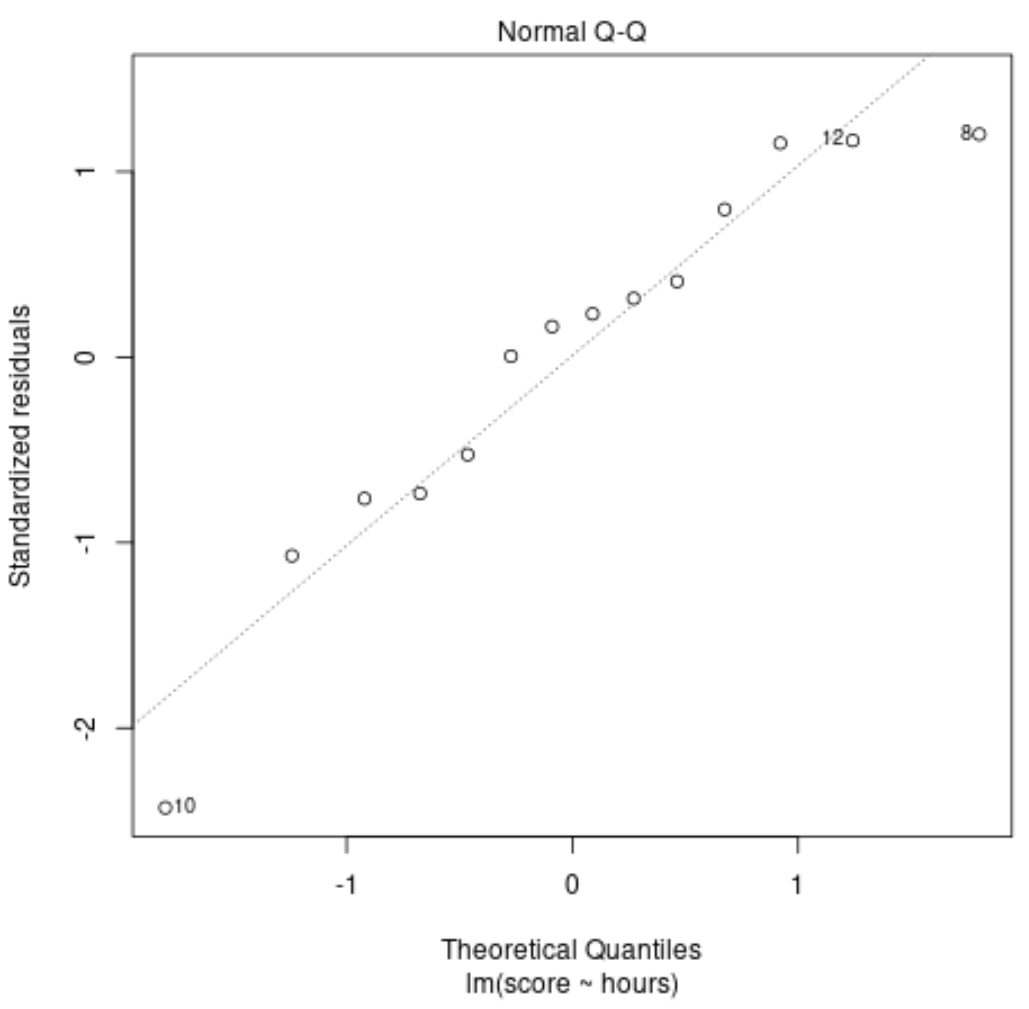
W naszym przykładzie widzimy, że punkty leżą mniej więcej na ukośnej linii prostej. Obserwacje #10 i #8 odbiegają nieco od linii na końcach, ale nie na tyle, aby stwierdzić, że reszty nie mają rozkładu normalnego.

Wykres diagnostyczny nr 4: Pozostałości vs. Dostosowana fabuła

Wykres ten służy do określenia, czy reszty wykazują wzory nieliniowe. Jeśli czerwona linia na środku wykresu jest w przybliżeniu pozioma, możemy założyć, że reszty układają się według wzoru liniowego.

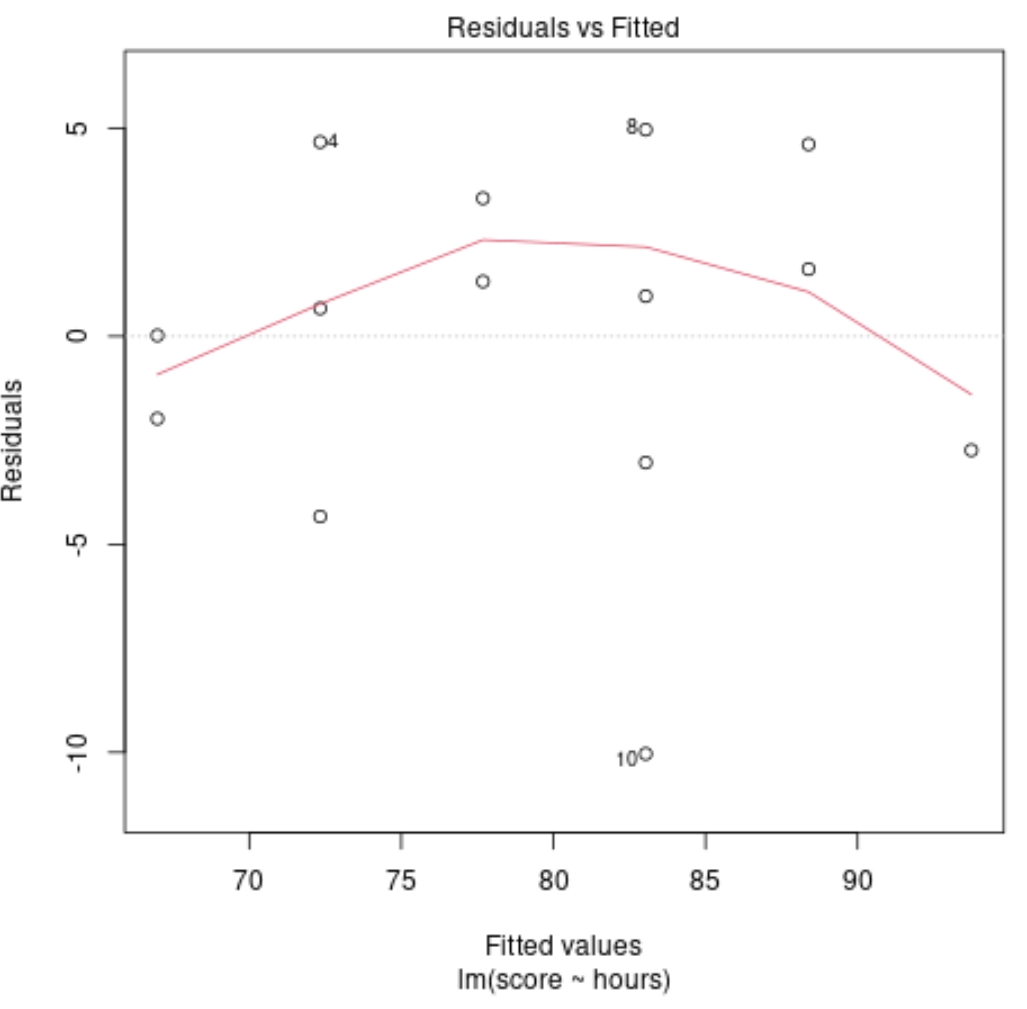
W naszym przykładzie widzimy, że czerwona linia odbiega od idealnej linii poziomej, ale nie znacząco. Prawdopodobnie stwierdzimy, że reszty mają w przybliżeniu liniowy wzór i że dla tego zbioru danych odpowiedni jest model regresji liniowej.

Dodatkowe zasoby

Cztery założenia regresji liniowej
Czym są reszty w statystyce?
Jak utworzyć wykres rezydualny w R
Jak interpretować skalę i wykres lokalizacyjny