Co to jest silnia anova? (definicja – przykład)

Czynnikowa analiza ANOVA to dowolna analiza ANOVA („analiza wariancji”), która wykorzystuje dwa lub więcej niezależnych czynników i jedną zmienną odpowiedzi.

Tego typu ANOVA należy używać zawsze, gdy chcesz zrozumieć, jak dwa lub więcej czynników wpływana zmienną odpowiedzi i czy istnieje efekt interakcji między czynnikami na zmienną odpowiedzi.

W tym samouczku przedstawiono kilka przykładów sytuacji, w których można zastosować silniową analizę ANOVA, a także przykład krok po kroku sposobu przeprowadzenia silniowej analizy ANOVA.

Uwaga: Dwuczynnikowa ANOVA jest rodzajem silniowej ANOVA.

Przykłady zastosowania silniowej ANOVA

Czynniczą ANOVA można zastosować w każdej z następujących sytuacji.

Przykład 1: Wzrost roślin

Botanik chce zrozumieć, jak ekspozycja na słońce i częstotliwość podlewania wpływają na wzrost roślin. Sadzi 100 nasion i pozwala im rosnąć przez trzy miesiące w różnych warunkach nasłonecznienia i częstotliwości podlewania. Po trzech miesiącach rejestruje wysokość każdej rośliny.

W tym przypadku ma następujące zmienne:

• Zmienna odpowiedzi: wzrost roślin
• Czynniki: ekspozycja na słońce, częstotliwość podlewania

I chciałaby odpowiedzieć na następujące pytania:

• Czy ekspozycja na słońce wpływa na wzrost roślin?
• Czy częstotliwość podlewania wpływa na wzrost roślin?
• Czy istnieje efekt interakcji pomiędzy ekspozycją na słońce a częstotliwością podlewania?

Może zastosować do tej analizy silniową analizę wariancji, ponieważ chce zrozumieć, w jaki sposób dwa czynniki wpływają na pojedynczą zmienną odpowiedzi.

Przykład 2: Wyniki egzaminu

Profesor chce zrozumieć, jak czas zajęć i metoda nauczania wpływają na wyniki egzaminu. Wykorzystuje dwie różne metody nauczania i dwa różne pory nauczania (wczesnym rankiem i wczesnym popołudniem), a na koniec semestru rejestruje średnie wyniki egzaminów każdego studenta.

W tym przypadku ma następujące zmienne:

• Zmienna odpowiedzi: wynik egzaminu
• Czynniki: metoda nauczania, czas nauczania

I chciałby odpowiedzieć na następujące pytania:

• Czy metoda nauczania wpływa na wyniki egzaminu?
• Czy czas nauczania wpływa na wyniki egzaminu?
• Czy istnieje efekt interakcji pomiędzy metodą nauczania a czasem nauczania?

Mógłby zastosować do tej analizy silniową analizę wariancji, ponieważ chce zrozumieć, w jaki sposób dwa czynniki wpływają na pojedynczą zmienną odpowiedzi.

Przykład 3: Dochód roczny

Ekonomista zbiera dane, aby zrozumieć, jak poziom wykształcenia (magisterium, dyplom ukończenia studiów, stopień magistra), stan cywilny (panny, rozwiedziony, żonaty) i region (północ, wschód, południe, zachód) wpływają na roczny dochód.

W tym przypadku ma następujące zmienne:

• Zmienna odpowiedzi: roczny dochód
• Czynniki: poziom wykształcenia, stan cywilny, region

I chciałby odpowiedzieć na następujące pytania:

• Czy poziom wykształcenia wpływa na dochody?
• Czy stan cywilny wpływa na dochody?
• Czy region wpływa na dochody?
• Czy istnieje efekt interakcji pomiędzy tymi trzema niezależnymi czynnikami?

Mógłby zastosować do tej analizy silniową analizę wariancji, ponieważ chce zrozumieć, w jaki sposób trzy czynniki wpływają na pojedynczą zmienną odpowiedzi.

Przykład silni ANOVA krok po kroku

Botanik chce wiedzieć, czy ekspozycja na światło słoneczne i częstotliwość podlewania wpływają na wzrost roślin. Sadzi 40 nasion i pozwala im rosnąć przez dwa miesiące w różnych warunkach nasłonecznienia i częstotliwości podlewania. Po dwóch miesiącach rejestruje wysokość każdej rośliny.

Wyniki przedstawiono poniżej:

Widzimy, że w każdej kombinacji warunków wyhodowano pięć roślin.

Na przykład pięć roślin uprawiano przy codziennym podlewaniu i bez światła słonecznego, a ich wysokość po dwóch miesiącach wynosiła 4,8 cala, 4,4 cala, 3,2 cala, 3,9 cala i 4,4 cala:

Botanik wykorzystuje te dane do przeprowadzenia silniowej analizy ANOVA w programie Excel i otrzymuje następujący wynik:

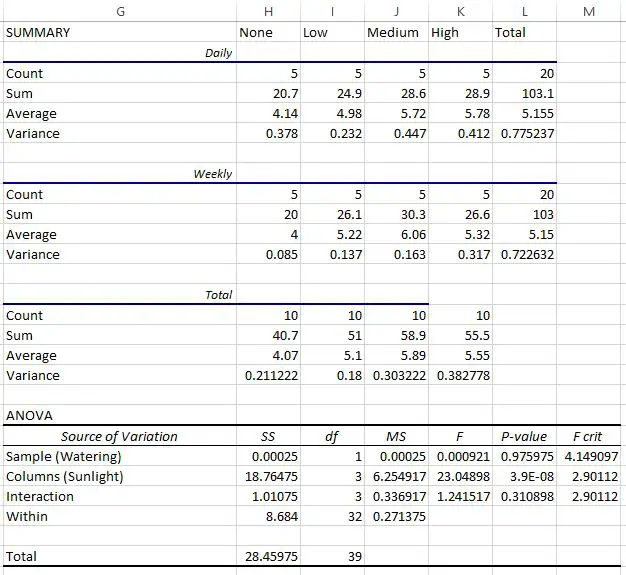
Ostatnia tabela przedstawia wynik silni ANOVA:

• Wartość p dla interakcji pomiędzy częstotliwością podlewania a ekspozycją na słońce wyniosła 0,310898 . Nie jest to statystycznie istotne na poziomie alfa 0,05.
• Wartość p dla częstotliwości nawadniania wyniosła 0,975975 . Nie jest to statystycznie istotne na poziomie alfa 0,05.
• Wartość p dla ekspozycji na słońce wyniosła 3,9E-8 (0,000000039) . Jest to statystycznie istotne na poziomie alfa 0,05.

Można stwierdzić, że ekspozycja na światło słoneczne jest jedynym czynnikiem mającym statystycznie istotny wpływ na wzrost roślin.

Można również stwierdzić, że nie ma związku pomiędzy ekspozycją na słońce a częstotliwością podlewania i że częstotliwość podlewania nie ma statystycznie istotnego wpływu na wzrost roślin. rośliny.

Dodatkowe zasoby

Poniższe tutoriale dostarczają dodatkowych informacji o modelach ANOVA:

Wprowadzenie do jednokierunkowej ANOVA
Wprowadzenie do dwukierunkowej ANOVA
Wprowadzenie do powtarzanych pomiarów ANOVA
Różnice między ANOVA, ANCOVA, MANOVA i MANCOVA