Skumulowana częstotliwość względna

W tym artykule wyjaśniono, jaka jest skumulowana częstotliwość względna w statystykach. Znajdziesz więc definicję skumulowanej częstotliwości względnej, sposób uzyskania skumulowanej częstotliwości względnej oraz dwa ćwiczenia rozwiązane krok po kroku.

Co to jest skumulowana częstotliwość względna?

W statystyce skumulowana częstotliwość względna jest skumulowaną sumą częstotliwości względnych. Oznacza to, że skumulowana częstotliwość względna wartości jest równa częstotliwości względnej tej wartości plus częstotliwości względne wszystkich wartości mniejszych od niej.

Symbolem skumulowanej częstotliwości względnej jest H _i . Jednak w statystyce nie ma jeszcze pełnego konsensusu co do symbolu tego typu częstotliwości, dlatego też można go wyrazić za pomocą innego symbolu.

Oczywiście, aby zrozumieć znaczenie skumulowanej częstotliwości względnej, musisz najpierw mieć jasność co do pojęcia częstotliwości względnej, dlatego przed kontynuowaniem wyjaśnień polecam odwiedzić poniższy link:

Jak obliczyć skumulowaną częstotliwość względną

Aby obliczyć skumulowaną częstotliwość względną, należy wykonać następujące kroki:

1. Utwórz tabelę częstości ze wszystkimi różnymi wartościami z próbki statystycznej.
2. Oblicz częstotliwość bezwzględną każdej wartości.
3. Na podstawie częstotliwości bezwzględnych określ częstotliwość względną każdej wartości.
4. Znajdź skumulowaną częstotliwość względną każdej wartości, którą oblicza się, dodając częstotliwość względną samej wartości oraz częstotliwości względne wszystkich mniejszych wartości.

Pamiętaj, że jeśli chcesz obliczyć skumulowany procent częstotliwości względnej , czyli skumulowaną częstotliwość względną wyrażoną w procentach, wystarczy wykonać te same kroki i pomnożyć wyniki przez 100.

Przykłady skumulowanej częstotliwości względnej

Aby można było zobaczyć, jak obliczana jest skumulowana częstotliwość względna, poniżej pokazano dwa przykłady rozwiązane krok po kroku. W pierwszym przykładzie znajdujemy skumulowaną częstotliwość względną zmiennej dyskretnej, a w drugim przykładzie zmienną ciągłą, ponieważ proces ten nieznacznie się różni.

Przykład 1: zmienna dyskretna

• Oceny uzyskane z przedmiotu statystyka w klasie 30 uczniów przedstawiają się następująco. Jaka jest skumulowana względna częstotliwość każdej nuty?

W tym przypadku zmienna jest dyskretna, ponieważ nie może przyjmować wartości dziesiętnej. Nie jest zatem konieczne grupowanie danych według przedziałów, ale obliczenia można wykonać bezpośrednio.

Dlatego sporządzamy tabelę częstości i określamy częstotliwość bezwzględną każdej innej wartości:

Następnie obliczamy względną częstotliwość każdej wartości (jak to się robi, możesz zobaczyć w linku na początku postu).

Kiedy obliczymy częstotliwość bezwzględną i częstotliwość względną zbioru danych, możemy uzyskać skumulowaną częstotliwość względną. Aby to zrobić, musimy dodać częstotliwość względną danej wartości plus wszystkie poprzednie częstotliwości względne lub, innymi słowy, poprzednią skumulowaną częstotliwość względną:

W skrócie, tabela częstotliwości z częstotliwością bezwzględną, częstotliwością względną i skumulowaną częstotliwością względną wygląda następująco:

Pamiętaj, że ostatnia wartość skumulowanej częstotliwości względnej powinna zawsze wynosić 1. Jeśli otrzymasz inną liczbę, oznacza to, że popełniłeś błąd w obliczeniach.

Przykład 2: zmienna ciągła

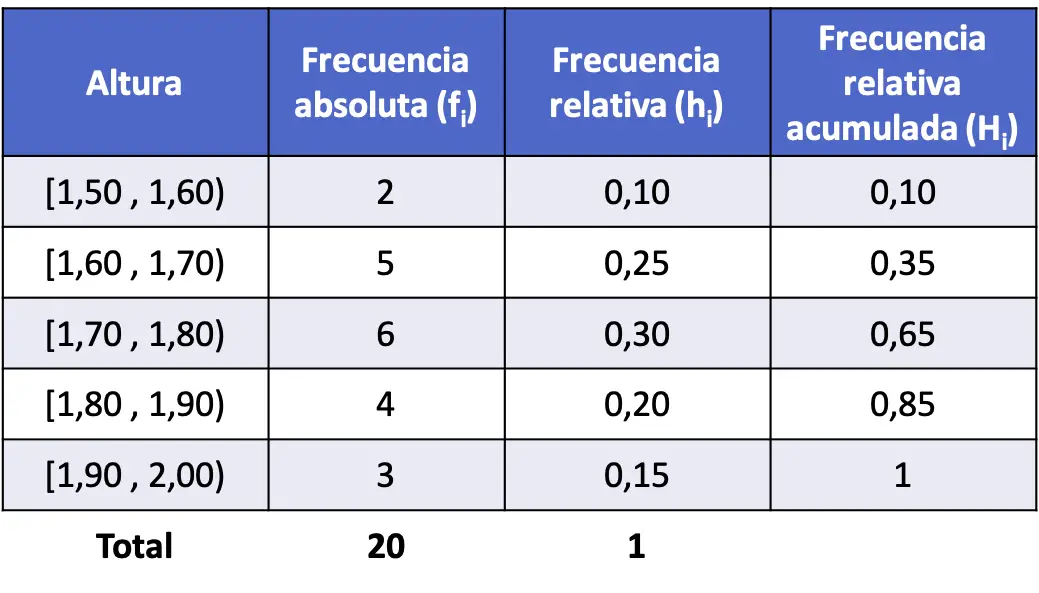
• Zmierzono wzrost 20 osób i uzyskano wyniki podane poniżej. Podziel dane na przedziały i znajdź skumulowaną względną częstotliwość każdego przedziału.

Ten przypadek różni się od poprzedniego problemu, ponieważ liczby są dziesiętne, co oznacza, że zmienna może przyjmować dowolną wartość i dlatego jest ciągła. Dlatego utworzymy tabelę częstości, grupując dane w przedziały.

Dlatego konstruujemy tabelę i uzyskujemy bezwzględną częstotliwość każdego przedziału:

Teraz obliczamy częstotliwości względne, dzieląc częstotliwość bezwzględną każdego przedziału przez całkowitą liczbę punktów danych:

I na koniec znajdujemy skumulowane częstotliwości względne wszystkich przedziałów. Tak jak poprzednio, aby wyznaczyć skumulowaną częstotliwość względną przedziału, należy dodać częstotliwość względną tego przedziału plus poprzednie częstotliwości względne:

Skumulowana częstotliwość względna i skumulowana częstotliwość bezwzględna

Właśnie widzieliśmy, jak skumulowana częstotliwość względna jest wyprowadzana z częstotliwości względnej. Jednakże ten typ częstotliwości można również znaleźć za pomocą skumulowanej częstotliwości bezwzględnej.

Skumulowaną częstotliwość względną można obliczyć, dzieląc skumulowaną częstotliwość bezwzględną przez całkowitą liczbę danych w próbce.

Dlatego wzór na skumulowaną częstotliwość względną jest następujący:

Złoto:

• 

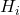
  jest skumulowaną częstotliwością względną.

• 

  jest skumulowaną częstotliwością bezwzględną .

• 

  to całkowita liczba danych.

Zgodnie z pierwszym przykładem przedstawionym powyżej, poniżej przedstawiono sposób obliczania skumulowanej częstotliwości względnej na podstawie skumulowanej częstotliwości bezwzględnej:

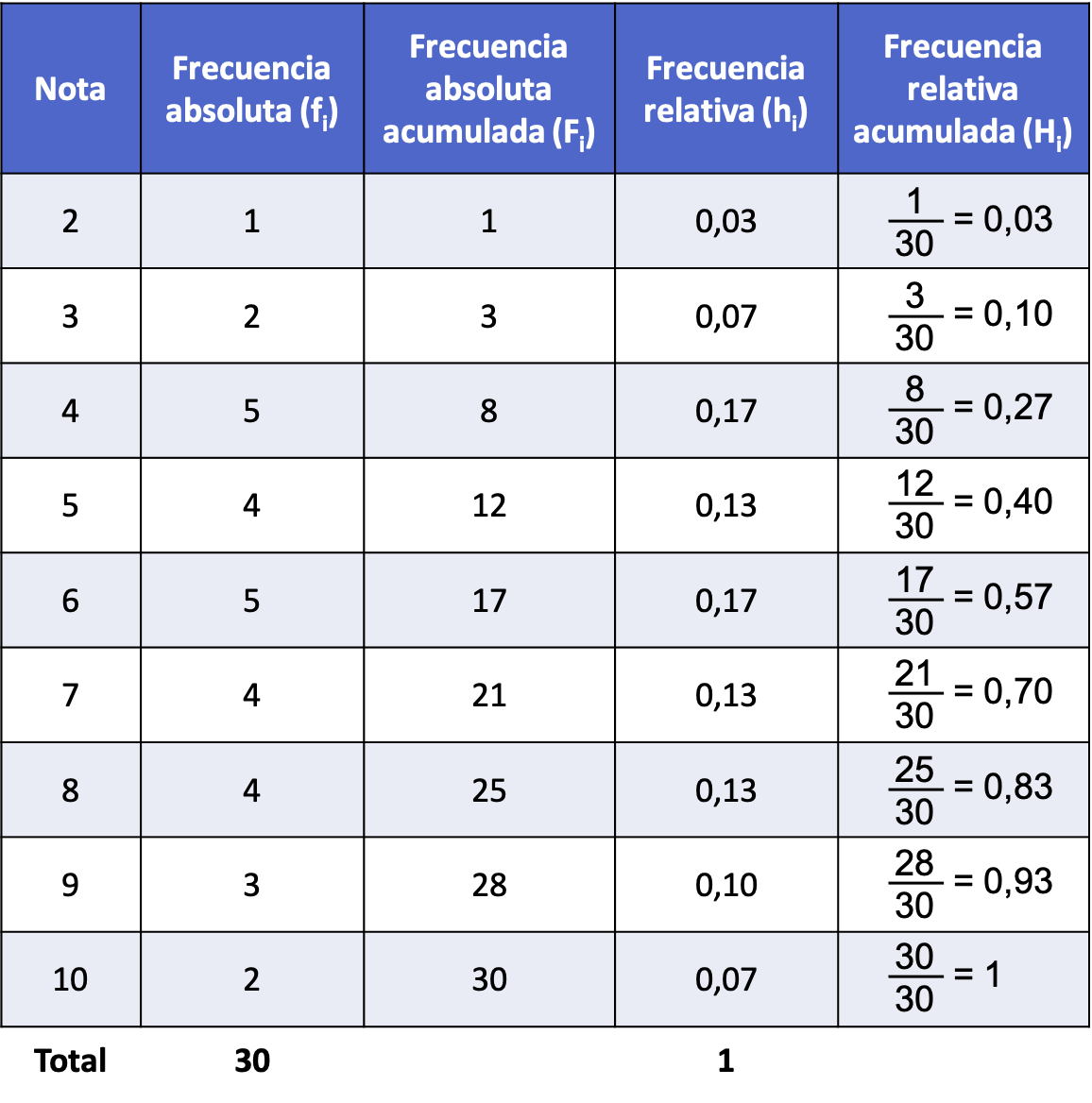
Powyższa tabela, ponieważ zawiera wszystkie rodzaje częstotliwości statystycznych, nazywana jest tabelą częstości. Kliknij tutaj, aby dowiedzieć się więcej: