Co to jest spisek blanda-altmana? (definicja – przykład)

Wykres Blanda-Altmana służy do wizualizacji różnic pomiarowych między dwoma różnymi instrumentami lub dwiema różnymi technikami pomiarowymi.

Często używa się go do oceny podobieństwa nowego instrumentu lub techniki pomiaru czegoś do aktualnie używanego instrumentu lub techniki.

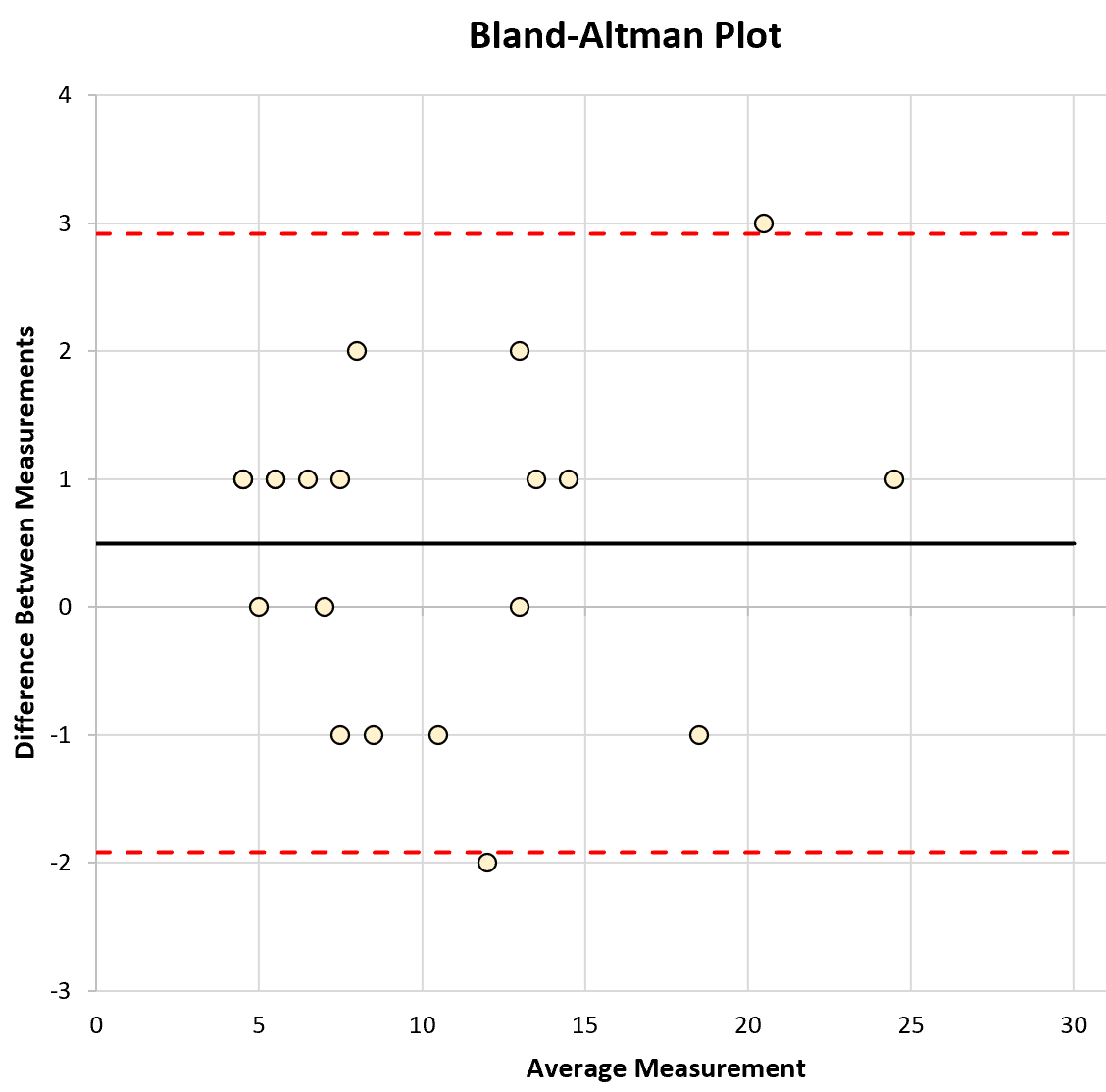
Oś x wykresu przedstawia średni pomiar dokonany przez dwa instrumenty, a oś y przedstawia różnicę w pomiarach pomiędzy dwoma instrumentami.

Na wykresie wyświetlane są również następujące trzy linie:

• Średnia różnica w pomiarach między dwoma instrumentami
• Górna granica 95% przedziału ufności dla średniej różnicy
• Dolna granica 95% przedziału ufności dla średniej różnicy

Ten typ wykresu jest przydatny do określenia dwóch rzeczy:

1. Jaka jest średnia różnica w pomiarach pomiędzy obydwoma instrumentami?

Pozioma linia narysowana pośrodku wykresu pokazuje średnią różnicę pomiarów pomiędzy dwoma instrumentami. Wartość tę często określa się jako „odchylenie” pomiędzy instrumentami.

Im dalej ta wartość jest od zera, tym większa jest średnia różnica w pomiarach pomiędzy instrumentami.

2. Jaki jest typowy zakres zgodności pomiędzy obydwoma instrumentami?

Górne i dolne linie przedziału ufności dają nam wyobrażenie o typowym zakresie zgodności pomiędzy obydwoma instrumentami. Ogólnie rzecz biorąc, 95% różnic między tymi dwoma instrumentami mieści się w tych granicach ufności.

Im szerszy przedział ufności, tym szerszy zakres różnic pomiarowych pomiędzy obydwoma instrumentami.

Poniższy przykład pokazuje krok po kroku, jak od podstaw utworzyć i zinterpretować wykres Blanda-Altmana.

Uwaga: Wykres Blanda-Altmana jest czasami nazywany wykresem średniej różnicy Tukeya. Nazwy te używane są zamiennie.

Krok 1: Zbierz dane

Załóżmy, że biolog chce wiedzieć, jak podobne są dwa różne przyrządy do pomiaru masy żab w gramach. Używa dwóch przyrządów (A i B), aby zważyć ten sam zestaw 20 żab.

Wagę żab zmierzoną każdym przyrządem przedstawiono w poniższej tabeli:

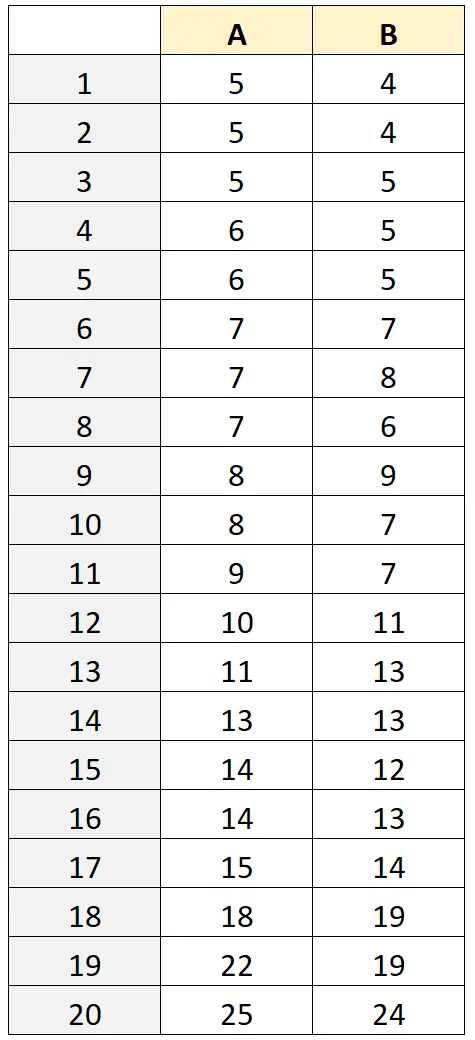
Krok 2: Oblicz średni pomiar i różnicę pomiarów

Następnie obliczymy średni pomiar ((A+B)/2) i różnicę pomiarów (AB) dla każdej żaby:

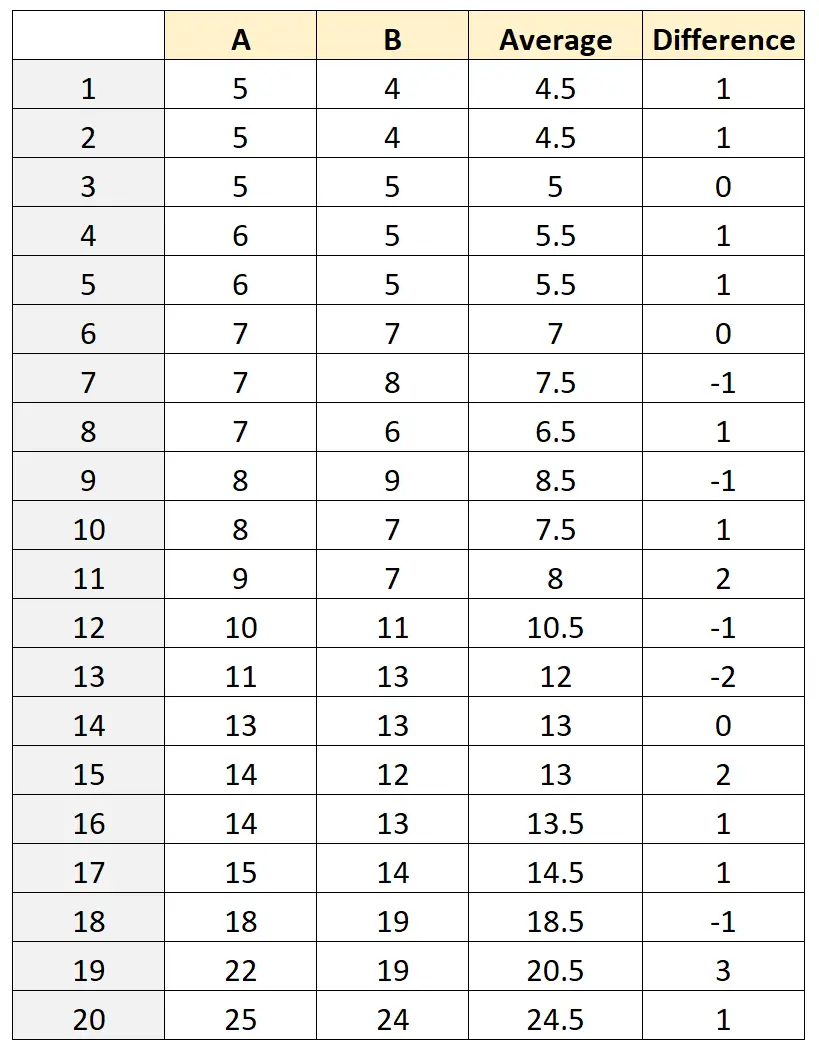
Krok 3: Oblicz średnią różnicę i przedział ufności

Średnia wartości w kolumnie Różnica wynosi 0,5 .

Odchylenie standardowe wartości w kolumnie Różnica wynosi 1,235 .

Górną i dolną granicę przedziału ufności dla średniej różnicy można obliczyć w następujący sposób:

Górna granica: x + 1,96*s = 0,5 + 1,96*1,235 = 2,92

Dolna granica: x – 1,96*s = 0,5 – 1,96*1,235 = -1,92

Oto jak interpretować te wartości:

• Przyrząd A waży średnio o 0,5 grama więcej niż przyrząd B.
• 95% różnic wagowych między obydwoma instrumentami powinno mieścić się w przedziale od -1,92 grama do 2,92 grama.

Następnie utworzymy wykres Blanda-Altmana, aby zwizualizować te wartości.

Krok 4: Utwórz fabułę

Następnie możemy utworzyć następujący wykres przedstawiający średni pomiar dwóch instrumentów na osi x i różnicę między pomiarami na osi y.

Możemy również dodać poziomą linię do średniej różnicy między pomiarami (0,5) oraz górnej granicy ufności (2,92) i dolnej granicy ufności (-1,92), które obliczyliśmy w poprzednim kroku:

Dodatkowe zasoby

Jak utworzyć wykres Blanda-Altmana w programie Excel
Jak utworzyć wykres Blanda-Altmana w R
Jak utworzyć fabułę Blanda-Altmana w Pythonie