Jak używać solidnych błędów standardowych w regresji w stata

Wielokrotna regresja liniowa to metoda, którą możemy wykorzystać do zrozumienia związku między wieloma zmiennymi objaśniającymi a zmienną odpowiedzi.

Niestety, problem często występujący podczas regresji nazywany jest heteroskedastycznością , w której występuje systematyczna zmiana wariancji reszt w pewnym zakresie mierzonych wartości.

Prowadzi to do wzrostu wariancji oszacowań współczynników regresji, ale model regresji nie uwzględnia tego. To sprawia, że znacznie bardziej prawdopodobne jest, że model regresji będzie twierdził, że składnik modelu jest istotny statystycznie, podczas gdy w rzeczywistości tak nie jest.

Jednym ze sposobów wyjaśnienia tego problemu jest użycie solidnych błędów standardowych , które są bardziej „odporne” na problem heteroskedastyczności i zwykle zapewniają dokładniejszą miarę prawdziwego błędu standardowego współczynnika regresji.

W tym samouczku wyjaśniono, jak używać solidnych błędów standardowych w analizie regresji w Stata.

Przykład: Solidne błędy standardowe w Stata

Wykorzystamy automatycznie zintegrowany zbiór danych Stata, aby zilustrować, jak używać solidnych błędów standardowych w regresji.

Krok 1: Załaduj i wyświetl dane.

Najpierw użyj następującego polecenia, aby załadować dane:

automatyczne korzystanie z systemu

Następnie wyświetl surowe dane za pomocą następującego polecenia:

br

Krok 2: Wykonaj wielokrotną regresję liniową bez solidnych błędów standardowych.

Następnie wprowadzimy następujące polecenie, aby wykonać wielokrotną regresję liniową, używając ceny jako zmiennej odpowiedzi oraz mpg i wagi jako zmiennych objaśniających:

regresja cena mpg waga

Krok 3: Wykonaj wielokrotną regresję liniową, korzystając z solidnych błędów standardowych.

Teraz wykonamy dokładnie tę samą wielokrotną regresję liniową, ale tym razem użyjemy polecenia vce(robust) , aby Stata wiedział, jak używać solidnych błędów standardowych:

regresja cena mpg waga, vce (solidny)

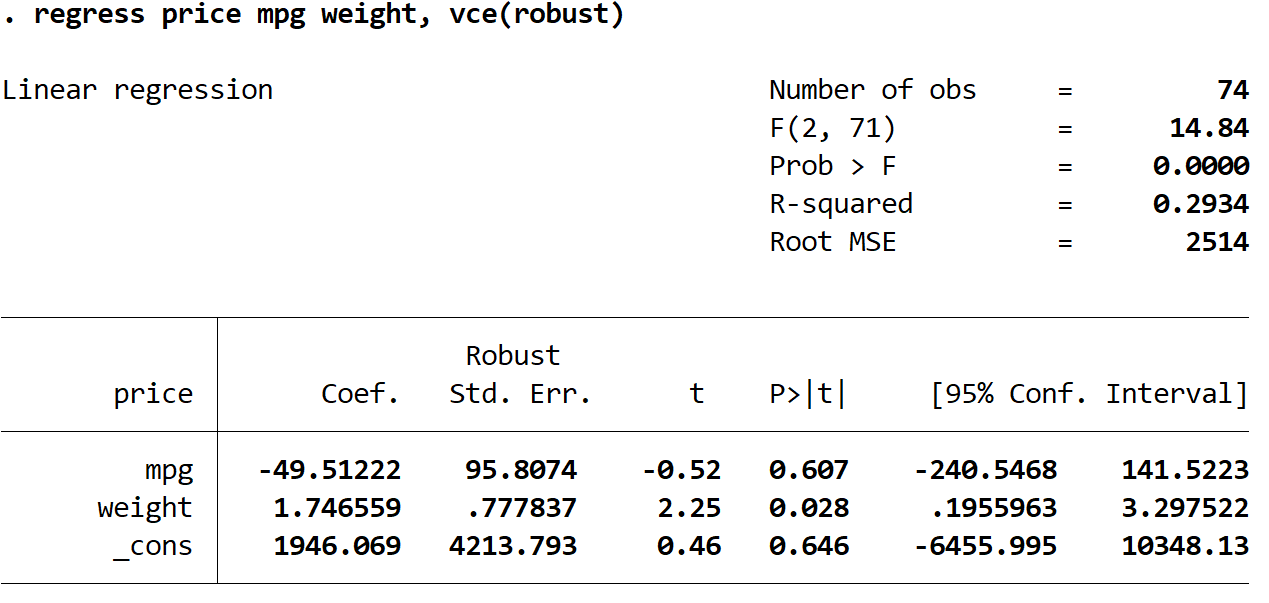
Warto tutaj zwrócić uwagę na kilka ciekawych rzeczy:

1. Oszacowania współczynników pozostały takie same . Kiedy używamy solidnych błędów standardowych, szacunki współczynników w ogóle się nie zmieniają. Należy zauważyć, że szacunki współczynników dla mpg, masy i stałej są następujące dla obu regresji:

• mpg: -49,51222
• waga: 1,746559
• _przeciw: 1946.069

2. Zmieniły się błędy standardowe . Należy zauważyć, że gdy zastosowaliśmy solidne błędy standardowe, błędy standardowe dla każdego oszacowania współczynników wzrosły.

Uwaga: W większości przypadków odporne błędy standardowe będą większe niż normalne błędy standardowe, ale w rzadkich przypadkach możliwe jest, że odporne błędy standardowe będą w rzeczywistości mniejsze.

3. Statystyka testowa każdego współczynnika uległa zmianie. Należy zauważyć, że wartość bezwzględna każdej statystyki testowej t spadła. W efekcie statystykę testową oblicza się jako oszacowany współczynnik podzielony przez błąd standardowy. Zatem im większy błąd standardowy, tym mniejsza wartość bezwzględna statystyki testowej.

4. Wartości p uległy zmianie . Należy zauważyć, że wartości p dla każdej zmiennej również wzrosły. Dzieje się tak, ponieważ mniejsze statystyki testowe są powiązane z większymi wartościami p.

Chociaż wartości p dla naszych współczynników uległy zmianie, zmienna mpg nadal nie jest istotna statystycznie przy α = 0,05, a zmienna waga jest nadal istotna statystycznie przy α = 0,05.