Jak wykonać test t dla par próbek w programie excel

Test t dla par prób służy do porównania średnich z dwóch próbek, gdy każdą obserwację w jednej próbie można powiązać z obserwacją w drugiej próbie.

W tym samouczku wyjaśniono, jak wykonać test t dla par próbek w programie Excel.

Jak wykonać test t dla par próbek w programie Excel

Załóżmy, że chcemy wiedzieć, czy określony program nauczania ma znaczący wpływ na wyniki uczniów na konkretnym egzaminie. Aby to sprawdzić, prosimy 20 uczniów w klasie o przystąpienie do testu wstępnego. Następnie każdy z uczniów uczestniczy w programie nauczania przez dwa tygodnie. Następnie uczniowie ponownie przystępują do testu o podobnym stopniu trudności.

Aby porównać różnicę między średnimi wynikami pierwszego i drugiego testu, używamy testu t dla par prób, ponieważ w przypadku każdego ucznia jego wynik w pierwszym teście można powiązać z wynikiem w drugim teście.

Poniższy obraz przedstawia wyniki każdego ucznia przed testem i po teście:

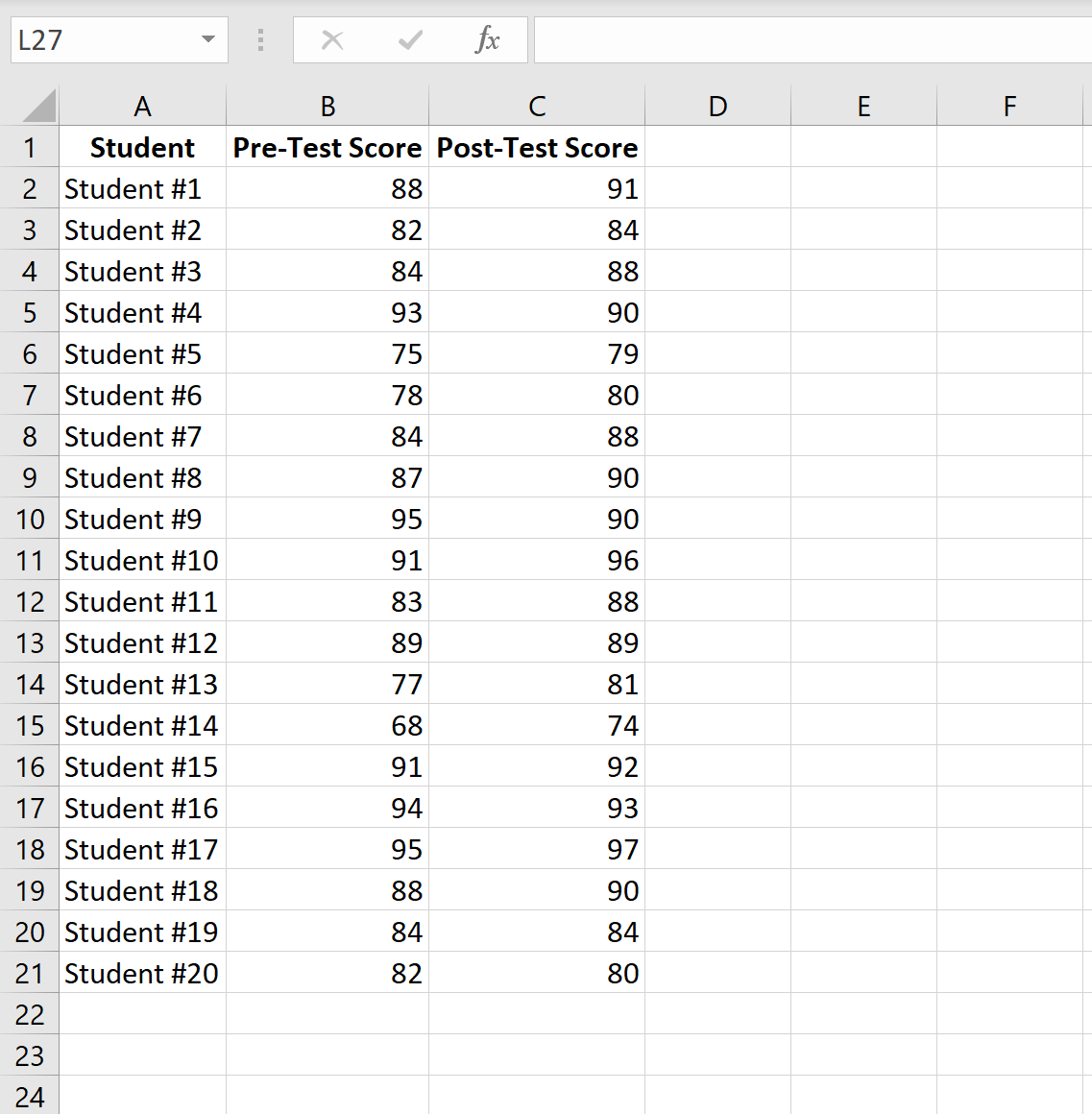
Wykonaj poniższe kroki, aby przeprowadzić test t dla par próbek w celu ustalenia, czy istnieje znacząca różnica w średnich wynikach testu pomiędzy testem przed i po teście.

Krok 1: Otwórz pakiet narzędzi do analizy danych.

Na karcie Dane na górnej wstążce kliknij „Analiza danych”.

Jeśli nie widzisz tej opcji kliknięcia, musisz najpierw pobrać pakiet narzędzi analitycznych , który jest całkowicie bezpłatny.

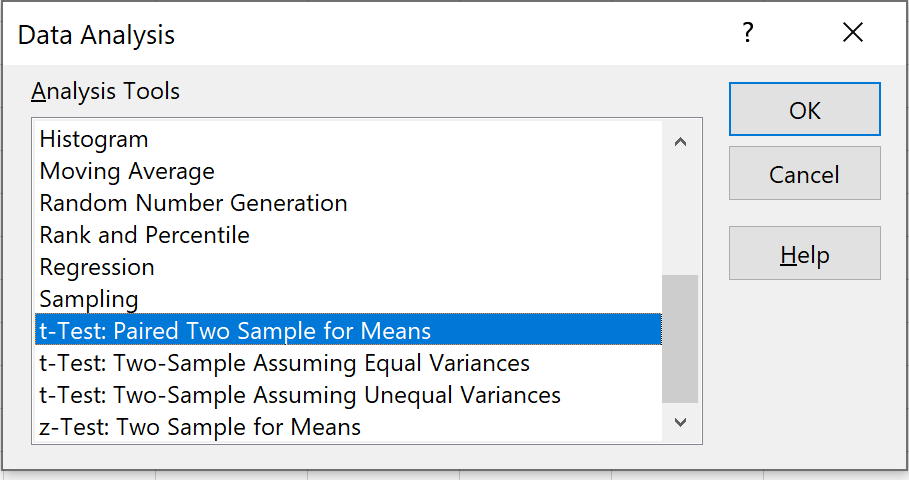
Krok 2: Wybierz odpowiedni test do użycia.

Wybierz opcję z napisem T-Test: Sparowane dwie próbki pod kątem średnich , a następnie kliknij OK.

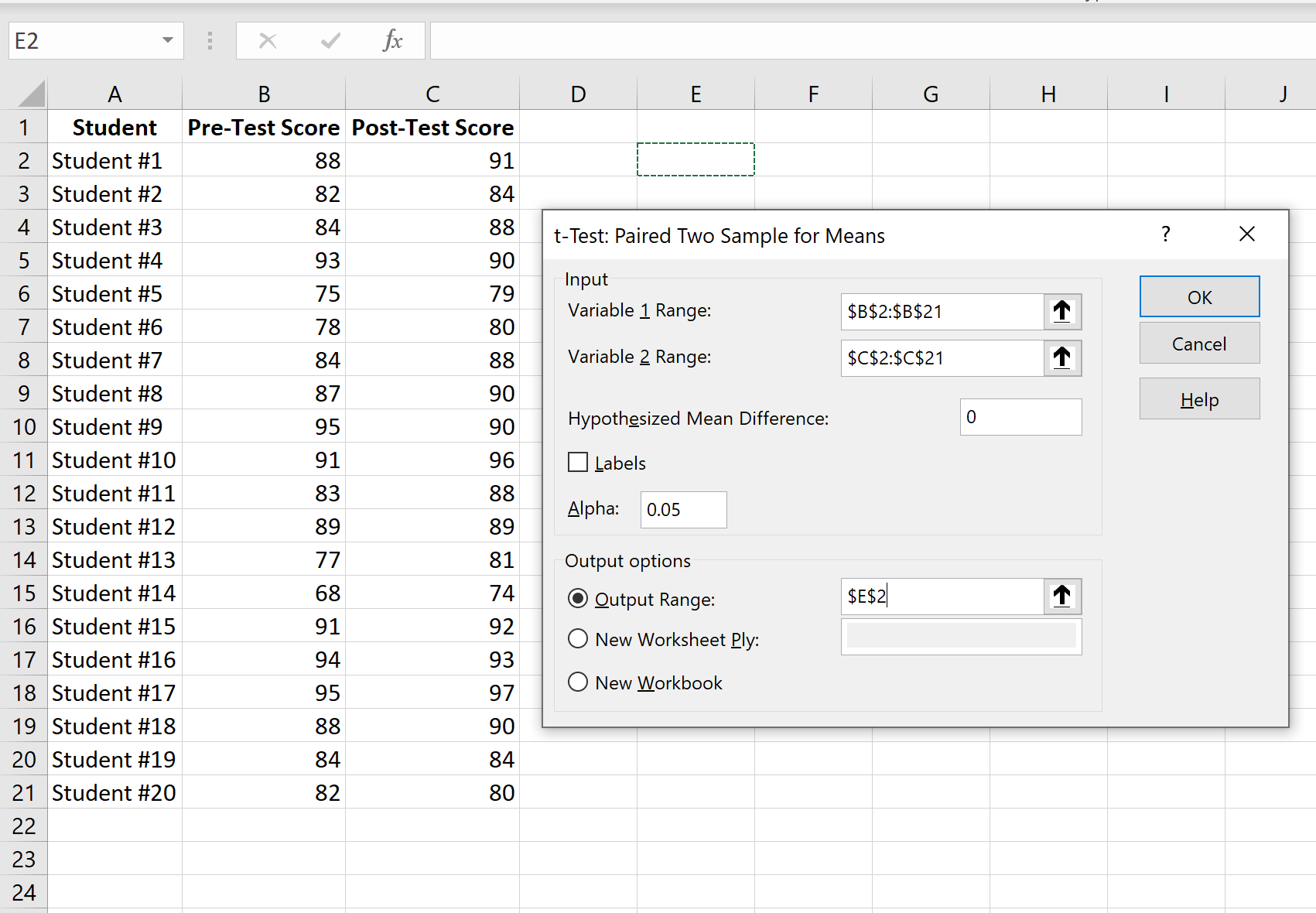
Krok 3: Wprowadź niezbędne informacje.

Wprowadź zakres wartości zmiennej 1 (wyniki przed testem), zmiennej 2 (wyniki po teście), hipotetyczną średnią różnicę (w tym przypadku wpisujemy „0”, ponieważ chcemy wiedzieć, czy prawdziwa różnica średnia między wynikami przed i po teście wynosi 0) oraz zakres wyjściowy, w jakim chcielibyśmy zobaczyć wyświetlane wyniki testu. Następnie kliknij OK.

Krok 4: Interpretacja wyników.

Po kliknięciu przycisku OK w poprzednim kroku zostaną wyświetlone wyniki testu t.

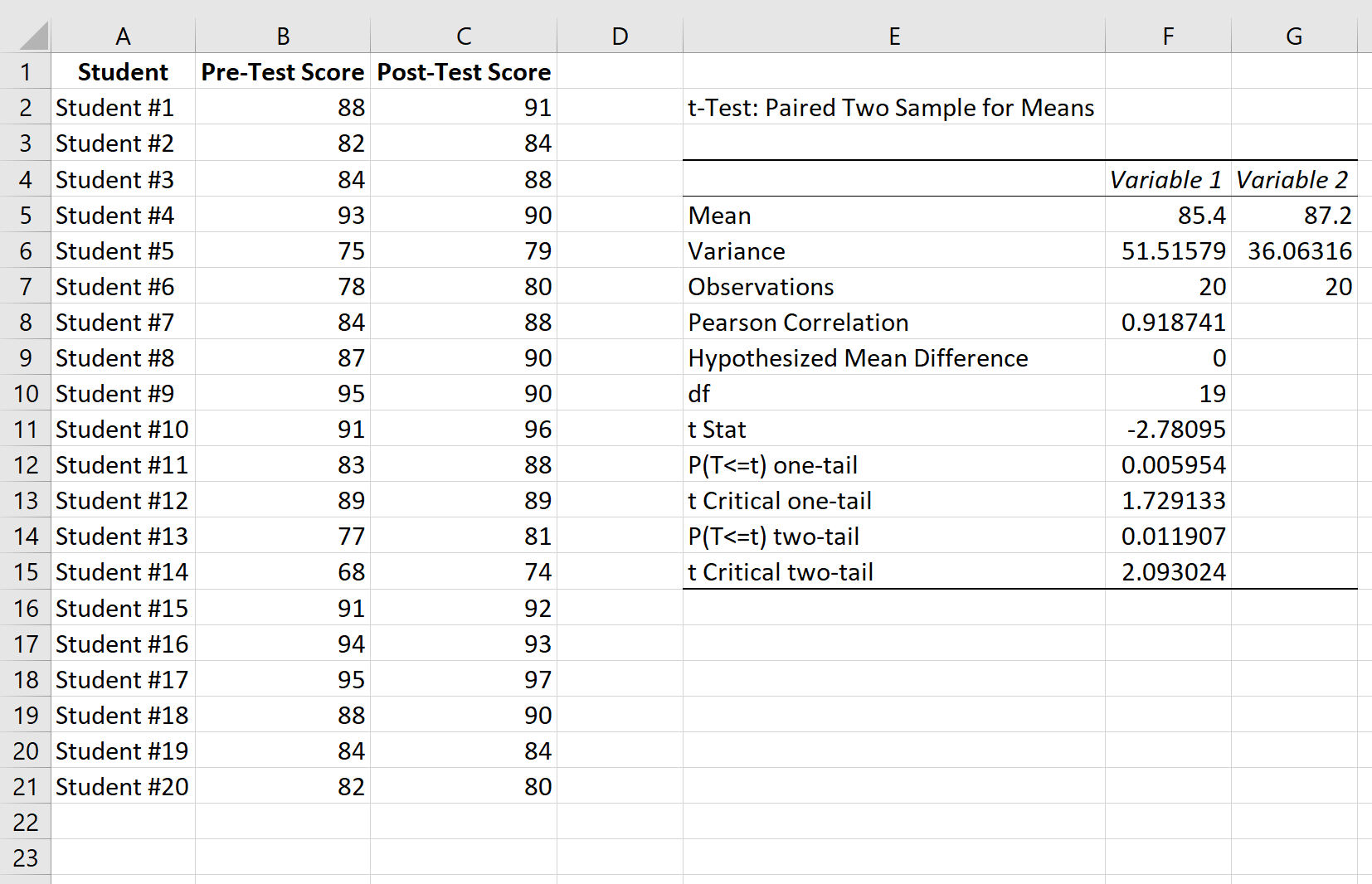
Oto jak interpretować wyniki:

Średnia: Jest to średnia z każdej próbki. Średni wynik przed testem wynosi 85,4 , a średni wynik po teście to 87,2 .

Wariancja: Jest to wariancja dla każdej próbki. Wariancja wyników przed testem wynosi 51,51 , a wariancja wyników po teście wynosi 36,06 .

Obserwacje: Jest to liczba obserwacji w każdej próbce. Obie próbki zawierają 20 obserwacji.

Korelacja Pearsona: Korelacja między wynikami przed testem i wynikami po teście. Okazuje się, że wynosi 0,918 .

Hipotetyczna średnia różnica: Liczba, na temat której „stawiamy hipotezę”, jest różnicą między tymi dwoma średnimi. W tym przypadku wybraliśmy 0 , ponieważ chcemy sprawdzić, czy istnieje różnica między wynikami przed i po teście.

df: Stopnie swobody testu t. Oblicza się to jako n-1, gdzie n to liczba par. W tym przypadku df = 20 – 1 = 19 .

t Stat: Statystyka testu t , która wynosi -2,78 .

Dwustronny P(T<=t): wartość p dla dwustronnego testu t. W tym przypadku p = 0,011907 . Jest to mniej niż alfa = 0,05, więc odrzucamy hipotezę zerową. Mamy wystarczające dowody, aby stwierdzić, że istnieje statystycznie istotna różnica pomiędzy średnim wynikiem przed i po teście.

t Dwustronny krytyczny: Jest to wartość krytyczna testu, określona poprzez identyfikację wartości w tabeli rozkładu t , która odpowiada dwustronnemu testowi z alfa = 0,05 i df = 19. Okazuje się, że wynosi 2, 093024 . Ponieważ wartość bezwzględna naszej statystyki testu t jest większa niż ta wartość, odrzucamy hipotezę zerową. Mamy wystarczające dowody, aby stwierdzić, że istnieje statystycznie istotna różnica pomiędzy średnim wynikiem przed i po teście.

Należy zauważyć, że podejście oparte na wartości p i wartości krytycznej doprowadzi do tego samego wniosku.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne testy t w programie Excel:

Jak wykonać test t dla jednej próby w programie Excel
Jak wykonać test t dla dwóch próbek w programie Excel