Jak wykonać test t dla sparowanych próbek w spss
Test t dla par prób służy do porównania średnich z dwóch próbek, gdy każdą obserwację w jednej próbie można powiązać z obserwacją w drugiej próbie.
W tym samouczku wyjaśniono, jak przeprowadzić test t dla sparowanych próbek w SPSS.
Przykład: Test t dla par próbek w SPSS
Naukowcy chcą wiedzieć, czy nowy sposób uzdatniania paliwa powoduje zmianę średniego zużycia paliwa przez określony samochód. Aby to sprawdzić, przeprowadzają eksperyment, w którym mierzą mpg 12 samochodów z uzdatnieniem paliwa i bez niego.
Ponieważ każdy samochód jest poddawany zabiegowi, możemy przeprowadzić test t dla par, w którym każdy samochód jest ze sobą sparowany, aby określić, czy istnieje różnica w średnim mpg z uzdatnieniem paliwa i bez niego, stosując następujące hipotezy zerowe i alternatywne:
- H 0 : μ 1 = μ 2 (średnie mpg w obu populacjach jest równe)
- H 1 : μ 1 ≠ μ 2 (średnie mpg w obu populacjach nie jest równe)
Poniższy zrzut ekranu pokazuje mpg dla każdego samochodu z (mpg1) i bez (mpg2) uzdatnianiem paliwa:
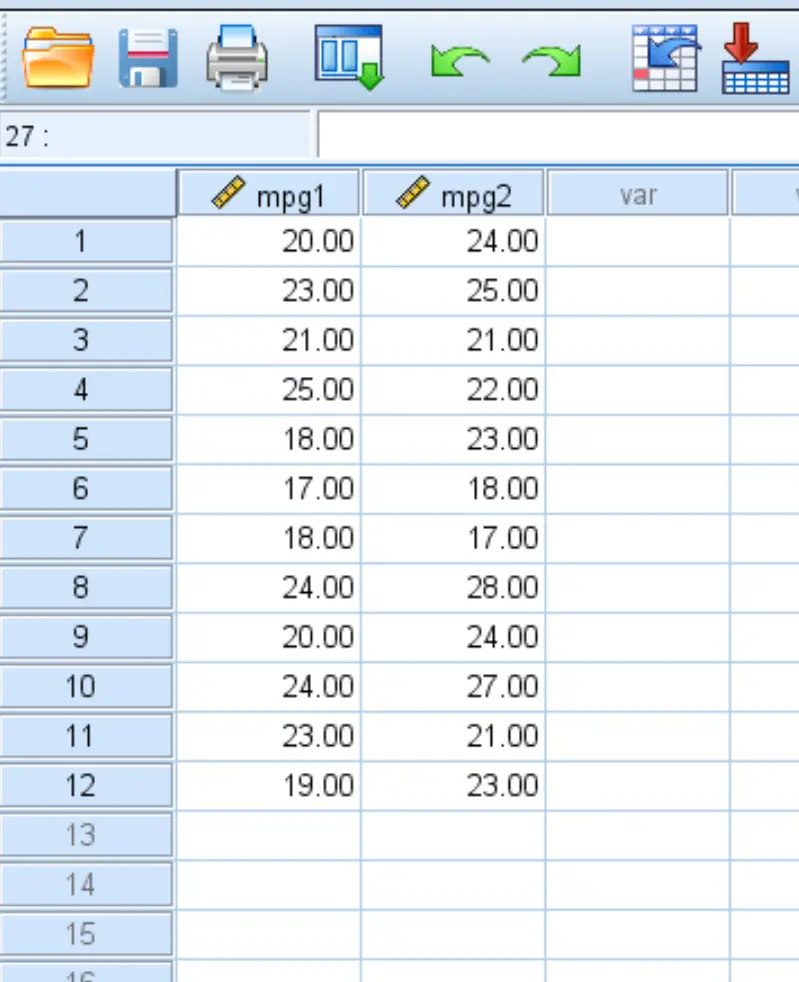
Wykonaj następujące kroki, aby wykonać test t dla par:
Krok 1: Wybierz opcję Test T dla par próbek.
Kliknij kartę Analiza , następnie Porównaj średnie , a następnie Test T dla par próbek :
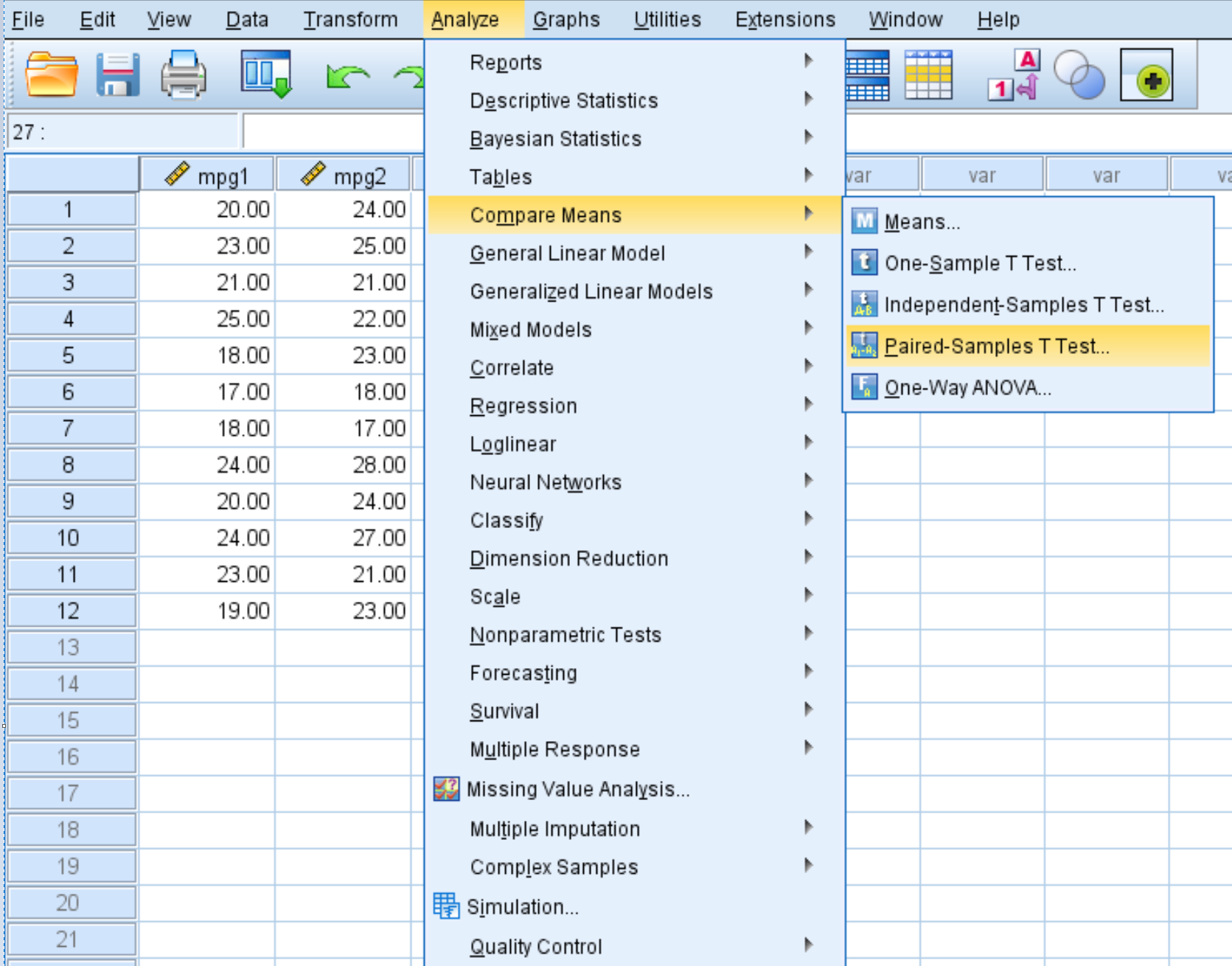
Krok 2: Wpisz niezbędne wartości, aby przeprowadzić test.
Przeciągnij mpg1 do pola pod Zmienną1 i przeciągnij mpg2 do pola pod Zmienną2. Następnie kliknij OK .
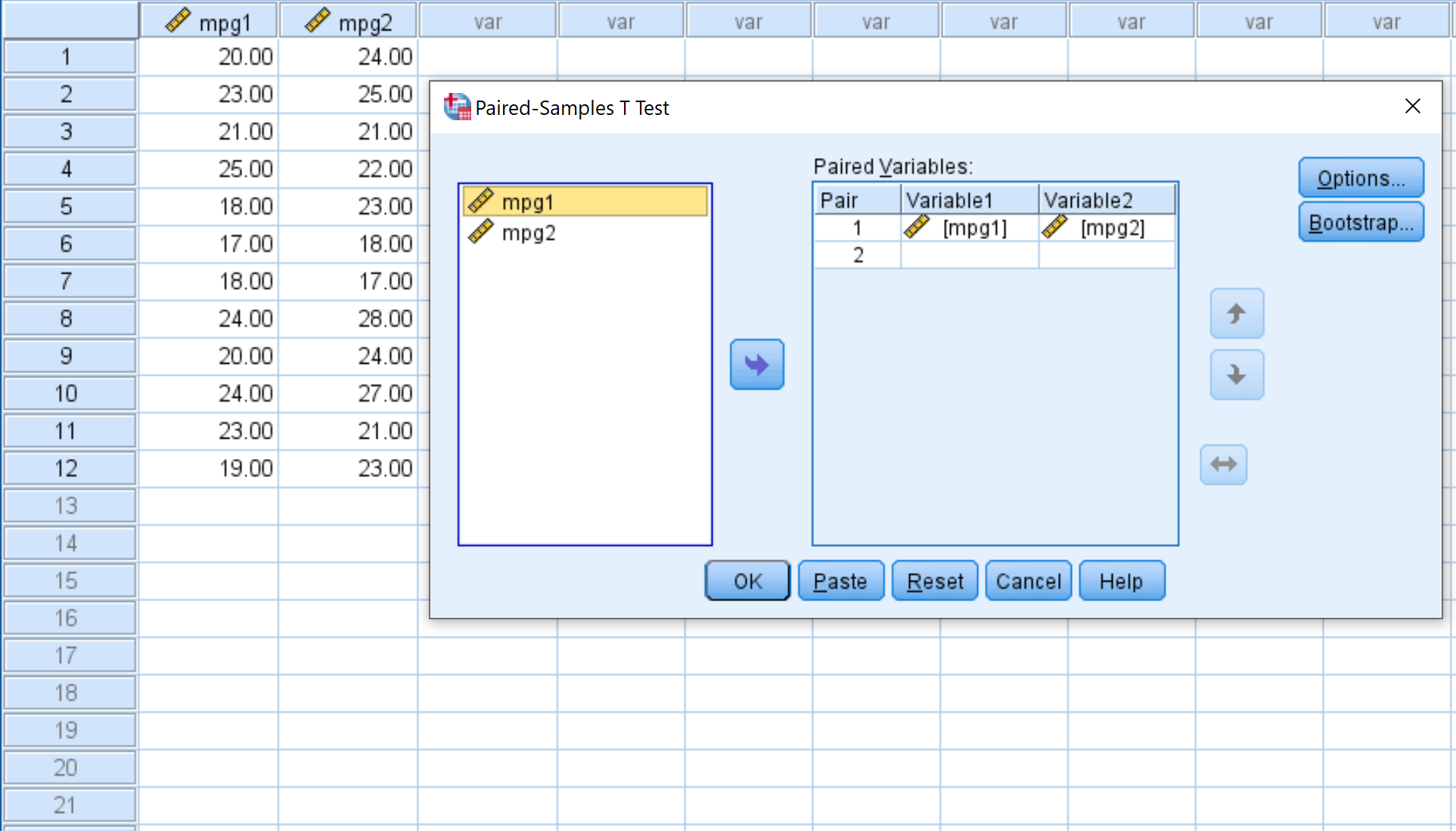
Krok 3: Interpretacja wyników.
Po kliknięciu OK zostaną wyświetlone wyniki testu t dla sparowanych próbek:

Pierwsza tabela przedstawia następujące statystyki podsumowujące dla obu grup:
- N: Wielkość próby w każdej grupie
- Średnia: średnia mpg samochodów w każdej grupie
- Standard. Odchylenie: odchylenie standardowe mpg samochodów w każdej grupie
- Standard. Błąd średni: błąd standardowy średniej wartości mpg, obliczony w s/√n
Ostatnia tabela przedstawia wyniki testu t dla par próbek:
- t: Statystyka testowa, która wynosi -2,244
- df: Stopnie swobody obliczane jako #evens-1 = 12-1 = 11
- Syg. (dwustronny): Dwustronna wartość p, która odpowiada wartości -2,244 przy df=11
Ponieważ wartość p testu (0,046) jest mniejsza niż 0,05, odrzucamy hipotezę zerową. Mamy wystarczająco dużo dowodów, aby stwierdzić, że rzeczywista średnia wartość mpg różni się w przypadku samochodów poddawanych leczeniu i samochodów, które tego nie robią.
Krok 4: Ogłoś wyniki.
Na koniec podamy wyniki naszego testu t dla sparowanych próbek. Oto przykład, jak to zrobić:
Przeprowadzono test t dla 12 samochodów w celu ustalenia, czy nowe uzdatnienie paliwa spowodowało różnicę w średnim przebiegu na galonie.
Wyniki pokazały, że średnia mpg różniła się statystycznie pomiędzy obiema grupami (t = -2,244 przy df=11, p = 0,046) na poziomie istotności 0,05.
95% przedział ufności dla prawdziwej różnicy między średnimi z populacji dał przedział (-3,466; -0,034).