Jak wykonać wielokrotną regresję liniową w spss
Wielokrotna regresja liniowa to metoda, którą możemy wykorzystać do zrozumienia związku między dwiema lub większą liczbą zmiennych objaśniających a zmienną odpowiedzi.
W tym samouczku wyjaśniono, jak przeprowadzić wielokrotną regresję liniową w SPSS.
Przykład: wielokrotna regresja liniowa w SPSS
Załóżmy, że chcemy wiedzieć, czy liczba godzin spędzonych na nauce i liczba zdanych egzaminów próbnych wpływają na ocenę, jaką student otrzymuje z danego egzaminu. Aby to zbadać, możemy przeprowadzić wielokrotną regresję liniową, korzystając z następujących zmiennych:
Wyjaśniające zmienne:
- Godziny nauki
- Egzaminy przygotowawcze zaliczone
Zmienna odpowiedzi:
- Wynik egazminu
Wykonaj poniższe kroki, aby wykonać tę wielokrotną regresję liniową w SPSS.
Krok 1: Wprowadź dane.
Wprowadź następujące dane dotyczące liczby godzin nauki, zdanych egzaminów przygotowawczych i uzyskanych wyników egzaminów dla 20 uczniów:
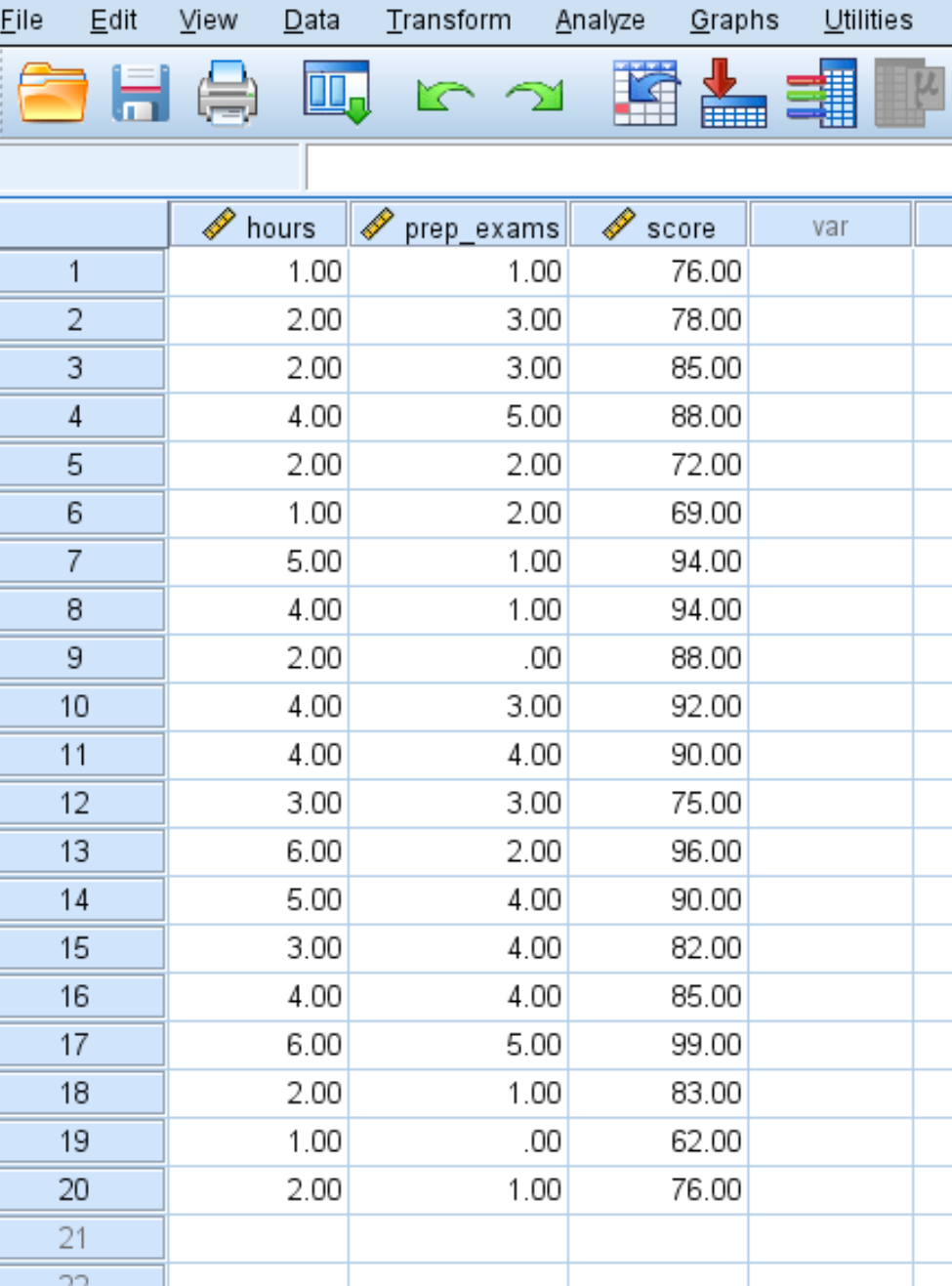
Krok 2: Wykonaj wielokrotną regresję liniową.
Kliknij kartę Analiza , następnie Regresja , a następnie Liniowa :
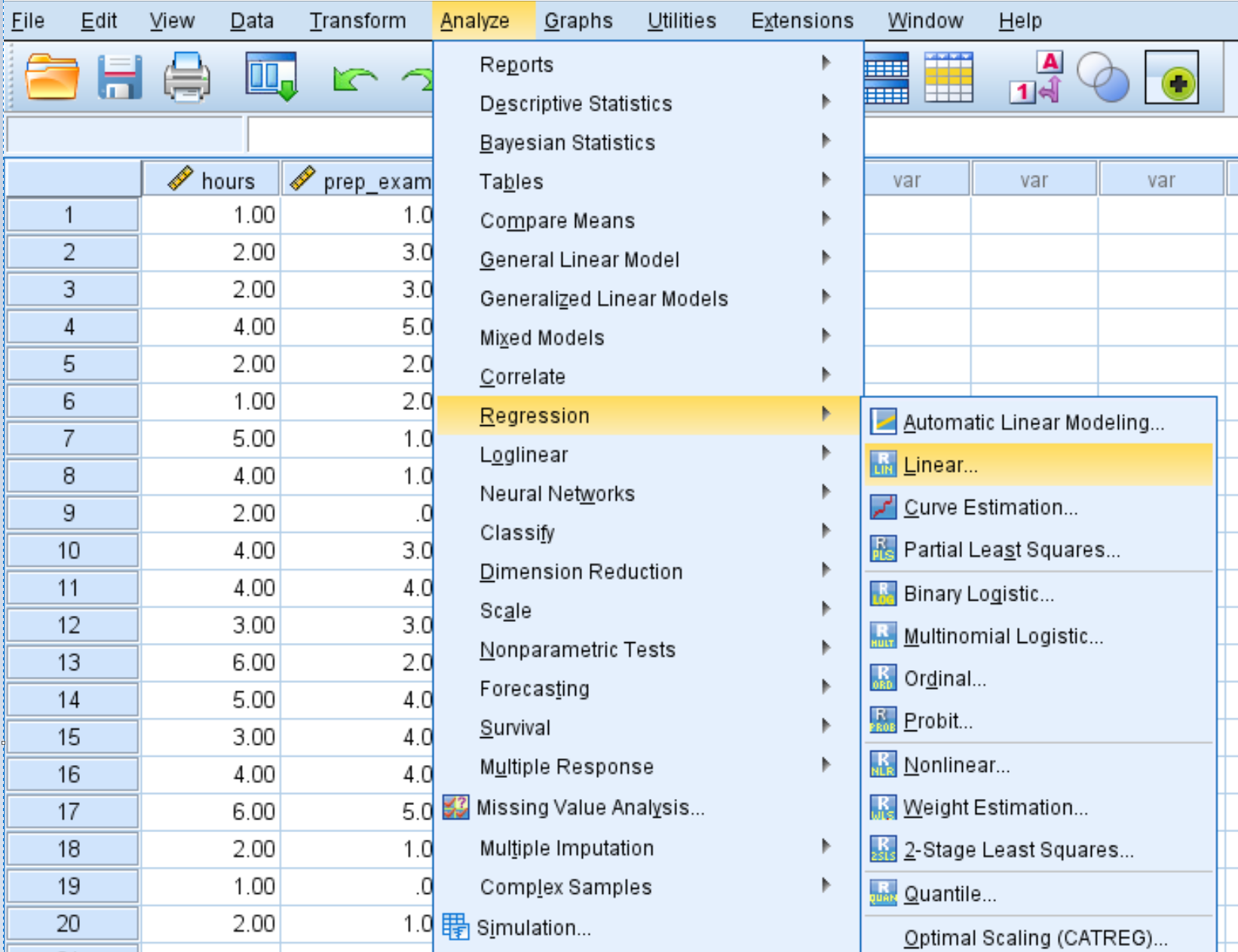
Przeciągnij wynik zmiennej do pola Zależne. Przeciągnij zmienne hours i prep_exams do pola oznaczonego Independent(s). Następnie kliknij OK .
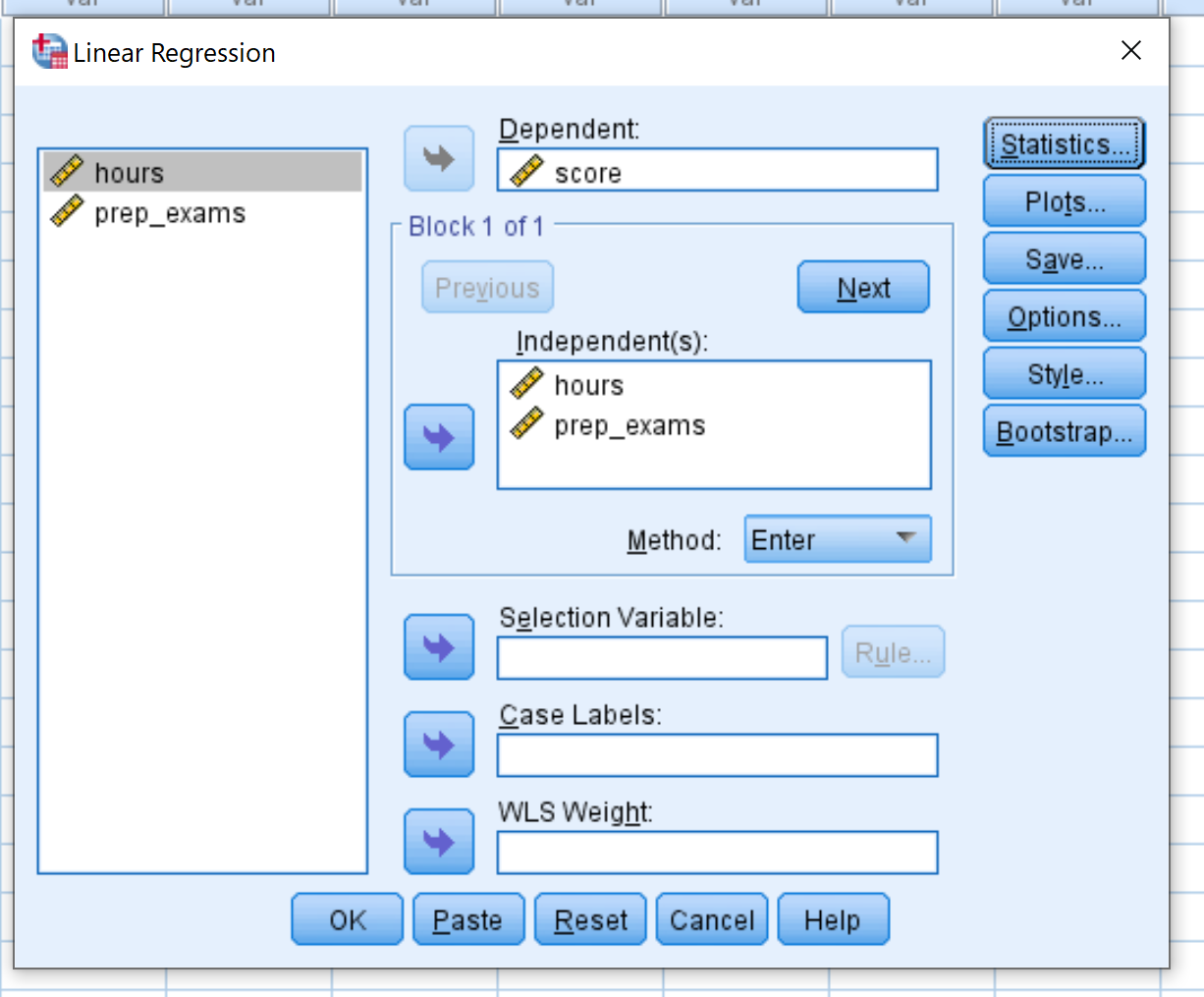
Krok 3: Zinterpretuj wynik.
Po kliknięciu OK wyniki wielokrotnej regresji liniowej pojawią się w nowym oknie.
Pierwsza tabela, która nas interesuje, nazywa się Podsumowaniem modelu :
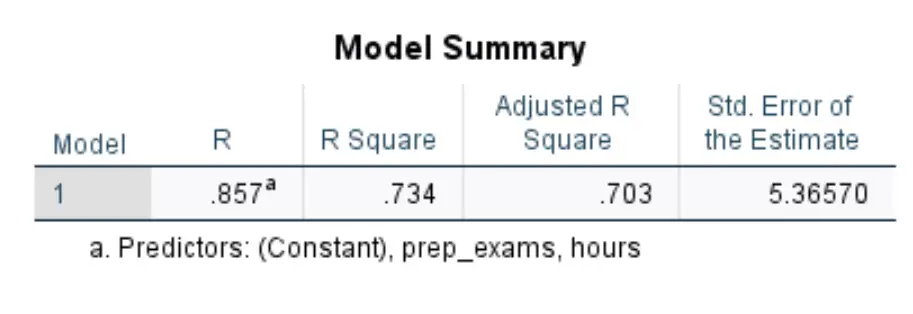
Oto jak interpretować najbardziej odpowiednie liczby w tej tabeli:
- Kwadrat R: Jest to proporcja wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennych objaśniających. W tym przykładzie 73,4% różnic w wynikach egzaminów można wyjaśnić liczbą przepracowanych godzin i liczbą zdanych egzaminów przygotowawczych.
- Standard. Błąd estymacji: błąd standardowy to średnia odległość pomiędzy obserwowanymi wartościami a linią regresji. W tym przykładzie zaobserwowane wartości odbiegają średnio o 5,3657 jednostki od linii regresji.
Następna tabela, która nas interesuje, nazywa się ANOVA :
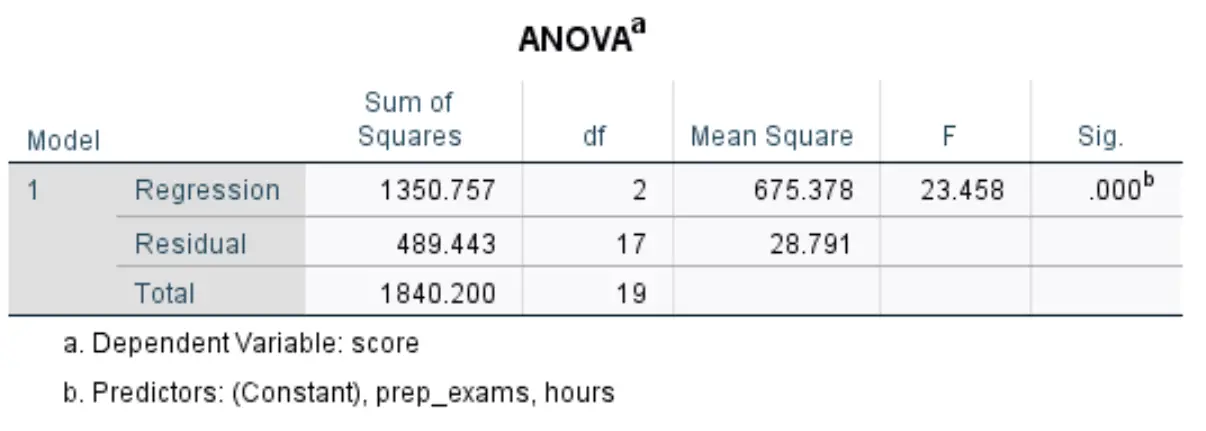
Oto jak interpretować najbardziej odpowiednie liczby w tej tabeli:
- F: Jest to ogólna statystyka F dla modelu regresji, obliczona jako regresja średniokwadratowa / reszta średniokwadratowa.
- Sig: Jest to wartość p powiązana z ogólną statystyką F. To mówi nam, czy model regresji jako całość jest statystycznie istotny, czy nie. Innymi słowy, mówi nam, czy dwie zmienne objaśniające łącznie mają statystycznie istotny związek ze zmienną odpowiedzi. W tym przypadku wartość p wynosi 0,000, co wskazuje, że zmienne objaśniające, przepracowane godziny i zdane egzaminy przygotowawcze mają istotny statystycznie związek z wynikiem egzaminu.
Poniższa tabela, która nas interesuje, nosi tytuł Współczynniki :
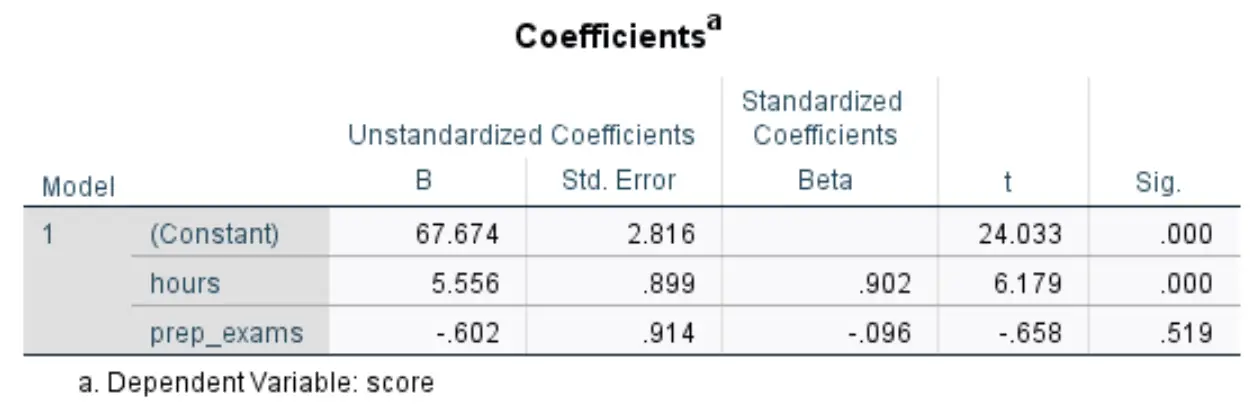
Oto jak interpretować najbardziej odpowiednie liczby w tej tabeli:
- B niestandaryzowany (stała): mówi nam o średniej wartości zmiennej odpowiedzi, gdy obie zmienne predykcyjne wynoszą zero. W tym przykładzie średni wynik egzaminu wynosi 67 674 , podczas gdy liczba godzin nauki i zdanych egzaminów przygotowawczych wynosi zero.
- Niestandaryzowane B (godziny): Informuje nas o średniej zmianie wyników egzaminów związanej ze wzrostem liczby godzin nauki o jedną jednostkę, przy założeniu, że liczba zdanych egzaminów przygotowawczych pozostaje stała. W tym przypadku każda dodatkowa godzina spędzona na nauce wiąże się ze wzrostem punktacji z egzaminu o 5556 punktów, przy założeniu stałej liczby zdawanych egzaminów praktycznych.
- Niestandaryzowane B (prep_exams): Informuje nas o średniej zmianie wyniku egzaminu związanej ze wzrostem o jedną jednostkę liczby zdanych egzaminów przygotowawczych, przy założeniu, że liczba godzin nauki pozostaje stała. W takim przypadku każdy dodatkowy zdany egzamin przygotowawczy wiąże się z obniżeniem oceny z egzaminu o 0,602 punktu, przy założeniu stałej liczby godzin nauki.
- Syg. (godziny): Jest to wartość p zmiennej objaśniającej godziny . Ponieważ ta wartość (0,000) jest mniejsza niż 0,05, możemy stwierdzić, że przestudiowane godziny mają statystycznie istotny związek z wynikami egzaminów.
- Syg. (prep_exams): Jest to wartość p zmiennej objaśniającej prep_exams . Ponieważ wartość ta (0,519) jest nie mniejsza niż 0,05, nie można stwierdzić, że liczba zdanych egzaminów przygotowawczych ma istotny statystycznie związek z wynikiem egzaminu.
Na koniec możemy utworzyć równanie regresji, korzystając z wartości pokazanych w tabeli dla stałych , godzin i prep_exams . W tym przypadku równanie wyglądałoby następująco:
Szacowany wynik egzaminu = 67,674 + 5,556*(godziny) – 0,602*(prep_exams)
Możemy użyć tego równania, aby znaleźć szacowany wynik egzaminu studenta na podstawie liczby godzin nauki i liczby egzaminów praktycznych, które zdawał. Przykładowo student, który uczy się 3 godziny i podchodzi do 2 egzaminów przygotowawczych, powinien otrzymać ocenę 83,1:
Szacowany wynik egzaminu = 67,674 + 5,556*(3) – 0,602*(2) = 83,1
Uwaga: Ponieważ zmienna objaśniająca dla egzaminów przygotowawczych nie okazała się istotna statystycznie, możemy zdecydować się na usunięcie jej z modelu i zamiast tego przeprowadzić prostą regresję liniową , wykorzystując przestudiowane godziny jako jedyną zmienną objaśniającą.