Środki geometryczne

Przez Benjamin Anderson 6 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniamy, czym jest średnia geometryczna, jak ją oblicza się i jaka jest różnica między średnią geometryczną a średnią arytmetyczną. Będzie można także zobaczyć krok po kroku rozwiązane ćwiczenie średniej geometrycznej oraz jakie są właściwości tego typu średniej. Na koniec znajdziesz kalkulator umożliwiający obliczenie średniej geometrycznej dowolnego zbioru danych.

Co to jest średnia geometryczna?

Średnia geometryczna jest miarą centralności statystyki opisowej. Średnia geometryczna zbioru danych statystycznych jest równa n-temu pierwiastkowi iloczynu wszystkich wartości.

Średnia geometryczna jest wykorzystywana w finansach przedsiębiorstw do obliczania stóp zwrotu, średnich procentowych i odsetek składanych.

Wzór na średnią geometryczną jest zatem następujący:

Średnią geometryczną można obliczyć tylko wtedy, gdy wszystkie dane w próbce są dodatnie. Ponieważ jeśli wartość jest ujemna, pierwiastek miałby rozwiązanie ujemne lub nie miałby żadnego rozwiązania, z drugiej strony, jeśli dana wynosi zero, to mnożenie danych dałoby zero, a zatem średnia geometryczna byłaby równa 0.

Średnia geometryczna nie jest jedynym rodzajem średniej, jaki istnieje. Istnieje również średnia arytmetyczna, średnia ważona, średnia kwadratowa i średnia harmoniczna.

Różnica między średnią geometryczną a średnią arytmetyczną

Główna różnica między średnią geometryczną a średnią arytmetyczną polega na tym, że średnia geometryczna jest mniej wrażliwa na wartości ekstremalne niż średnia arytmetyczna. Dodatkowo średnią arytmetyczną można obliczyć przy wartościach ujemnych i zerowych, natomiast średnią geometryczną można obliczyć tylko przy wartościach dodatnich.

Podobnie średnia geometryczna będzie na ogół niższa niż średnia arytmetyczna dla tego samego zbioru danych.

Należy również zauważyć, że obliczenie średniej geometrycznej jest bardziej złożone i dlatego jej istotność statystyczna jest trudniejsza do interpretacji.

Krótko mówiąc, średnia geometryczna ma zalety i wady w porównaniu ze średnią arytmetyczną i, w zależności od charakteru danych, właściwe będzie obliczenie tej lub innej średniej.

Jak obliczyć średnią geometryczną

Aby obliczyć średnią geometryczną, należy wykonać następujące kroki:

Oblicz iloczyn wszystkich danych statystycznych w próbie.
Znajdź n-ty pierwiastek obliczonego produktu.
Otrzymany wynik jest średnią geometryczną próbki statystycznej.

Jak widać, znalezienie średniej geometrycznej zbioru danych jest stosunkowo proste za pomocą kalkulatora lub programu komputerowego, ponieważ wystarczy obliczyć iloczyn i pierwiastek. Wręcz przeciwnie, ręczne wykonywanie obliczeń jest dość pracochłonne.

👉 Dlatego zalecamy skorzystanie z poniższego kalkulatora do obliczenia średniej geometrycznej zbioru danych.

Przykład średniej geometrycznej

Kiedy już zapoznamy się z teorią dotyczącą średniej geometrycznej, zrobimy przykład, dzięki któremu będziesz mógł dokładnie zobaczyć, jak uzyskać średnią geometryczną.

Znane są wyniki ekonomiczne firmy za ostatnie pięć lat. W pierwszym roku firma osiągnęła rentowność ekonomiczną na poziomie 10%, w drugim roku zysk osiągnął 23%, w trzecim roku zarobione pieniądze wyniosły 16%, w czwartym roku osiągnęła rentowność ekonomiczną na poziomie 7%, a inwestycja w piątym roku oznaczało zwrot w wysokości 20%. Zostaniesz poproszony o obliczenie średniej ze wszystkich wartości procentowych.

Jak widzieliśmy, aby obliczyć średnią procentów, nie należy używać średniej arytmetycznej, ale raczej wykonywać obliczenia na podstawie średniej geometrycznej.

Dlatego stosujemy wzór na średnią geometryczną:

$MG=\sqrt[n]{\prod_{i=1}^Nx_i}=\sqrt[n]{x_1\cdot x_2\cdot \ldots x_n}$

I podstawiamy przykładowe wartości do wzoru i wykonujemy obliczenia:

$MG=\sqrt[5]{1,10\cdot 1,23\cdot 1,16\cdot 1,07\cdot 1,20}=1,15 \ \longrightarrow \ 15 \%$

Zauważ, że mamy pięć punktów danych, więc obliczamy piąty pierwiastek.

Wynik liczbowy średniej geometrycznej wynosi 1,15, co oznacza, że firma odnotowała wzrost gospodarczy średniorocznie na poziomie 15%.

Należy pamiętać, że udało nam się uzyskać średnią geometryczną, ponieważ wszystkie wartości były dodatnie, ale gdyby jakikolwiek procent był ujemny, musielibyśmy umieścić dane we wzorze jako dodatnią część dziesiętną z częścią całkowitą. równy zeru. Na przykład wzrost -30% należy wyrazić we wzorze jako 0,70 (1-0,3=0,7).

Kalkulator średniej geometrycznej

Podłącz dowolną przykładową statystykę do poniższego kalkulatora, aby znaleźć jej średnią geometryczną. Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego. Pamiętaj, że nie możesz określić średniej geometrycznej, jeśli wartość jest ujemna lub zerowa.

Własności średniej geometrycznej

Średnia geometryczna ma następujące cechy:

Jest to rodzaj średniej, który jest bardzo przydatny do znajdowania średniej wartości procentowych lub wskaźników.

Można to obliczyć tylko wtedy, gdy wszystkie dane są dodatnie.

Znaczenie geometryczne średniej geometrycznej dwóch liczb a i b to bok kwadratu o takim samym polu jak prostokąt, którego boki mają wymiary a i b .

$MG(a,b)=\sqrt{a\cdot b}$

Znaczenie geometryczne średniej geometrycznej trzech liczb a , b i c to bok sześcianu, którego objętość jest równa równoległościanowi boków a , b i c .

$MG(a,b,c)=\sqrt[3]{a\cdot b \cdot c}$

Logarytm średniej geometrycznej zbioru danych stanowi średnią arytmetyczną logarytmów tego samego zbioru.

Średnia geometryczna zbioru wartości będzie zawsze mniejsza lub równa średniej arytmetycznej.

$\sqrt[N]{x_1\cdot x_2\ldots x_N}\leq \cfrac{x_1+x_2+\ldots+x_N}{N}$

Ważoną średnią geometryczną oblicza się w taki sam sposób jak średnią geometryczną, ale poprzez dodanie wag do wykładnika każdej pozycji danych w celu zważenia wartości statystycznych.

$\displaystyle \left(\prod_{i=1}^n{x_i}^{\alpha_i}\right)^{\frac{1}{\sum_i{\alpha_i}}}= \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}} \left}}$

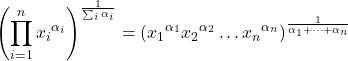
Oblicz średnią geometryczną w programie Excel

Na koniec zobaczmy, jak znaleźć średnią geometryczną zbioru danych za pomocą programu Excel.

Aby obliczyć średnią geometryczną w Excelu, należy skorzystać z funkcji MEANS.GEOM. Po prostu wprowadź wszystkie wartości, dla których chcesz przyjąć średnią geometryczną, a funkcja zwróci wynik średniej geometrycznej.

Na przykład, aby określić średnią geometryczną z powyższego przykładu, należy wpisać w polu Excel =MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) .

Należy pamiętać, że jeśli którakolwiek z wartości będzie równa zero lub ujemna, funkcja zwróci błąd.

Jak widać, obliczenie średniej geometrycznej w programie Excel jest znacznie prostsze i szybsze, ponieważ wystarczy skopiować dane na arkusz i użyć wzoru.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej