Delikatny przewodnik po sumie kwadratów: sst, ssr, sse
Regresja liniowa służy do znalezienia linii, która najlepiej „pasuje” do zbioru danych.
Często używamy trzech różnych sum wartości kwadratów, aby zmierzyć, jak dobrze linia regresji faktycznie pasuje do danych:
1. Suma kwadratów całkowitych (SST) – Suma kwadratów różnic pomiędzy poszczególnymi punktami danych (y i ) a średnią zmiennej odpowiedzi ( y ).
- SST = Σ(y i – y ) 2
2. Regresja sumy kwadratów (SSR) – Suma kwadratów różnic pomiędzy przewidywanymi punktami danych (ŷ i ) a średnią zmiennej odpowiedzi ( y ).
- SSR = Σ(ŷ i – y ) 2
3. Błąd sumy kwadratów (SSE) – Suma kwadratów różnic pomiędzy przewidywanymi punktami danych (ŷ i ) i obserwowanymi punktami danych (y i ).
- SSE = Σ(ŷ i – y i ) 2
Pomiędzy tymi trzema miarami istnieje następująca zależność:
SST = SSR + SSE
Jeśli więc znamy dwa z tych pomiarów, możemy użyć prostej algebry do obliczenia trzeciego.
SSR, SST i kwadrat R
R-kwadrat , czasami nazywany współczynnikiem determinacji, jest miarą tego, jak dobrze model regresji liniowej pasuje do zbioru danych. Reprezentuje proporcję wariancjizmiennej odpowiedzi , którą można wyjaśnić za pomocą zmiennej predykcyjnej.
Wartość R-kwadrat może mieścić się w przedziale od 0 do 1. Wartość 0 oznacza, że zmiennej odpowiedzi nie można w ogóle wyjaśnić za pomocą zmiennej predykcyjnej. Wartość 1 wskazuje, że zmienna odpowiedzi może być doskonale i bezbłędnie wyjaśniona przez zmienną predykcyjną.
Używając SSR i SST, możemy obliczyć R do kwadratu w następujący sposób:
R do kwadratu = SSR / SST
Na przykład, jeśli SSR dla danego modelu regresji wynosi 137,5, a SST wynosi 156, obliczymy R do kwadratu w następujący sposób:
R do kwadratu = 137,5 / 156 = 0,8814
To mówi nam, że 88,14% zmienności zmiennej odpowiedzi można wyjaśnić zmienną predykcyjną.
Oblicz SST, SSR, SSE: przykład krok po kroku
Załóżmy, że mamy następujący zbiór danych, który pokazuje liczbę godzin przestudiowanych przez sześciu różnych uczniów wraz z wynikami ich egzaminów końcowych:
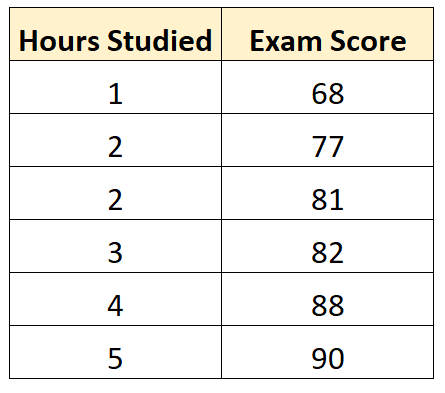
Korzystając z oprogramowania statystycznego (takiego jak R , Excel , Python ) lub nawet ręcznie, możemy zobaczyć, że najlepiej dopasowana linia to:
Wynik = 66,615 + 5,0769*(Godziny)
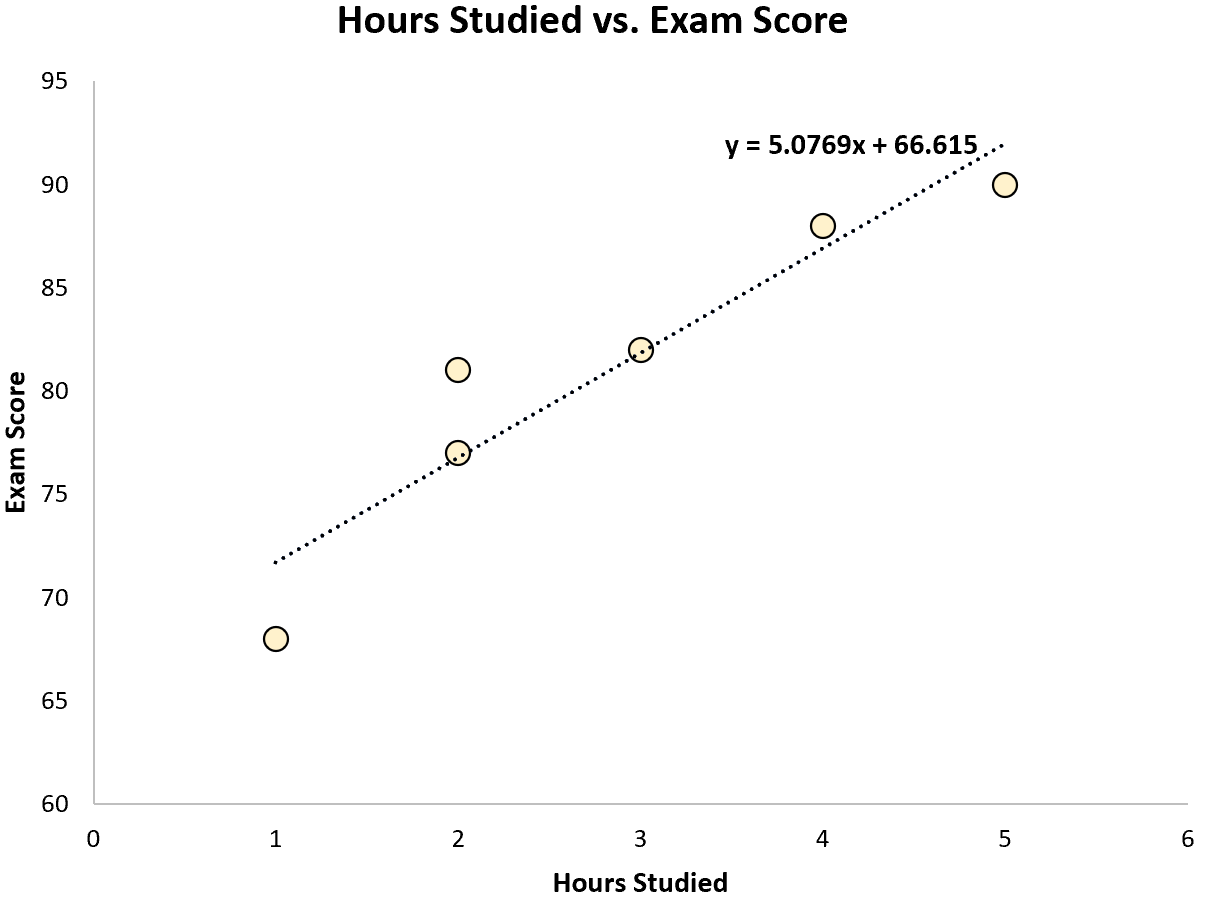
Kiedy już znamy linię równania najlepszego dopasowania, możemy wykonać następujące kroki, aby obliczyć SST, SSR i SSE:
Krok 1: Oblicz średnią zmiennej odpowiedzi.
Okazuje się, że średnia zmiennej odpowiedzi ( y ) wynosi 81 .
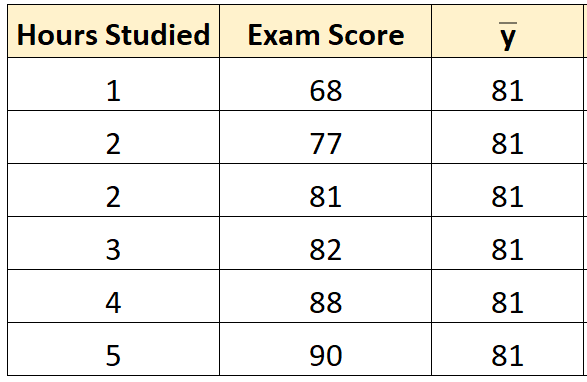
Krok 2: Oblicz przewidywaną wartość dla każdej obserwacji.
Następnie możemy użyć linii równania najlepszego dopasowania, aby obliczyć przewidywany wynik egzaminu () dla każdego ucznia.
Na przykład przewidywana ocena z egzaminu dla ucznia, który uczył się jedną godzinę, to:
Wynik = 66,615 + 5,0769*(1) = 71,69 .
Możemy zastosować to samo podejście, aby znaleźć przewidywany wynik dla każdego ucznia:
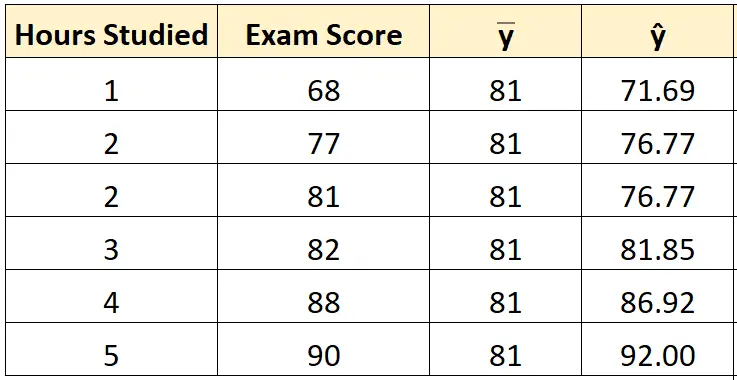
Krok 3: Oblicz całkowitą sumę kwadratów (SST).
Następnie możemy obliczyć całkowitą sumę kwadratów.
Na przykład całkowita suma kwadratów pierwszego ucznia wynosi:
(y ja – y ) 2 = (68 – 81) 2 = 169 .
Możemy zastosować to samo podejście, aby znaleźć całkowitą sumę kwadratów dla każdego ucznia:
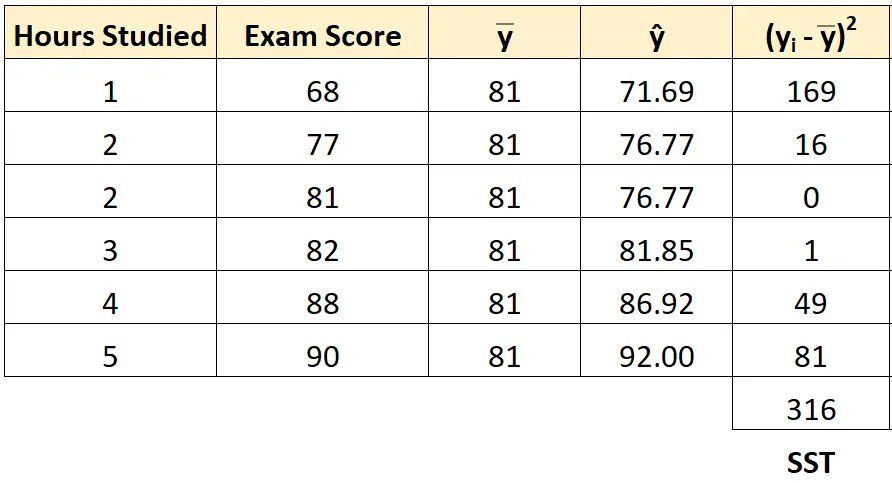
Całkowita suma kwadratów wynosi 316 .
Krok 4: Oblicz sumę kwadratów regresji (SSR).
Następnie możemy obliczyć sumę kwadratów regresji.
Na przykład suma kwadratów regresji dla pierwszego ucznia wynosi:
( ŷi – y ) 2 = (71,69 – 81) 2 = 86,64 .
Możemy zastosować to samo podejście, aby znaleźć regresję sumy kwadratów dla każdego ucznia:
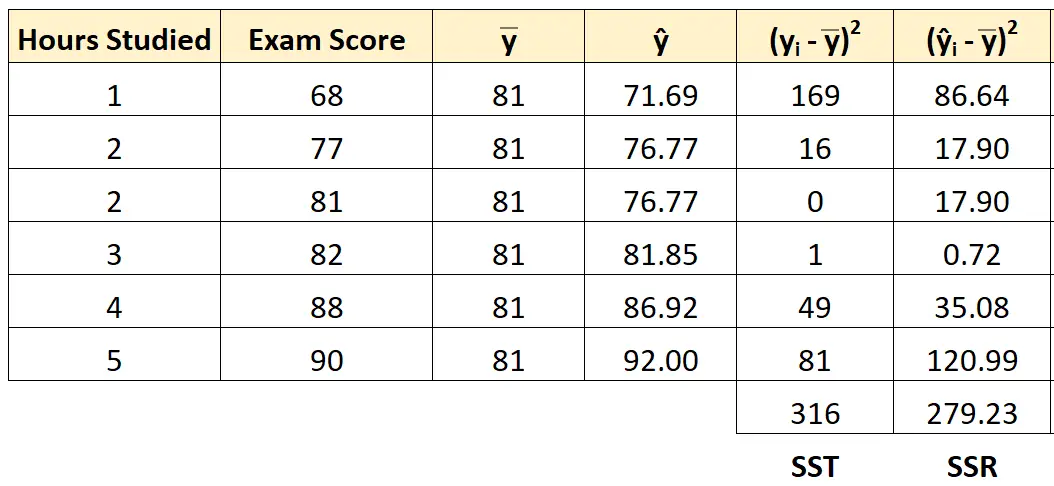
Suma kwadratów regresji wynosi 279,23 .
Krok 5: Oblicz sumę błędów kwadratów (SSE).
Następnie możemy obliczyć błąd sumy kwadratów.
Na przykład suma kwadratów błędu pierwszego ucznia wynosi:
(ŷ ja – y ja ) 2 = (71,69 – 68) 2 = 13,63 .
Możemy zastosować to samo podejście, aby znaleźć sumę kwadratów błędu dla każdego ucznia:
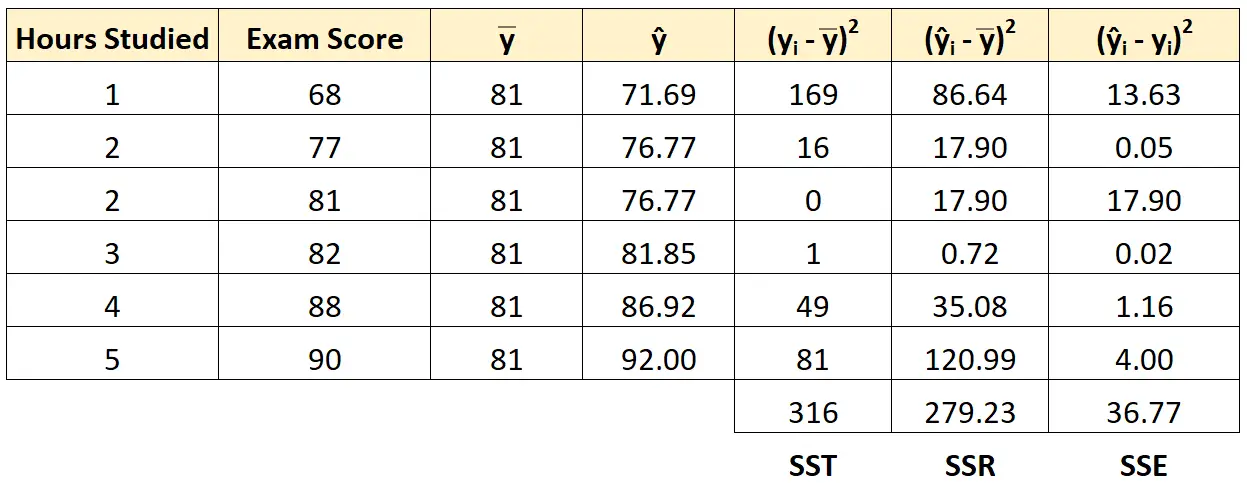
Możemy sprawdzić, że SST = SSR + SSE
- SST = SSR + SSE
- 316 = 279,23 + 36,77
Możemy również obliczyć R kwadrat modelu regresji, korzystając z następującego równania:
- R do kwadratu = SSR / SST
- R do kwadratu = 279,23/316
- R do kwadratu = 0,8836
To mówi nam, że 88,36% różnic w wynikach egzaminów można wyjaśnić liczbą godzin nauki.
Dodatkowe zasoby
Możesz użyć następujących kalkulatorów, aby automatycznie obliczyć SST, SSR i SSE dla dowolnej prostej linii regresji liniowej:
Kalkulator SST
Kalkulator RSS
Kalkulator ESS
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej