Jak utworzyć i zinterpretować krzywą roc w stata

Regresja logistyczna to metoda statystyczna, której używamy do dopasowania modelu regresji, gdy zmienna odpowiedzi jest binarna. Aby ocenić, jak dobrze model regresji logistycznej pasuje do zbioru danych, możemy przyjrzeć się następującym dwóm metrykom:

• Czułość: prawdopodobieństwo, że model przewiduje pozytywny wynik obserwacji, podczas gdy wynik jest rzeczywiście pozytywny.
• Specyficzność: prawdopodobieństwo, że model przewiduje negatywny wynik obserwacji, gdy wynik jest faktycznie negatywny.

Prostym sposobem wizualizacji tych dwóch metryk jest utworzenie krzywej ROC , czyli wykresu przedstawiającego czułość i swoistość modelu regresji logistycznej.

W tym samouczku wyjaśniono, jak utworzyć i zinterpretować krzywą ROC w Stata.

Przykład: krzywa ROC w Stata

W tym przykładzie użyjemy zbioru danych o nazwie lbw , który zawiera następujące zmienne dla 189 matek:

• niska – niezależnie od tego, czy dziecko ma niską masę urodzeniową. 1 = tak, 0 = nie.
• wiek – wiek matki.
• palić – niezależnie od tego, czy matka paliła w czasie ciąży. 1 = tak, 0 = nie.

Do danych dopasujemy model regresji logistycznej, wykorzystując wiek i palenie jako zmienne objaśniające oraz niską masę urodzeniową jako zmienną odpowiedzi. Następnie utworzymy krzywą ROC, aby przeanalizować, jak dobrze model pasuje do danych.

Krok 1: Załaduj i wyświetl dane.

Załaduj dane za pomocą następującego polecenia:

użyj https://www.stata-press.com/data/r13/lbw

Uzyskaj szybkie zrozumienie zbioru danych za pomocą następującego polecenia:

podsumować

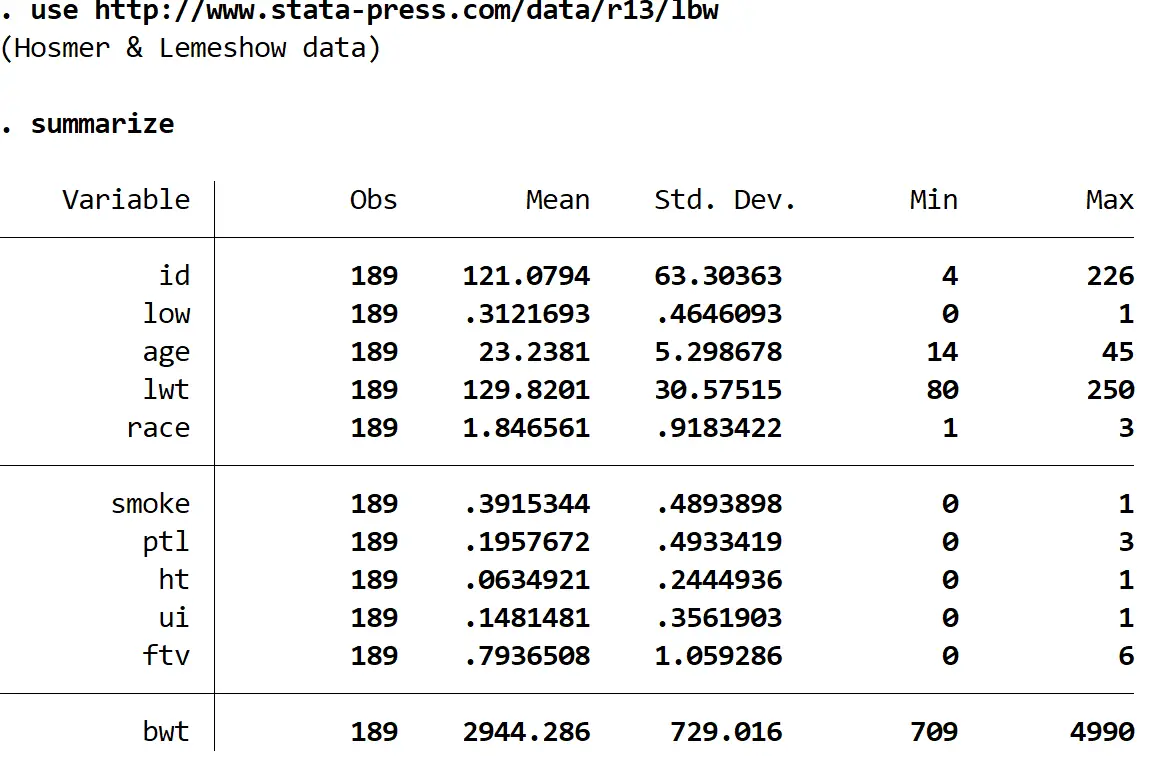
W zbiorze danych znajduje się 11 różnych zmiennych, ale interesują nas tylko trzy: niski poziom, wiek i palenie.

Krok 2: Dopasuj model regresji logistycznej.

Użyj następującego polecenia, aby dopasować model regresji logistycznej:

logit dymny o niskim wieku

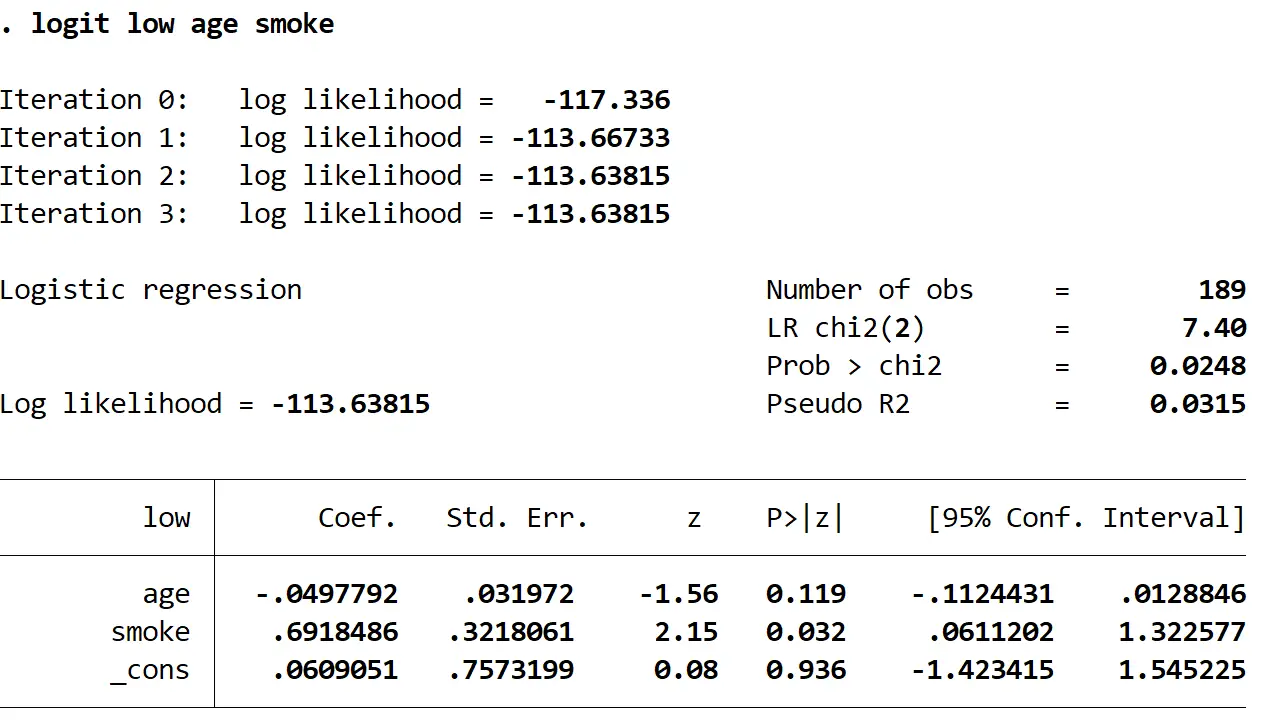
Krok 3: Utwórz krzywą ROC.

Krzywą ROC dla modelu możemy utworzyć za pomocą następującego polecenia:

loc

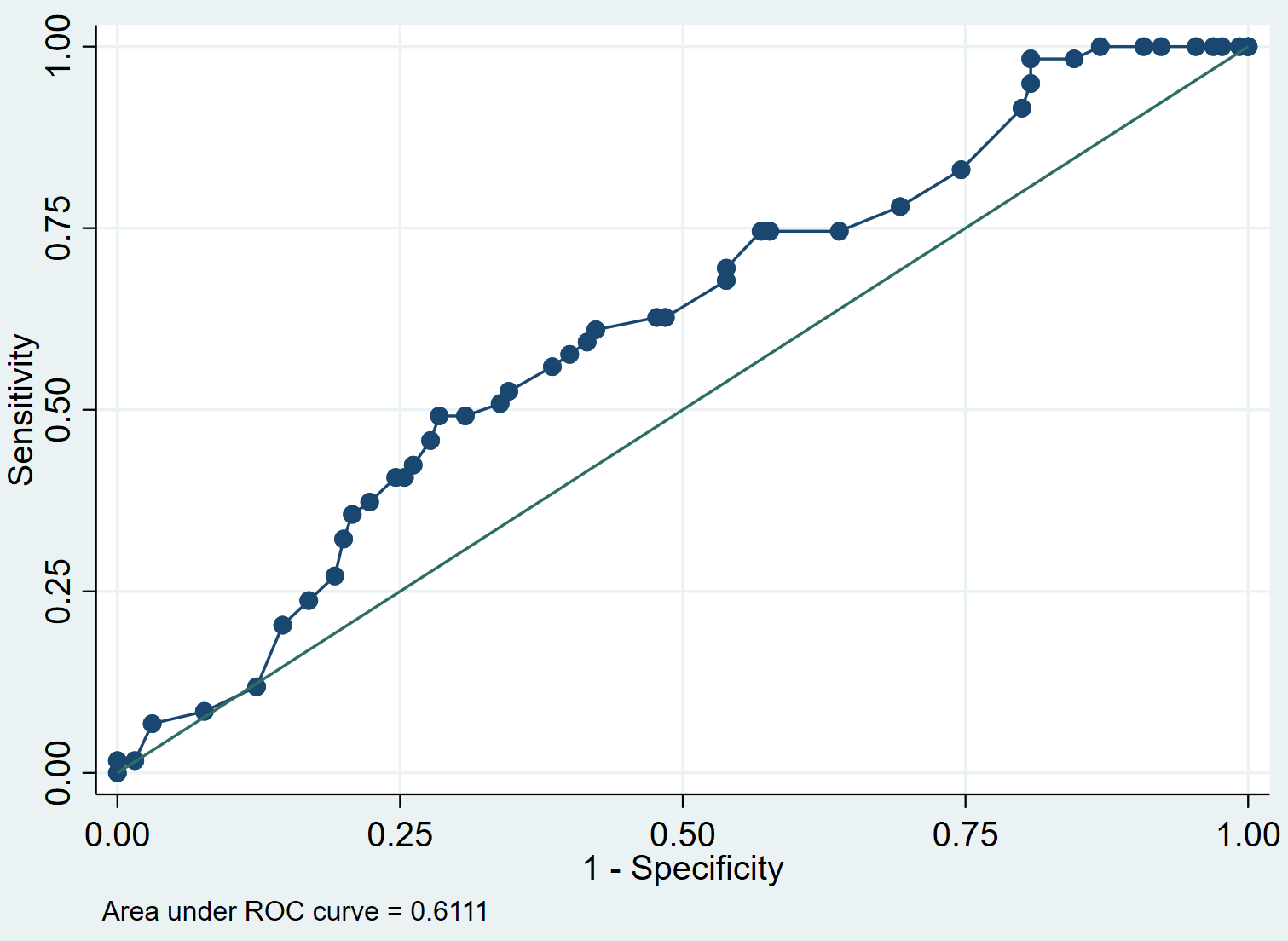
Krok 4: Zinterpretuj krzywą ROC.

Kiedy dopasujemy model regresji logistycznej, można go wykorzystać do obliczenia prawdopodobieństwa, że dana obserwacja będzie miała pozytywny wynik, w oparciu o wartości zmiennych predykcyjnych.

Aby określić, czy obserwacja powinna zostać sklasyfikowana jako dodatnia, możemy wybrać taki próg, że obserwacje z skorygowanym prawdopodobieństwem powyżej progu zostaną sklasyfikowane jako pozytywne, a wszystkie obserwacje z skorygowanym prawdopodobieństwem poniżej progu zostaną sklasyfikowane jako negatywne. .

Załóżmy na przykład, że wybieramy próg 0,5. Oznacza to, że każda obserwacja ze skorygowanym prawdopodobieństwem większym niż 0,5 będzie miała wynik pozytywny, podczas gdy każda obserwacja z skorygowanym prawdopodobieństwem mniejszym lub równym 0,5 będzie miała wynik negatywny.

Krzywa ROC pokazuje nam wartości czułości w porównaniu ze specyficznością 1, gdy wartość progowa zmienia się z 0 na 1. Model o wysokiej czułości i specyficzności będzie miał krzywą ROC, która obejmuje lewy górny róg wykresu. Model o niskiej czułości i niskiej swoistości będzie miał krzywą zbliżoną do przekątnej 45 stopni.

AUC (obszar pod krzywą) daje nam wyobrażenie o zdolności modelu do rozróżnienia wyników pozytywnych i negatywnych. AUC może mieścić się w zakresie od 0 do 1. Im wyższe AUC, tym lepiej model poprawnie klasyfikuje wyniki. W naszym przykładzie widzimy, że AUC wynosi 0,6111 .

Możemy użyć AUC do porównania wydajności dwóch lub więcej modeli. Model z najwyższym AUC sprawdza się najlepiej.

Dodatkowe zasoby

Jak przeprowadzić regresję logistyczną w Stata
Jak interpretować krzywą ROC i AUC modelu regresji logistycznej