Jaki jest błąd standardowy oszacowania? (definicja – przykład)

Błąd standardowy oszacowania jest sposobem pomiaru dokładności przewidywań dokonywanych za pomocą modelu regresji.

Często oznaczane σ _est , oblicza się je w następujący sposób:

σ _is = √ Σ(y – ŷ) ² /n

Złoto:

• y: Obserwowana wartość
• ŷ: Przewidywana wartość
• n: Całkowita liczba obserwacji

Błąd standardowy oszacowania daje nam wyobrażenie o tym, jak dobrze model regresji pasuje do zbioru danych. Zwłaszcza:

• Im mniejsza wartość, tym lepsze dopasowanie.
• Im większa wartość, tym gorsze dopasowanie.

W przypadku modelu regresji z małym błędem standardowym oszacowania punkty danych będą ściśle skupione wokół oszacowanej linii regresji:

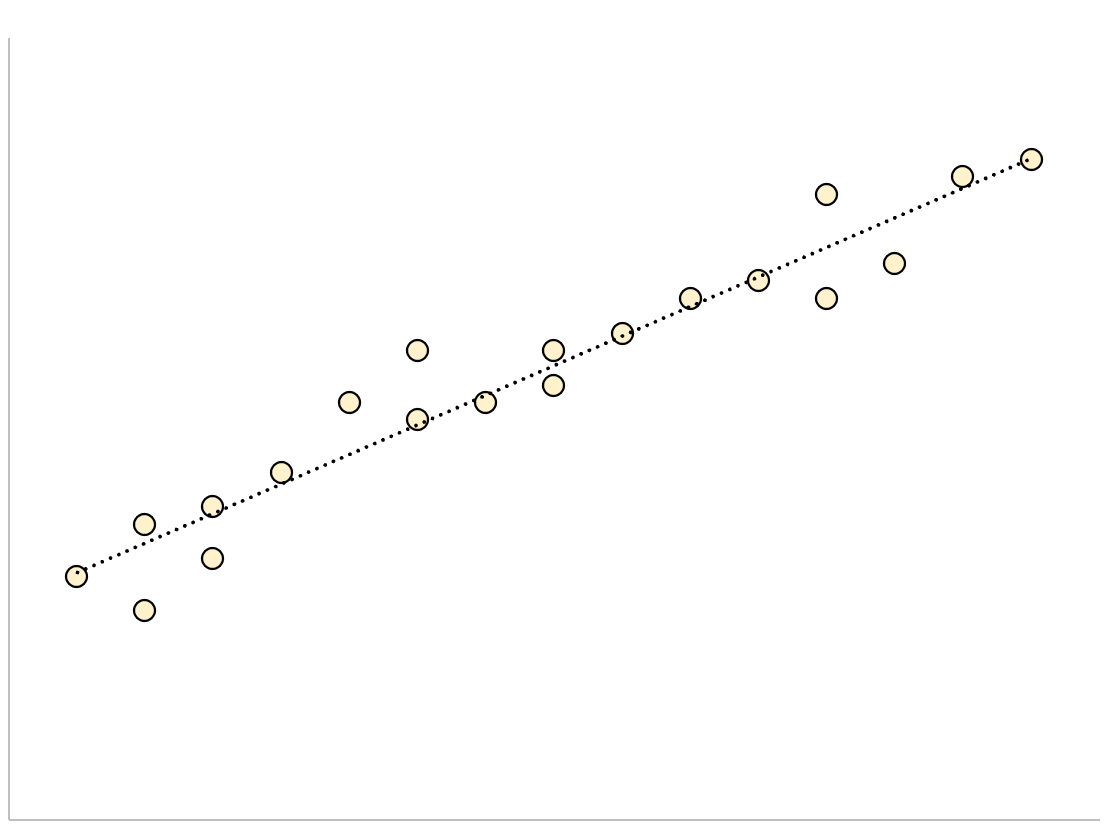
I odwrotnie, w przypadku modelu regresji z dużym błędem standardowym estymacji punkty danych będą luźniej rozproszone wokół linii regresji:

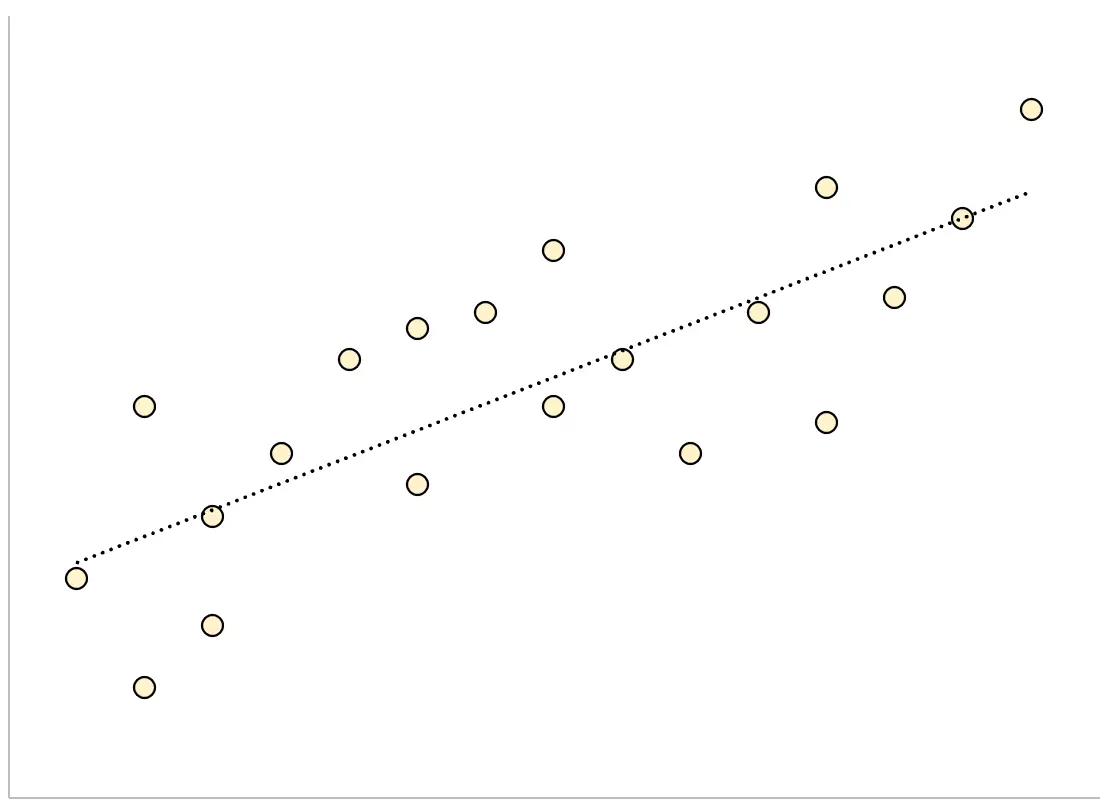
Poniższy przykład pokazuje, jak obliczyć i zinterpretować błąd standardowy oszacowania dla modelu regresji w programie Excel.

Przykład: standardowy błąd oszacowania w Excelu

Wykonaj poniższe kroki, aby obliczyć błąd standardowy oszacowania dla modelu regresji w programie Excel.

Krok 1: Wprowadź dane

Najpierw wprowadź wartości zestawu danych:

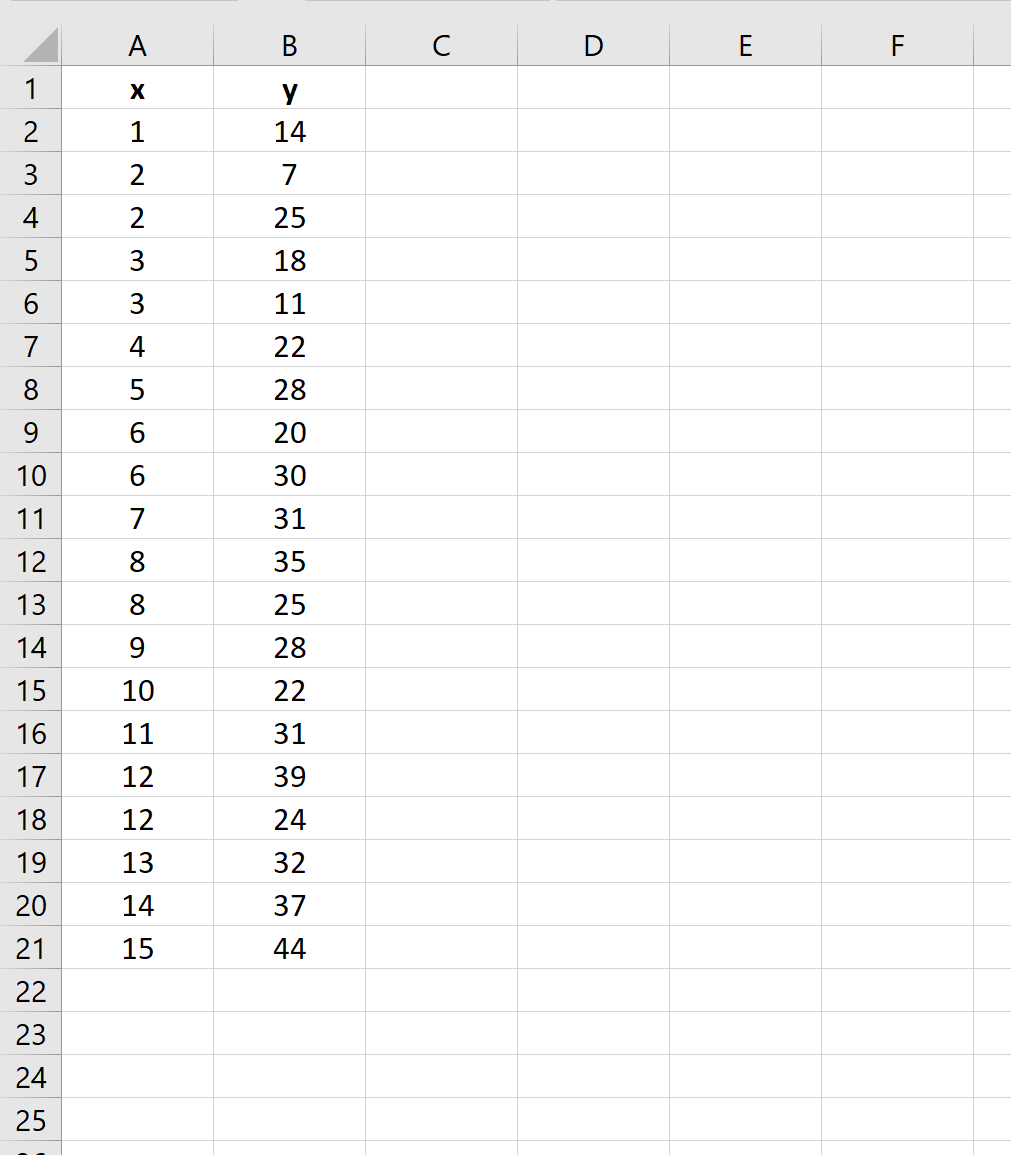
Krok 2: Wykonaj regresję liniową

Następnie kliknij kartę Dane na górnej wstążce. Następnie kliknij opcję Analiza danych w grupie Analizuj .

Jeśli nie widzisz tej opcji, musisz najpierw załadować pakiet Analysis ToolPak .

W nowym oknie, które się pojawi, kliknij Regresja , a następnie kliknij OK .

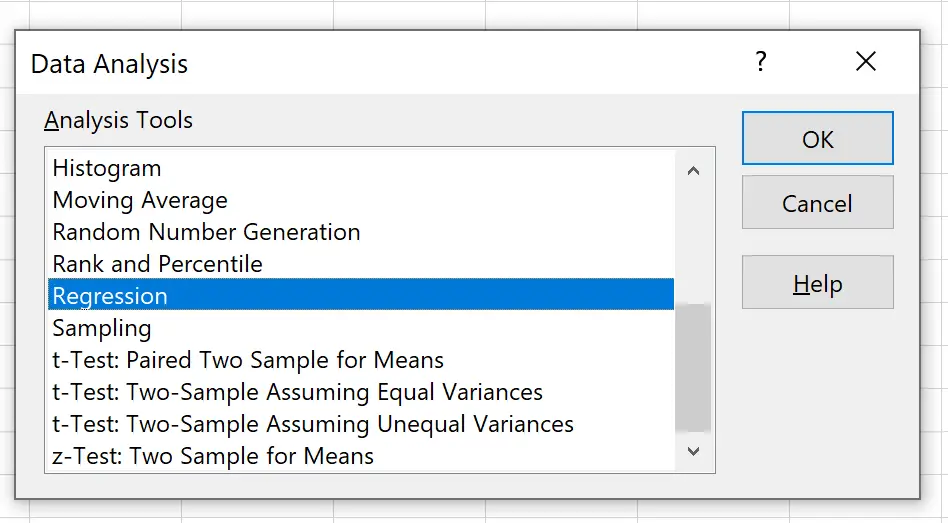
W nowym oknie, które się pojawi, podaj następujące informacje:

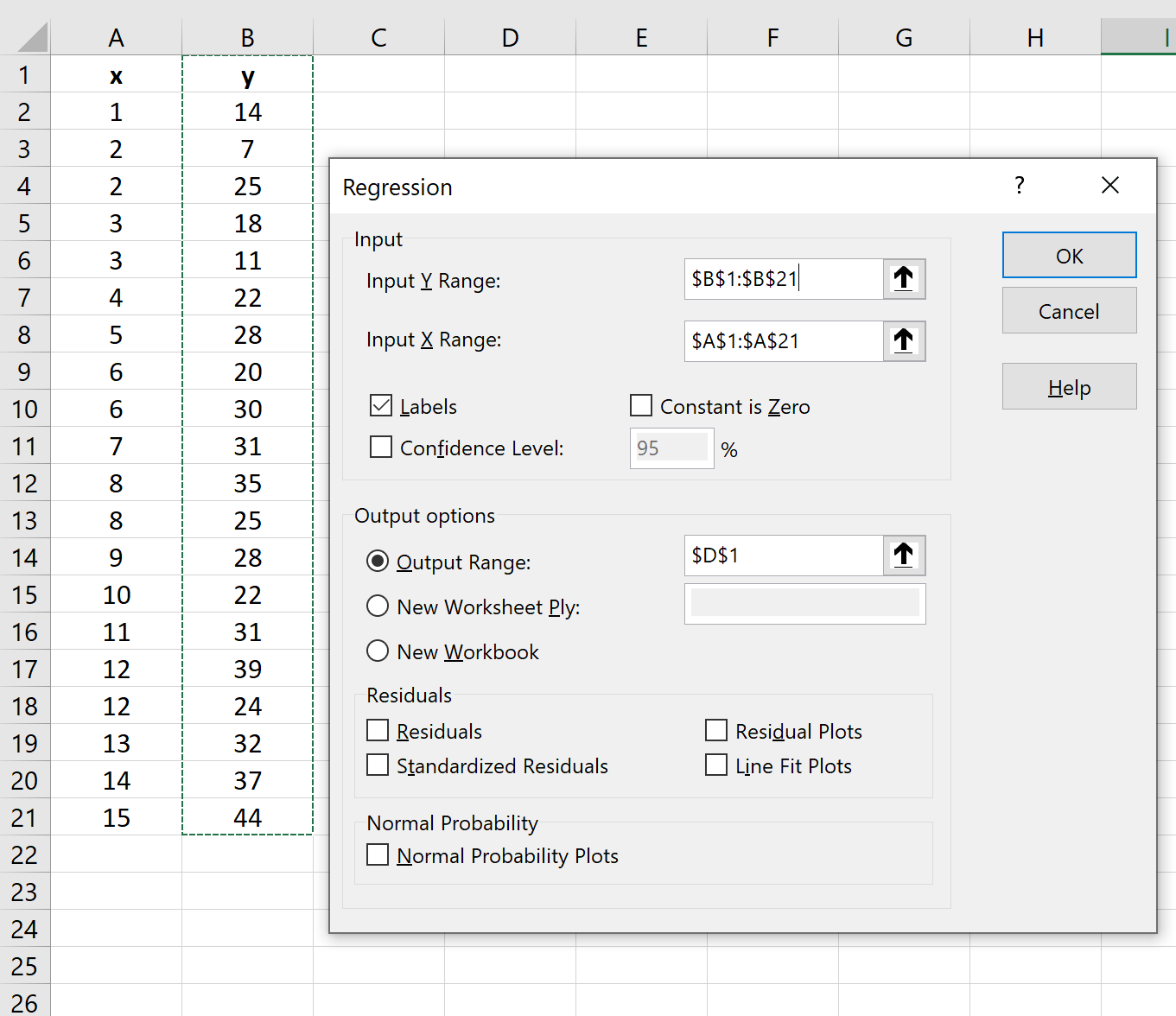
Po kliknięciu OK pojawi się wynik regresji:

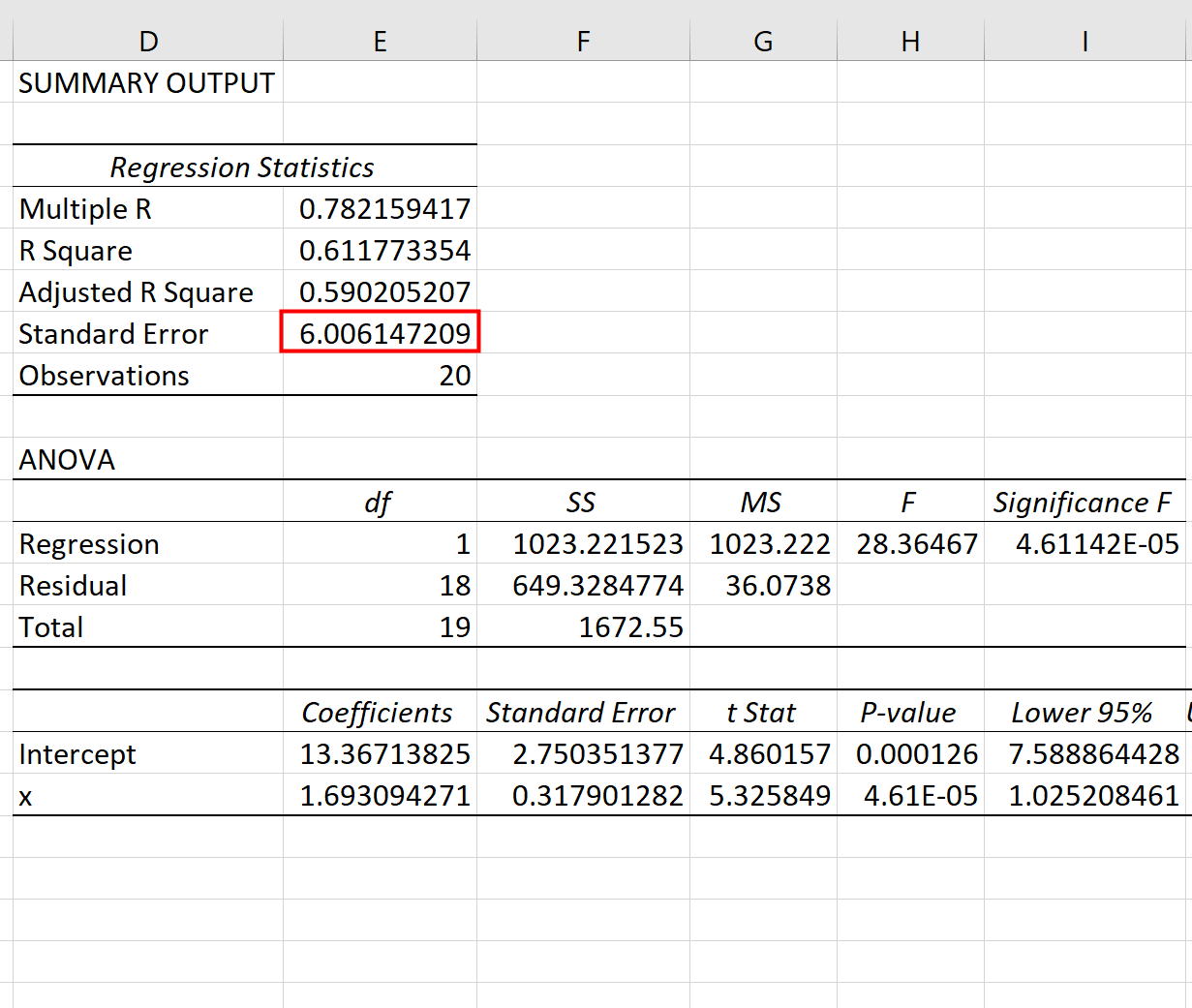
Możemy wykorzystać współczynniki z tabeli regresji do skonstruowania oszacowanego równania regresji:

ŷ = 13,367 + 1,693(x)

Widzimy, że błąd standardowy oszacowania dla tego modelu regresji wynosi 6,006 . Mówiąc prościej, mówi nam to, że średni punkt danych znajduje się 6,006 jednostki od linii regresji.

Możemy użyć oszacowanego równania regresji i błędu standardowego oszacowania, aby skonstruować 95% przedział ufności dla przewidywanej wartości określonego punktu danych.

Załóżmy na przykład, że x równa się 10. Korzystając z oszacowanego równania regresji, możemy przewidzieć, że y będzie równe:

ŷ = 13,367 + 1,693*(10) = 30,297

Możemy uzyskać 95% przedział ufności dla tego oszacowania, korzystając z następującego wzoru:

• 95% CI = [ŷ – 1,96*σ _wynosi , ŷ + 1,96*σ _wynosi ]

W naszym przykładzie 95% przedział ufności zostanie obliczony jako:

• 95% CI = [ŷ – 1,96*σ _wynosi , ŷ + 1,96*σ _wynosi ]
• 95% CI = [30,297 – 1,96*6,006, 30,297 + 1,96*6,006]
• 95% CI = [18 525, 42 069]

Dodatkowe zasoby

Jak wykonać prostą regresję liniową w programie Excel
Jak wykonać wielokrotną regresję liniową w programie Excel
Jak utworzyć wykres resztowy w programie Excel