Standaryzacja czy normalizacja: jaka jest różnica?

Standaryzacja i normalizacja to dwa sposoby zmiany rozmiaru danych.

Normalizacja skaluje zbiór danych tak, aby miał średnią 0 i odchylenie standardowe 1. W tym celu używa następującego wzoru:

x _nowy = (x _i – x ) / s

Złoto:

• x _i : ^i-ta wartość zbioru danych
• x : Przykładowe środki
• s : odchylenie standardowe próbki

Normalizacja zmienia rozmiar zbioru danych tak, aby każda wartość mieściła się w przedziale od 0 do 1. Dokonuje tego za pomocą następującej formuły:

x _nowy = (x _i – x _min ) / (x _max – x _min )

Złoto:

• x _i : ^i-ta wartość zbioru danych
• x _min : Minimalna wartość w zbiorze danych
• x _max : Maksymalna wartość w zbiorze danych

Poniższe przykłady pokazują, jak w praktyce standaryzować i normalizować zbiór danych.

Przykład: Jak standaryzować dane

Załóżmy, że mamy następujący zbiór danych:

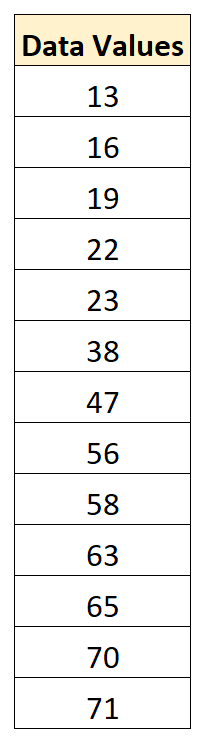
Średnia wartość w zbiorze danych wynosi 43,15, a odchylenie standardowe wynosi 22,13.

Aby znormalizować pierwszą wartość 13 , zastosowalibyśmy udostępnioną wcześniej formułę:

• x _nowy = (x _i – x ) / s = (13 – 43,15) / 22,13 = -1,36

Aby znormalizować drugą wartość 16 , użylibyśmy tego samego wzoru:

• x _nowy = (x _i – x ) / s = (16 – 43,15) / 22,13 = -1,23

Aby znormalizować trzecią wartość 19 , użylibyśmy tego samego wzoru:

• x _nowy = (x _i – x ) / s = (19 – 43,15) / 22,13 = -1,09

Możemy użyć dokładnie tego samego wzoru, aby ujednolicić każdą wartość w oryginalnym zbiorze danych:

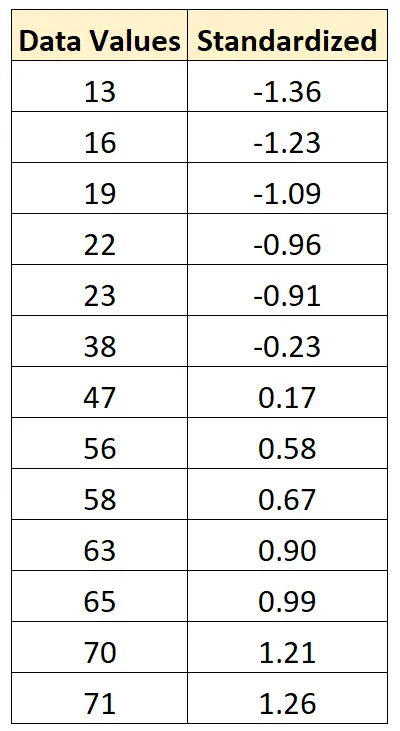
Przykład: Jak normalizować dane

Załóżmy ponownie, że mamy następujący zestaw danych:

Minimalna wartość w zbiorze danych to 13, a maksymalna wartość to 71.

Aby znormalizować pierwszą wartość 13 , zastosowalibyśmy udostępnioną wcześniej formułę:

• x _nowy = (x _i – x _min ) / (x _max – x _min ) = (13 – 13) / (71 – 13) = 0

Aby znormalizować drugą wartość 16 , użylibyśmy tego samego wzoru:

• x _nowy = (x _i – x _min ) / (x _max – x _min ) = (16 – 13) / (71 – 13) = 0,0517

Aby znormalizować trzecią wartość 19 , użylibyśmy tego samego wzoru:

• x _nowy = (x _i – x _min ) / (x _max – x _min ) = (19 – 13) / (71 – 13) = 0,1034

Możemy użyć dokładnie tego samego wzoru, aby znormalizować każdą wartość w oryginalnym zbiorze danych w zakresie od 0 do 1:

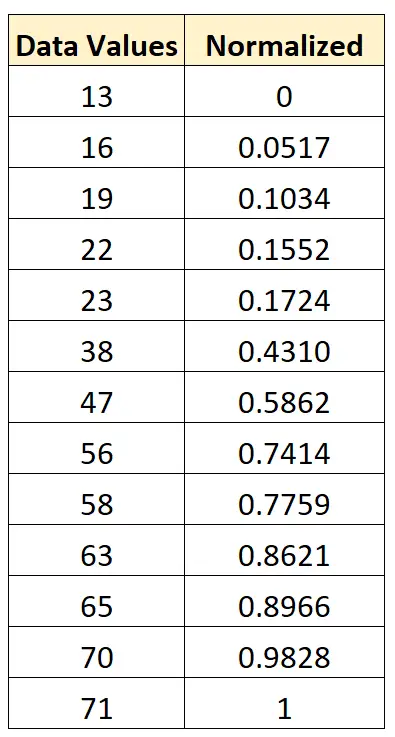
Standaryzacja czy normalizacja: kiedy je stosować?

Zwykle normalizujemy dane, gdy przeprowadzamy analizę, w której mamy wiele zmiennych mierzonych w różnych skalach i chcemy, aby każda ze zmiennych miała ten sam zakres.

Zapobiega to wywieraniu przez jedną zmienną niepożądanego wpływu, zwłaszcza jeśli jest ona mierzona w różnych jednostkach (tzn. jeśli jedna zmienna jest mierzona w calach, a druga w jardach).

Z drugiej strony zazwyczaj normalizujemy dane, gdy chcemy wiedzieć, ile odchyleń standardowych każda wartość w zbiorze danych różni się od średniej.

Na przykład możemy mieć listę wyników egzaminów 500 uczniów w określonej szkole i chcielibyśmy wiedzieć, ile odchyleń standardowych każdy wynik egzaminu od średniego wyniku.

W tym przypadku moglibyśmy znormalizować surowe dane, aby poznać te informacje. Następnie standaryzowany wynik 1,26 powiedziałby nam, że wynik egzaminu tego konkretnego ucznia jest o 1,26 odchylenia standardowego wyższy od średniego wyniku egzaminu.

Niezależnie od tego, czy zdecydujesz się na normalizację, czy standaryzację danych, pamiętaj o następujących kwestiach:

• Znormalizowany zbiór danych zawsze będzie miał wartości od 0 do 1.
• Standaryzowany zestaw danych będzie miał średnią 0 i odchylenie standardowe 1, ale nie ma określonej górnej ani dolnej granicy wartości maksymalnych i minimalnych.

W zależności od konkretnego scenariusza bardziej sensowna może być normalizacja lub standaryzacja danych.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak standaryzować i normalizować dane w różnych programach statystycznych:

Jak normalizować dane w R
Jak normalizować dane w programie Excel
Jak normalizować dane w Pythonie
Jak standaryzować dane w R