Co to jest standaryzowana statystyka testowa?
Hipoteza statystyczna to założenie dotyczące parametru populacji . Na przykład możemy założyć, że średni wzrost mężczyzny w Stanach Zjednoczonych wynosi 70 cali. Hipoteza dotycząca wzrostu jest hipotezą statystyczną , a prawdziwy średni wzrost mężczyzny w Stanach Zjednoczonych jest parametrem populacyjnym .
Test hipotezy to formalny test statystyczny, którego używamy do odrzucenia lub nieodrzucenia hipotezy statystycznej.
Podstawowy proces testowania hipotez wygląda następująco:
1. Zbierz przykładowe dane.
2. Oblicz standaryzowaną statystykę testową dla przykładowych danych.
3. Porównaj standaryzowaną statystykę testową z wartością krytyczną. Jeśli jest bardziej ekstremalna niż wartość krytyczna, odrzuć hipotezę zerową. W przeciwnym razie nie odrzucaj testu hipotezy zerowej.
Wzór, którego używamy do obliczenia standardowej statystyki testowej, różni się w zależności od rodzaju testowania hipotez, które przeprowadzamy.
Poniższa tabela przedstawia wzór, który należy zastosować do obliczenia standaryzowanej statystyki testowej dla każdego z czterech głównych typów testowania hipotez:
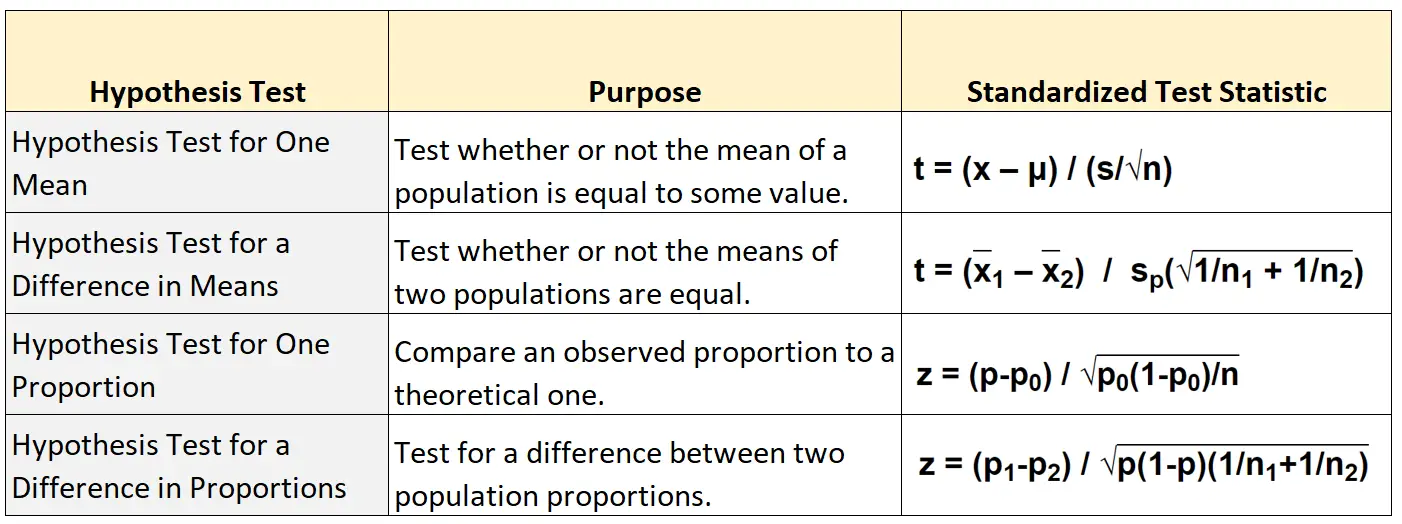
Testowanie hipotez dla średniej
Test t dla jednej próby służy do sprawdzenia, czy średnia populacji jest równa określonej wartości.
Standaryzowaną statystykę testową dla tego typu testu oblicza się w następujący sposób:
t = ( X – μ) / (s/√n)
Złoto:
- x: średnia próbki
- μ 0 : hipotetyczna średnia populacji
- s: odchylenie standardowe próbki
- n: wielkość próbki
W tym samouczku znajdziesz przykład obliczenia tej standardowej statystyki testowej.
Testowanie hipotez dla różnicy średnich
Test t dla dwóch prób służy do sprawdzenia, czy średnie z dwóch populacji są równe, czy nie.
Standaryzowaną statystykę testową dla tego typu testu oblicza się w następujący sposób:
t = ( X 1 – X 2 ) / s p (√ 1/n 1 + 1/n 2 )
gdzie x 1 i x 2 to średnie próbki, n 1 i n 2 to liczebność próby, a sp oblicza się w następujący sposób:
s p = √ (n 1 -1) s 1 2 + (n 2 -1) s 2 2 / (n 1 + n 2 -2)
gdzie s 1 2 i s 2 2 są wariancjami próbki.
W tym samouczku znajdziesz przykład obliczenia tej standardowej statystyki testowej.
Testowanie hipotez dla proporcji
Do porównania zaobserwowanej proporcji z teoretyczną proporcją stosuje się test z jednej proporcji .
Standaryzowaną statystykę testową dla tego typu testu oblicza się w następujący sposób:
z = (pp 0 ) / √ p 0 (1-p 0 )/n
Złoto:
- p: obserwowana proporcja próbki
- p 0 : hipotetyczny odsetek populacji
- n: wielkość próbki
W tym samouczku znajdziesz przykład obliczenia tej standardowej statystyki testowej.
Testowanie hipotezy dla różnicy proporcji
Test Z dwóch proporcji służy do sprawdzania różnicy między dwiema proporcjami populacji.
Standaryzowaną statystykę testową dla tego typu testu oblicza się w następujący sposób:
z = (p 1 -p 2 ) / √ p(1-p)(1/n 1 +1/n 2 )
gdzie p 1 i p 2 to proporcje próbek, n 1 i n 2 to liczebność próbek, a p to całkowity udział zbiorczy obliczony w następujący sposób:
p = (p 1 n 1 + p 2 n 2 )/(n 1 + n 2 )
W tym samouczku znajdziesz przykład obliczenia tej standardowej statystyki testowej.
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej