Jak wykonać regresję kwadratową w stata

Kiedy dwie zmienne są ze sobą powiązane liniowo, często można zastosować prostą regresję liniową do ilościowego określenia ich związku.

Jeśli jednak dwie zmienne mają związek kwadratowy, do ilościowego określenia ich związku można zastosować regresję kwadratową .

W tym samouczku wyjaśniono, jak przeprowadzić regresję kwadratową w programie Stata.

Przykład: regresja kwadratowa w Stata

Załóżmy, że chcemy zrozumieć związek pomiędzy liczbą przepracowanych godzin a szczęściem. Mamy następujące dane dotyczące liczby godzin przepracowanych tygodniowo i raportowanego poziomu szczęścia (w skali od 0 do 100) dla 16 różnych osób:

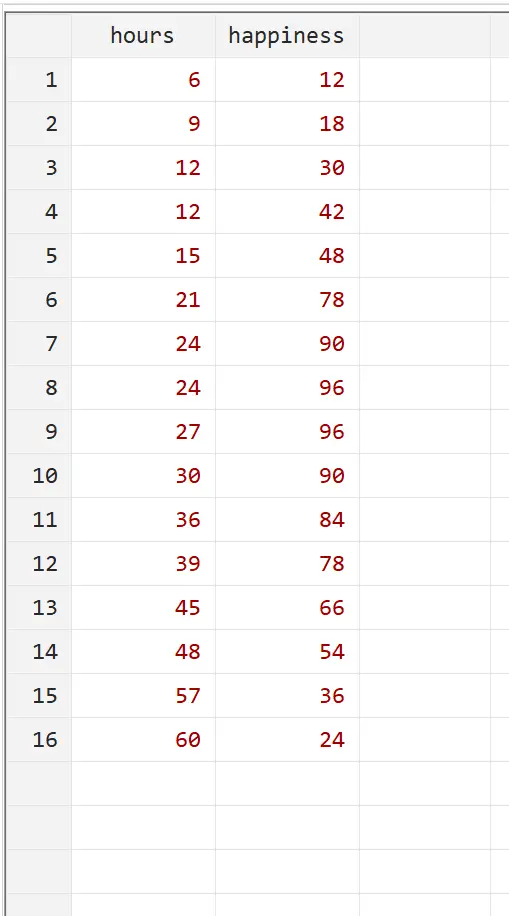
Możesz odtworzyć ten przykład, wprowadzając dokładnie te dane do Stata, używając opcji Dane > Edytor danych > Edytor danych (Edytuj) w górnym menu.

Wykonaj poniższe kroki, aby wykonać regresję kwadratową w programie Stata.

Krok 1: Wizualizuj dane.

Zanim będziemy mogli zastosować regresję kwadratową, musimy upewnić się, że związek między zmienną objaśniającą (godziny) a zmienną odpowiedzi (szczęście) jest rzeczywiście kwadratowy. Zwizualizujmy więc dane za pomocą wykresu rozrzutu , wpisując następujące polecenie w polu Polecenie:

rozproszyć godziny szczęścia

Daje to następujący wykres punktowy:

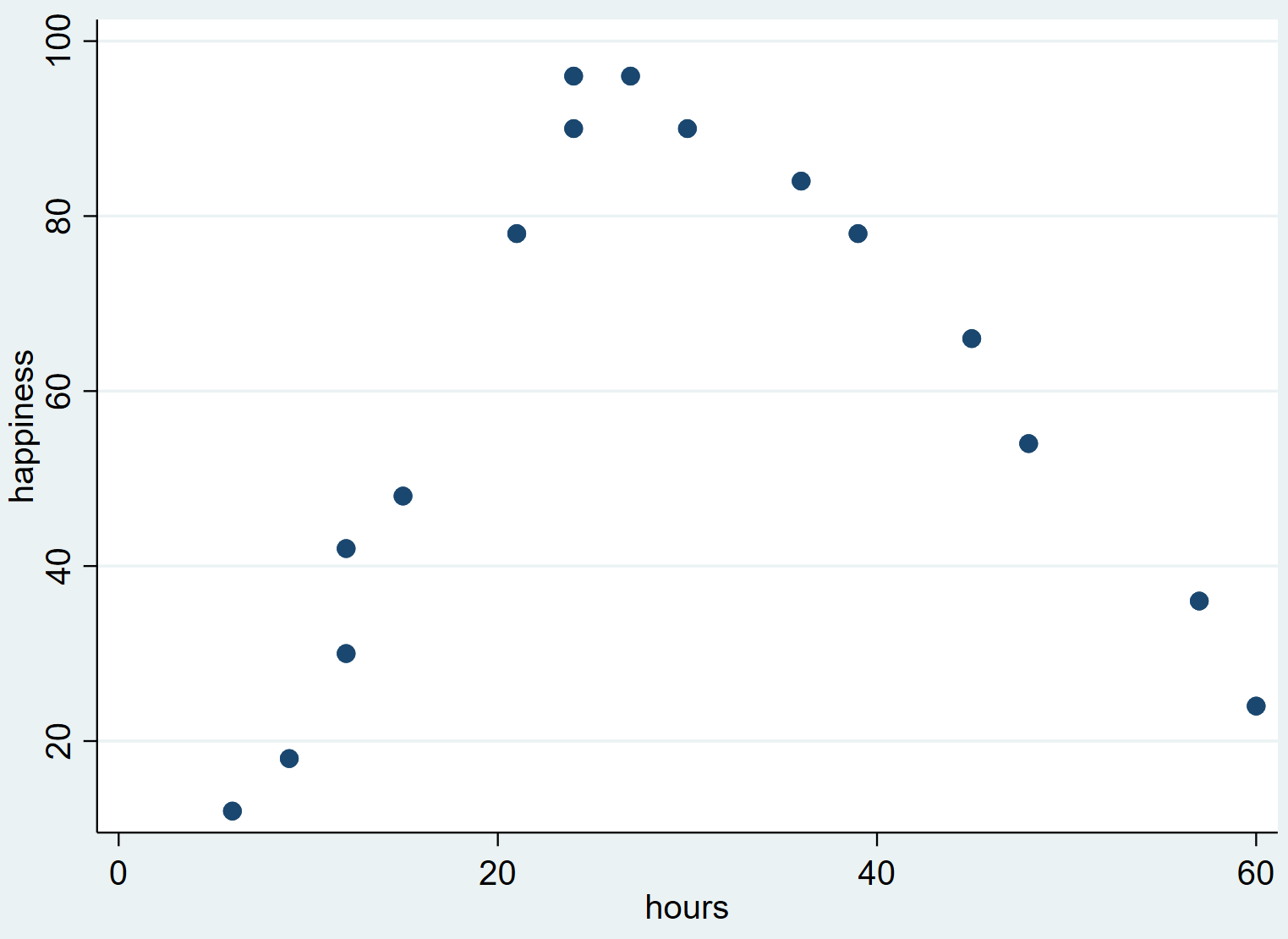
Widzimy, że szczęście ma tendencję do wzrostu, gdy liczba przepracowanych godzin wzrasta od zera do pewnego punktu, ale następnie zaczyna spadać, gdy liczba przepracowanych godzin przekracza około 30.

Ten odwrócony kształt litery „U” na wykresie rozrzutu wskazuje, że istnieje związek kwadratowy między przepracowanymi godzinami a szczęściem, co oznacza, że do ilościowego określenia tej zależności powinniśmy użyć regresji kwadratowej.

Krok 2: Wykonaj regresję kwadratową.

Przed dopasowaniem modelu regresji kwadratowej do danych musimy utworzyć nową zmienną dla kwadratów wartości naszej zmiennej predykcyjnej godzin . Możemy to zrobić wpisując w polu Polecenie:

gen godziny2 = godziny*godziny

Możemy wyświetlić tę nową zmienną, przechodząc do Dane > Edytor danych > Edytor danych (Przeglądaj) z górnego menu.

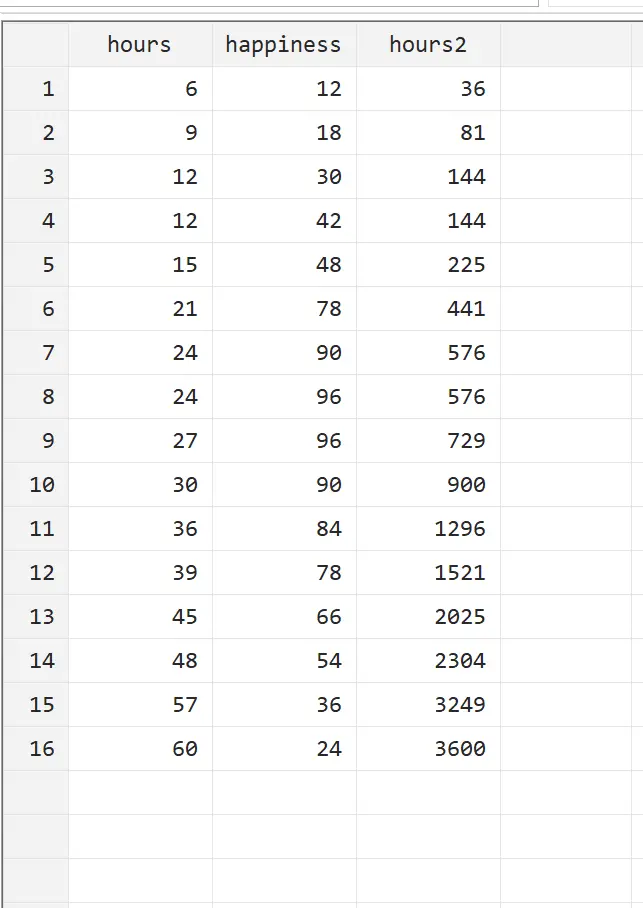
Widzimy, że godzina2 to po prostu godziny do kwadratu. Możemy teraz przeprowadzić regresję kwadratową, używając godzin i godzin2 jako zmiennych objaśniających oraz szczęścia jako zmiennej odpowiedzi. Aby wykonać regresję kwadratową, wpisz następujące polecenie w polu Polecenie:

godziny regresu godzin szczęścia 2

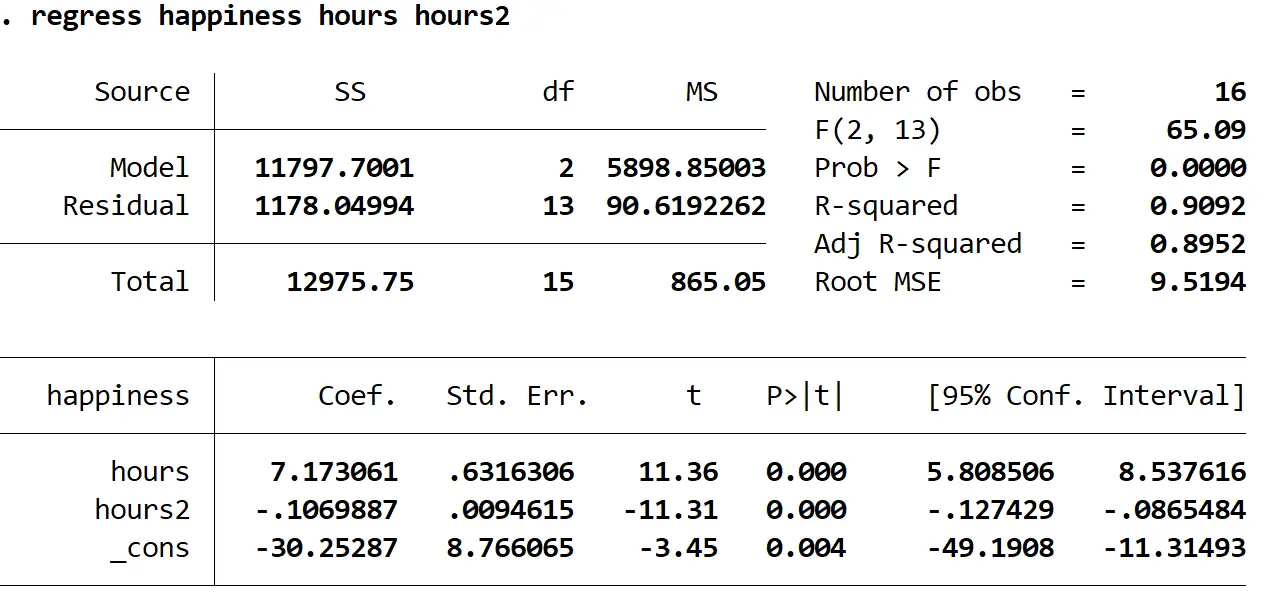
Oto jak zinterpretować najciekawsze liczby w wyniku:

Prawdopodobieństwo > F: 0,000. Jest to wartość p dla ogólnej regresji. Ponieważ wartość ta jest mniejsza niż 0,05, oznacza to, że zmienne predykcyjne godziny i godziny ² łącznie mają statystycznie istotny związek ze zmienną odpowiedzi szczęście .

R do kwadratu: 0,9092. Jest to proporcja wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennej objaśniającej. W tym przykładzie 90,92% zmian w szczęściu można wytłumaczyć godzinami ² .

Równanie regresji: Możemy utworzyć równanie regresji, korzystając z wartości współczynników pokazanych w tabeli wyjściowej. W tym przypadku równanie wyglądałoby następująco:

przewidywane szczęście = -30,25287 + 7,173061 (godziny) – 0,1069887 ( ² godziny)

Możemy użyć tego równania, aby znaleźć przewidywane szczęście danej osoby, biorąc pod uwagę liczbę godzin przepracowanych w tygodniu.

Na przykład osoba pracująca 60 godzin tygodniowo powinna mieć poziom szczęścia 14,97:

przewidywane szczęście = -30,25287 + 7,173061(60) – 0,1069887(60 ² ) = 14,97 .

I odwrotnie, osoba pracująca 30 godzin tygodniowo powinna mieć poziom szczęścia na poziomie 88,65:

przewidywane szczęście = -30,25287 + 7,173061(30) – 0,1069887(30 ² ) = 88,65 .

Krok 3: Ogłoś wyniki.

Na koniec chcemy zgłosić wyniki naszej regresji kwadratowej. Oto przykład, jak to zrobić:

Przeprowadzono regresję kwadratową, aby określić ilościowo związek między liczbą godzin przepracowanych przez daną osobę a odpowiadającym jej poziomem szczęścia (mierzonym od 0 do 100). Do analizy wykorzystano próbę 16 osób.

Wyniki wykazały, że istnieje istotna statystycznie zależność pomiędzy zmiennymi objaśniającymi godziny i godziny ² a zmienną odpowiedzi szczęście (F(2, 13) = 65,09, p < 0,0001).

Łącznie te dwie zmienne objaśniające odpowiadały za 90,92% wyjaśnionej zmienności szczęścia.

Równanie regresji okazało się następujące:

przewidywane szczęście = -30,25287 + 7,173061 (godziny) – 0,1069887 ( ² godziny)