Jak przetestować normalność w stata

Wiele testów statystycznych wymaga, aby jedna lub więcej zmiennych miało rozkład normalny , aby wyniki testów były wiarygodne.

W tym samouczku wyjaśniono kilka metod, których można użyć do sprawdzenia normalności między zmiennymi w Stata.

Dla każdej z tych metod użyjemy wbudowanego zbioru danych Stata o nazwie auto . Możesz załadować ten zestaw danych za pomocą następującego polecenia:

automatyczne korzystanie z systemu

Metoda 1: histogramy

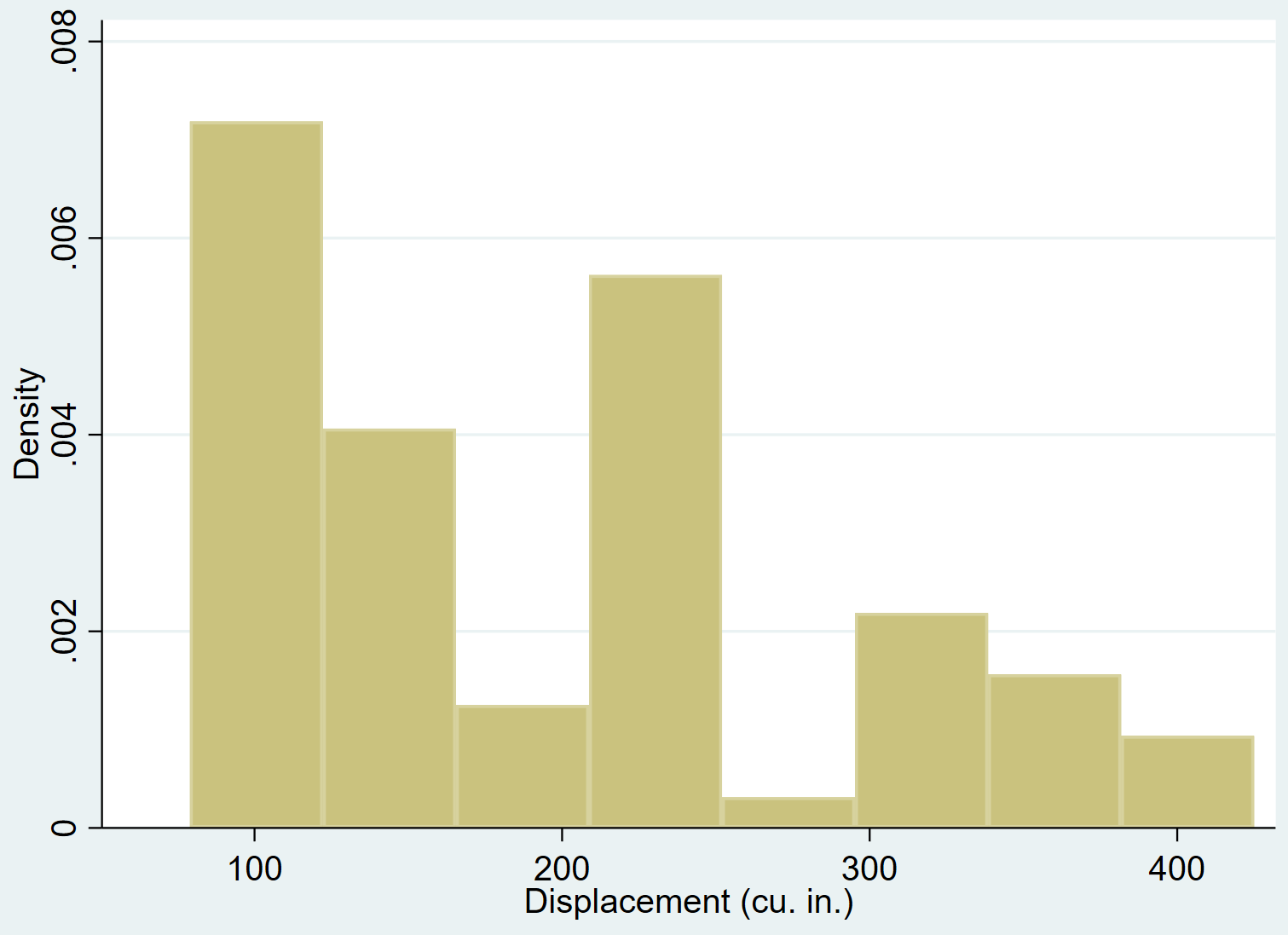
Nieformalnym sposobem sprawdzenia, czy zmienna ma rozkład normalny, jest utworzeniehistogramu przedstawiającego rozkład zmiennej.

Jeżeli zmienna ma rozkład normalny, histogram powinien mieć kształt „dzwonu” z większą liczbą wartości znajdujących się w pobliżu środka i mniejszą liczbą wartości znajdujących się na końcach.

Możemy użyć polecenia hist , aby utworzyć histogram dla przemieszczenia zmiennej:

poruszająca historia

Możemy dodać krzywą gęstości normalnej do histogramu za pomocą polecenia normal :

poruszająca historia, to normalne

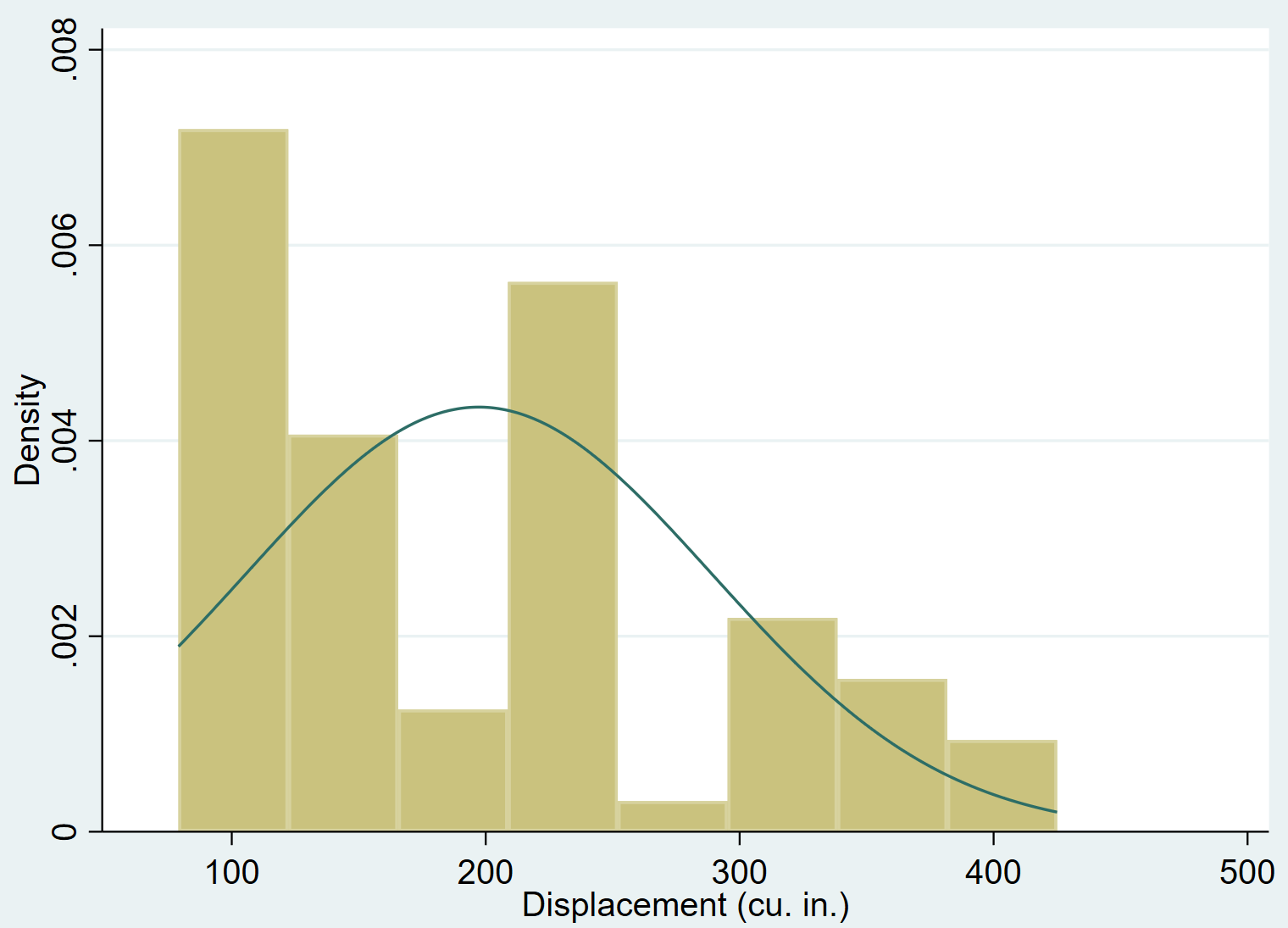
Jest całkiem oczywiste, że przesunięcie zmiennej jest przesunięte w prawo (np. większość wartości koncentruje się po lewej stronie, a długi „ogon” wartości rozciąga się w prawo) i nie ma rozkładu normalnego.

Powiązane: Rozkłady skośne w lewo i w prawo

Metoda 2: Test Shapiro-Wilka

Formalnym sposobem sprawdzenia normalności jest użycie testu Shapiro-Wilka .

Hipotezą zerową dla tego testu jest to, że zmienna ma rozkład normalny. Jeśli wartość p testu jest poniżej pewnego poziomu istotności (najczęściej wybierane wartości to 0,01, 0,05 i 0,10), wówczas możemy odrzucić hipotezę zerową i stwierdzić, że istnieją wystarczające dowody, aby stwierdzić, że zmienna nie ma rozkładu normalnego .

*Ten test można zastosować, gdy całkowita liczba obserwacji wynosi od 4 do 2000.

Możemy użyć polecenia swilk , aby wykonać test Shapiro-Wilka na zmiennym przemieszczeniu :

płynny ruch

Oto jak zinterpretować wynik testu:

Obs: 74. Jest to liczba obserwacji wykorzystanych w teście.

Sz: 0,92542. To jest statystyka testowa dla testu.

Prawdopodobieństwo>z: 0,00031. Jest to wartość p powiązana ze statystyką testową.

Ponieważ wartość p jest mniejsza niż 0,05, możemy odrzucić hipotezę zerową testu. Mamy wystarczające dowody, aby stwierdzić, że zmienne przemieszczenie nie ma rozkładu normalnego.

Możemy także wykonać test Shapiro-Wilka na wielu zmiennych jednocześnie, wypisując wiele zmiennych po poleceniu swilk :

długość przemieszczenia swilk w mpg

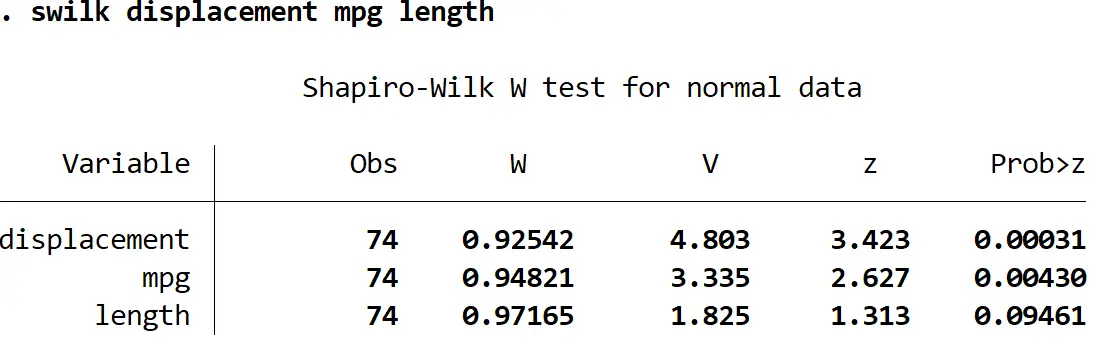
Stosując poziom istotności 0,05, doszlibyśmy do wniosku, że przemieszczenie i mpg nie mają rozkładu normalnego, ale nie mamy wystarczających dowodów, aby stwierdzić, że długość nie ma rozkładu normalnego.

Metoda 3: Test Shapiro-Francii

Innym formalnym sposobem sprawdzenia normalności jest użycie testu Shapiro-Francia .

Hipotezą zerową dla tego testu jest to, że zmienna ma rozkład normalny. Jeśli wartość p testu jest poniżej pewnego poziomu istotności, wówczas możemy odrzucić hipotezę zerową i stwierdzić, że istnieją wystarczające dowody, aby stwierdzić, że zmienna nie ma rozkładu normalnego.

*Ten test można zastosować, gdy całkowita liczba obserwacji wynosi od 10 do 5000.

Możemy użyć polecenia sfrancia , aby wykonać test Shapiro-Wilka na zmiennym przemieszczeniu :

poruszająca się Sfrancia

Oto jak zinterpretować wynik testu:

Obs: 74. Jest to liczba obserwacji wykorzystanych w teście.

W’: 0,93011. To jest statystyka testowa dla testu.

Prawdopodobieństwo>z: 0,00094. Jest to wartość p powiązana ze statystyką testową.

Ponieważ wartość p jest mniejsza niż 0,05, możemy odrzucić hipotezę zerową testu. Mamy wystarczające dowody, aby stwierdzić, że zmienne przemieszczenie nie ma rozkładu normalnego.

Podobnie jak w przypadku testu Shapiro-Wilka, test Shapiro-Francii można wykonać na wielu zmiennych jednocześnie, podając wiele zmiennych po poleceniu sfrancia .

Metoda 4: badanie skośności i kurtozy

Innym sposobem sprawdzenia normalności jest użycie testu skośności i kurtozy , który określa, czy skośność i kurtoza zmiennej są zgodne z rozkładem normalnym.

Hipotezą zerową dla tego testu jest to, że zmienna ma rozkład normalny. Jeśli wartość p testu jest poniżej pewnego poziomu istotności, wówczas możemy odrzucić hipotezę zerową i stwierdzić, że istnieją wystarczające dowody, aby stwierdzić, że zmienna nie ma rozkładu normalnego.

*Ten test wymaga minimum 8 obserwacji.

Możemy użyć polecenia sktest , aby przeprowadzić test skośności i kurtozy zmiennej przemieszczenia :

przesuwanie testu

Oto jak zinterpretować wynik testu:

Obs: 74. Jest to liczba obserwacji wykorzystanych w teście.

przym chi(2): 5,81. To jest statystyka testu chi-kwadrat dla testu.

Prawdopodobne>chi2: 0,0547. Jest to wartość p powiązana ze statystyką testową.

Ponieważ wartość p jest nie mniejsza niż 0,05, nie udaje nam się odrzucić hipotezy zerowej testu. Nie mamy wystarczających dowodów, aby stwierdzić, że ruchy nie mają rozkładu normalnego.

Podobnie jak w przypadku innych testów normalności, można przeprowadzić test skośności i kurtozy na wielu zmiennych jednocześnie, wypisując wiele zmiennych po poleceniu sktest .