Czym jest błąd przewidywania w statystyce? (definicja i przykłady)

W statystyce błąd przewidywania odnosi się do różnicy między wartościami przewidywanymi przez niektóre modele a wartościami rzeczywistymi.

Błąd przewidywania jest często używany w dwóch kontekstach:

1. Regresja liniowa: stosowana do przewidywania wartości ciągłej zmiennej odpowiedzi.

Zwykle mierzymy błąd przewidywania modelu regresji liniowej za pomocą metryki znanej jako RMSE , która oznacza średni błąd kwadratowy.

Oblicza się go w następujący sposób:

RMSE = √ Σ(ŷ _ja – y _ja ) ² / n

Złoto:

• Σ to symbol oznaczający „sumę”
• ŷ _i jest przewidywaną wartością i- ^tej obserwacji
• y _i jest wartością obserwowaną dla ^i-tej obserwacji
• n to wielkość próbki

2. Regresja logistyczna: stosowana do przewidywania wartości binarnej zmiennej odpowiedzi.

Powszechnym sposobem pomiaru błędu przewidywania modelu regresji logistycznej jest użycie metryki zwanej całkowitym współczynnikiem błędów klasyfikacji.

Oblicza się go w następujący sposób:

Całkowity współczynnik błędnych klasyfikacji = (# niepoprawnych przewidywań / # wszystkich przewidywań)

Im niższa wartość współczynnika błędnych klasyfikacji, tym lepiej model jest w stanie przewidzieć wyniki zmiennej odpowiedzi.

Poniższe przykłady pokazują, jak w praktyce obliczyć błąd predykcji dla modelu regresji liniowej i modelu regresji logistycznej.

Przykład 1: Obliczanie błędu przewidywania w regresji liniowej

Załóżmy, że używamy modelu regresji, aby przewidzieć, ile punktów zdobędzie 10 graczy w meczu koszykówki.

Poniższa tabela przedstawia punkty przewidywane przez model w porównaniu z rzeczywistymi punktami zdobytymi przez graczy:

Obliczamy błąd średniokwadratowy (RMSE) w następujący sposób:

• RMSE = √ Σ(ŷ _ja – y _ja ) ² / n
• RMSE = √(((14-12) ² +(15-15) ² +(18-20) ² +(19-16) ² +(25-20) ² +(18-19) ² +(12- 16) ² +(12-20) ² +(15-16) ² +(22-16) ² ) / 10)
• RMSE = 4

Średni błąd kwadratowy wynosi 4. Mówi nam to, że średnie odchylenie między przewidywanymi zdobytymi punktami a faktycznie zdobytymi punktami wynosi 4.

Powiązane: Co jest uważane za dobrą wartość RMSE?

Przykład 2: Obliczanie błędu predykcji w regresji logistycznej

Załóżmy, że używamy modelu regresji logistycznej do przewidzenia, czy 10 koszykarzy z college’u zostanie powołanych do NBA.

Poniższa tabela przedstawia przewidywany wynik każdego gracza w porównaniu z rzeczywistym wynikiem (1 = wybrany, 0 = niewybrany):

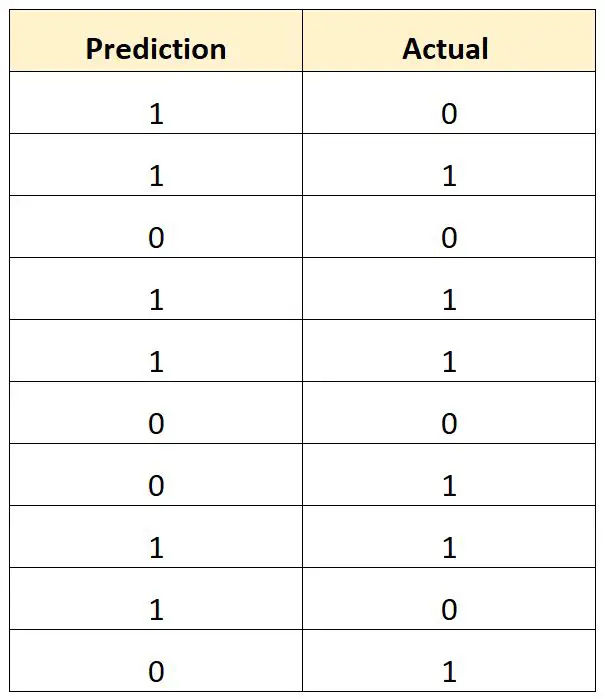
Całkowity współczynnik błędnych klasyfikacji obliczylibyśmy w następujący sposób:

• Całkowity współczynnik błędnych klasyfikacji = (# błędnych przewidywań / # wszystkich przewidywań)
• Całkowity poziom błędu klasyfikacji = 4/10
• Całkowity odsetek błędnych klasyfikacji = 40%

Całkowity poziom błędu klasyfikacji wynosi 40% .

Wartość ta jest dość wysoka, co wskazuje, że model nie radzi sobie zbyt dobrze z przewidywaniem, czy zawodnik zostanie wybrany, czy nie.

Dodatkowe zasoby

Poniższe samouczki stanowią wprowadzenie do różnych typów metod regresji:

Wprowadzenie do prostej regresji liniowej
Wprowadzenie do wielokrotnej regresji liniowej
Wprowadzenie do regresji logistycznej