Co to jest funkcja masy prawdopodobieństwa (pmf) w statystyce?

Funkcja masy prawdopodobieństwa , często w skrócie PMF , mówi nam o prawdopodobieństwie, że dyskretna zmienna losowa przyjmie określoną wartość.

Załóżmy na przykład, że rzucamy kostką raz. Jeśli pozwolimy, aby x oznaczało liczbę, na której wyląduje kość, wówczas prawdopodobieństwo, że x będzie równe różnym wartościom, można opisać w następujący sposób:

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

Prawdopodobieństwo, że kostka wyląduje na dowolnej liczbie od 1 do 6, jest równe.

Oto jak zapisalibyśmy te prawdopodobieństwa jako funkcję masy prawdopodobieństwa:

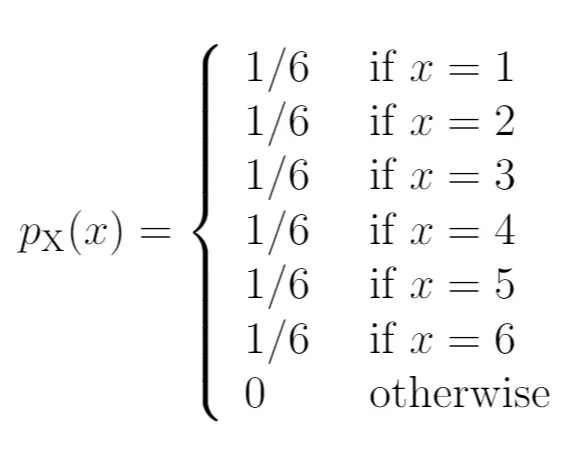
Lewa strona diagramu pokazuje prawdopodobieństwo związane z wynikami po prawej stronie:

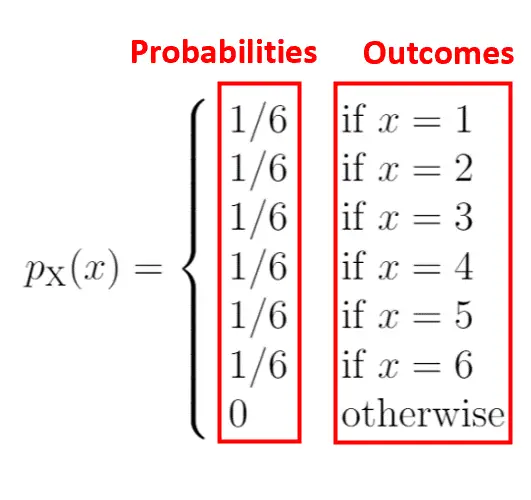
Cechą funkcji masy prawdopodobieństwa jest to, że wszystkie prawdopodobieństwa muszą sumować się do 1. Zauważysz, że ten PMF spełnia ten warunek:

Suma prawdopodobieństw = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

Obsługa funkcji masy prawdopodobieństwa odnosi się do zbioru wartości, jakie może przyjąć dyskretna zmienna losowa. W tym przykładzie wsparcie wyniesie {1, 2, 3, 4, 5, 6}, ponieważ wartość kostki może przyjąć dowolną z tych wartości.

Poza wsparciem wartość PMF wynosi zero. Na przykład prawdopodobieństwo, że kość wypadnie na „0”, „7” lub „8” wynosi zero, ponieważ żadna z tych liczb nie jest uwzględniona w nawiasie.

Funkcje masy prawdopodobieństwa w praktyce

Dwa najczęstsze przykłady funkcji masy prawdopodobieństwa w praktyce dotyczą rozkładu dwumianowego i rozkładu Poissona .

Rozkład dwumianowy

Jeśli zmienna losowa X ma rozkład dwumianowy, prawdopodobieństwo, że X = k powodzenia można obliczyć za pomocą następującego wzoru:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Złoto:

• n: liczba prób
• k: liczba sukcesów
• p: prawdopodobieństwo sukcesu w danej próbie
• _n C _k : liczba sposobów uzyskania k sukcesów w n próbach

Załóżmy na przykład, że rzucamy monetą 3 razy. Możemy użyć powyższego wzoru, aby określić prawdopodobieństwo uzyskania 0, 1, 2 i 3 orłów w tych 3 rzutach:

• P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125
• P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 1 * 1 * (0,5) ² = 0,375
• P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 1 * 1 * (0,5) ¹ = 0,375
• P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 1 * (0,5) ⁰ = 0,125

Dystrybucja ryb

Jeśli zmienna losowa X ma rozkład Poissona, prawdopodobieństwo, że X = k powodzenia można obliczyć za pomocą następującego wzoru:

P(X=k) = λ ^k * e ^{– λ} / k!

Złoto:

• λ: średnia liczba sukcesów występujących w określonym przedziale czasu
• k: liczba sukcesów
• e: stała równa około 2,71828

Załóżmy na przykład, że w konkretnym szpitalu odbywają się średnio 2 porody na godzinę. Możemy użyć powyższego wzoru, aby określić prawdopodobieństwo przeżycia 0, 1, 2, 3 narodzin itp. w danej godzinie:

• P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0,1353
• P(X=1) = 2 ¹ * e ^{– 2} / 1! = 0,2707
• P(X=2) = 2 ² * e ^{– 2} / 2! = 0,2707
• P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

Obejrzyj PMF

Często wizualizujemy funkcje masy prawdopodobieństwa za pomocą wykresów słupkowych.

Na przykład poniższy wykres słupkowy przedstawia prawdopodobieństwa związane z liczbą urodzeń na godzinę dla rozkładu Poissona opisanego w poprzednim przykładzie:

Należy pamiętać, że liczba urodzeń może sięgać nieskończoności, ale prawdopodobieństwa stają się tak małe po 10, że nie można ich nawet zobaczyć na wykresie słupkowym.

Właściwości PMF

Funkcja masy prawdopodobieństwa ma następujące właściwości:

1. Wszystkie prawdopodobieństwa są dodatnie. Na przykład prawdopodobieństwo, że na kostce wypadnie od 1 do 6, jest dodatnie, podczas gdy prawdopodobieństwo wszystkich pozostałych wyników wynosi zero.

2. Prawdopodobieństwo wszystkich wyników mieści się w przedziale od 0 do 1. Na przykład prawdopodobieństwo, że na kostce wypadnie od 1 do 6, wynosi 1/6, czyli 0,1666666 dla każdego wyniku.

3. Suma wszystkich prawdopodobieństw musi wynosić 1. Przykładowo suma prawdopodobieństw wyrzucenia kości na określoną liczbę wynosi 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1. /6 = 1.

Dodatkowe zasoby

Co to są zmienne losowe?
CDF lub PDF: jaka jest różnica?
Wprowadzenie do rozkładu dwumianowego
Wprowadzenie do rozkładu Poissona