Jak wykonać regresję hierarchiczną w stata

Regresja hierarchiczna to technika, którą możemy zastosować do porównania kilku różnych modeli liniowych.

Podstawową ideą jest to, że najpierw dopasowujemy model regresji liniowej do jednej zmiennej objaśniającej. Następnie dopasowujemy inny model regresji, korzystając z dodatkowej zmiennej objaśniającej. Jeśli współczynnik R-kwadrat (proporcja wariancji zmiennej odpowiedzi, którą można wyjaśnić zmiennymi objaśniającymi) w drugim modelu jest znacznie wyższy niż współczynnik R-kwadrat w poprzednim modelu, oznacza to, że drugi model jest lepszy.

Następnie powtarzamy proces dopasowywania dodatkowych modeli regresji z większą liczbą zmiennych objaśniających i sprawdzamy, czy nowsze modele oferują poprawę w porównaniu z poprzednimi modelami.

W tym samouczku przedstawiono przykład sposobu wykonywania regresji hierarchicznej w Stata.

Przykład: regresja hierarchiczna w Stata

Użyjemy wbudowanego zbioru danych o nazwie auto , aby zilustrować, jak przeprowadzić regresję hierarchiczną w Stata. Najpierw załaduj zestaw danych, wpisując w polu poleceń:

automatyczne korzystanie z systemu

Szybkie podsumowanie danych możemy uzyskać za pomocą następującego polecenia:

podsumować

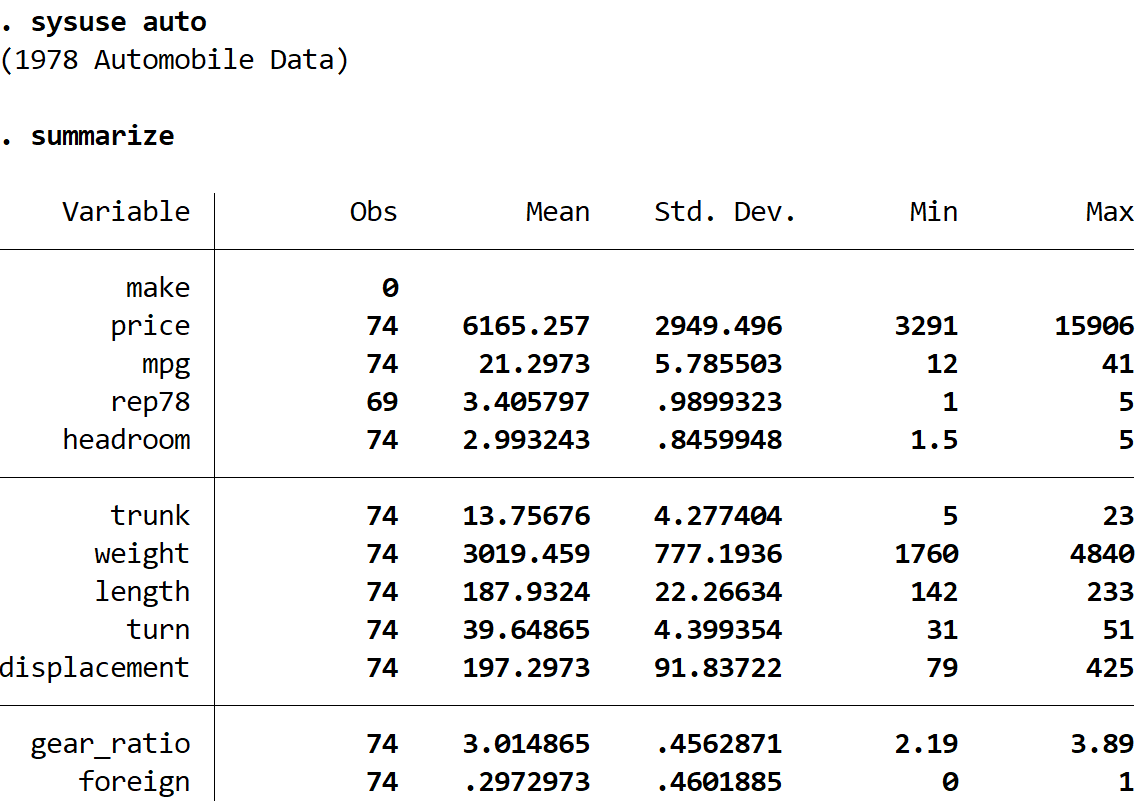
Widzimy, że zbiór danych zawiera informacje o 12 różnych zmiennych dla łącznie 74 samochodów.

Dopasujemy następujące trzy modele regresji liniowej i zastosujemy regresję hierarchiczną, aby sprawdzić, czy każdy kolejny model zapewnia znaczną poprawę w stosunku do poprzedniego:

Model 1: cena = przechwytywanie + mpg

Model 2: cena = przechwytywanie + mpg + waga

Model 3: cena = przechwytywanie + mpg + masa + przełożenie skrzyni biegów

Aby wykonać regresję hierarchiczną w Stacie, będziemy musieli najpierw zainstalować pakiet Hireg . Aby to zrobić, wpisz następujące polecenie w polu Polecenie:

znajdź Hirega

W wyświetlonym oknie kliknij Hireg z https://fmwww.bc.edu/RePEc/bocode/h

W następnym oknie kliknij łącze kliknij tutaj, aby zainstalować .

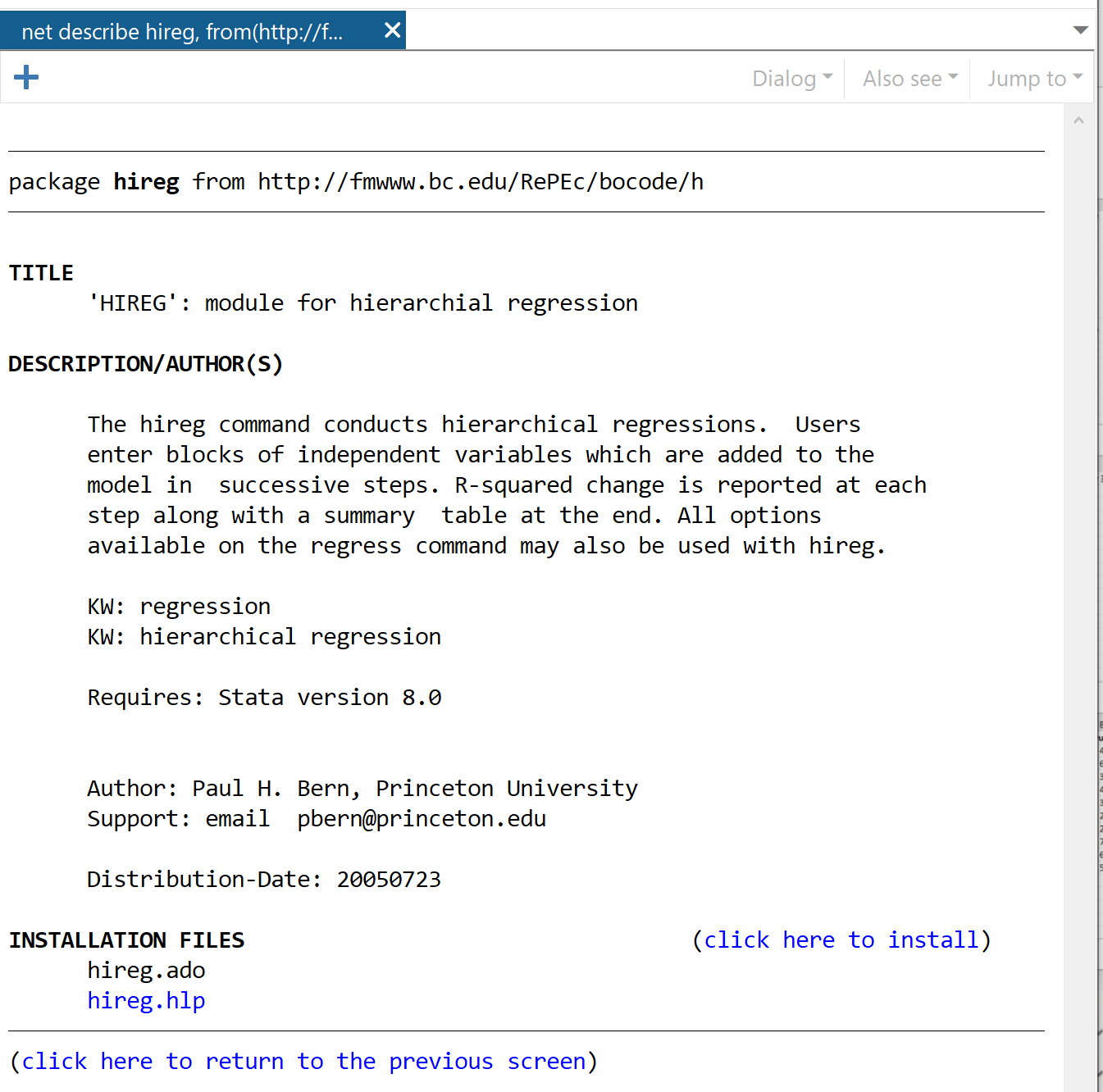
Pakiet zostanie zainstalowany w ciągu kilku sekund. Następnie, aby wykonać regresję hierarchiczną, użyjemy następującego polecenia:

cena wynajmu (mpg) (waga) (gear_ratio)

Oto, o co prosi Statę:

• Wykonaj regresję hierarchiczną, używając ceny jako zmiennej odpowiedzi w każdym modelu.
• W przypadku pierwszego modelu użyj mpg jako zmiennej objaśniającej.
• W przypadku drugiego modelu dodaj wagę jako dodatkową zmienną objaśniającą.
• W przypadku trzeciego modelu dodaj gear_ratio jako kolejną zmienną objaśniającą.

Oto wynik pierwszego modelu:

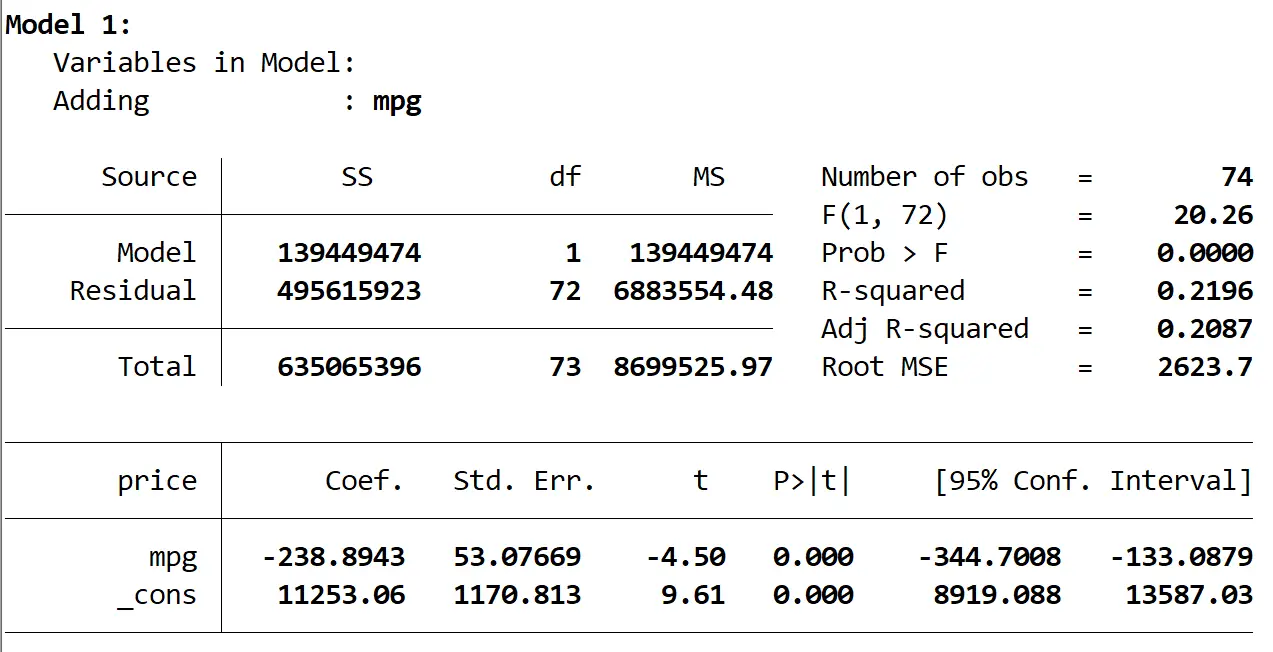
Widzimy, że R-kwadrat modelu wynosi 0,2196 , a ogólna wartość p (Prob > F) modelu wynosi 0,0000 , co jest statystycznie istotne przy α = 0,05.

Następnie widzimy wynik drugiego modelu:

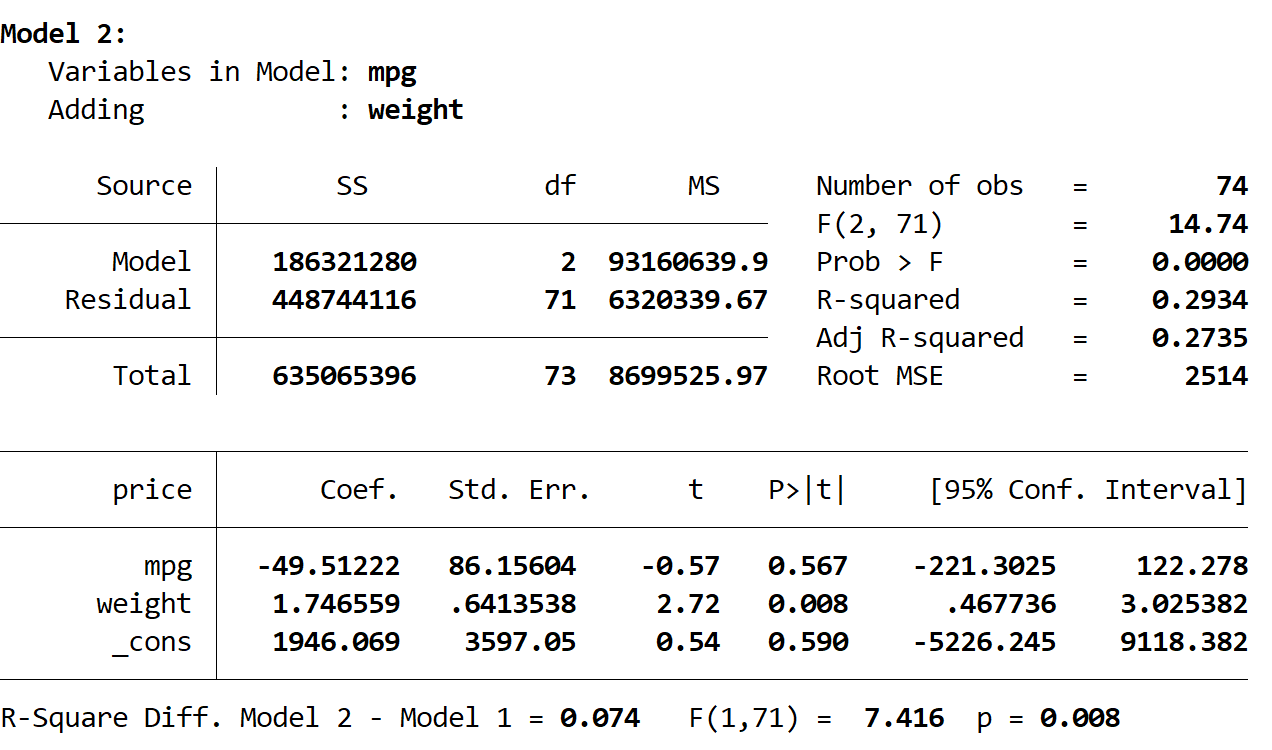
Kwadrat R tego modelu wynosi 0,2934 i jest większy niż w pierwszym modelu. Aby określić, czy ta różnica jest istotna statystycznie, Stata przeprowadziła test F, który na dole wyniku dał następujące liczby:

• R kwadrat różnicy między dwoma modelami = 0,074
• Statystyka F dla różnicy = 7,416
• Odpowiednia wartość p statystyki F = 0,008

Ponieważ wartość p jest mniejsza niż 0,05, dochodzimy do wniosku, że w drugim modelu nastąpiła statystycznie istotna poprawa w porównaniu z pierwszym modelem.

Wreszcie możemy zobaczyć wynik trzeciego modelu:

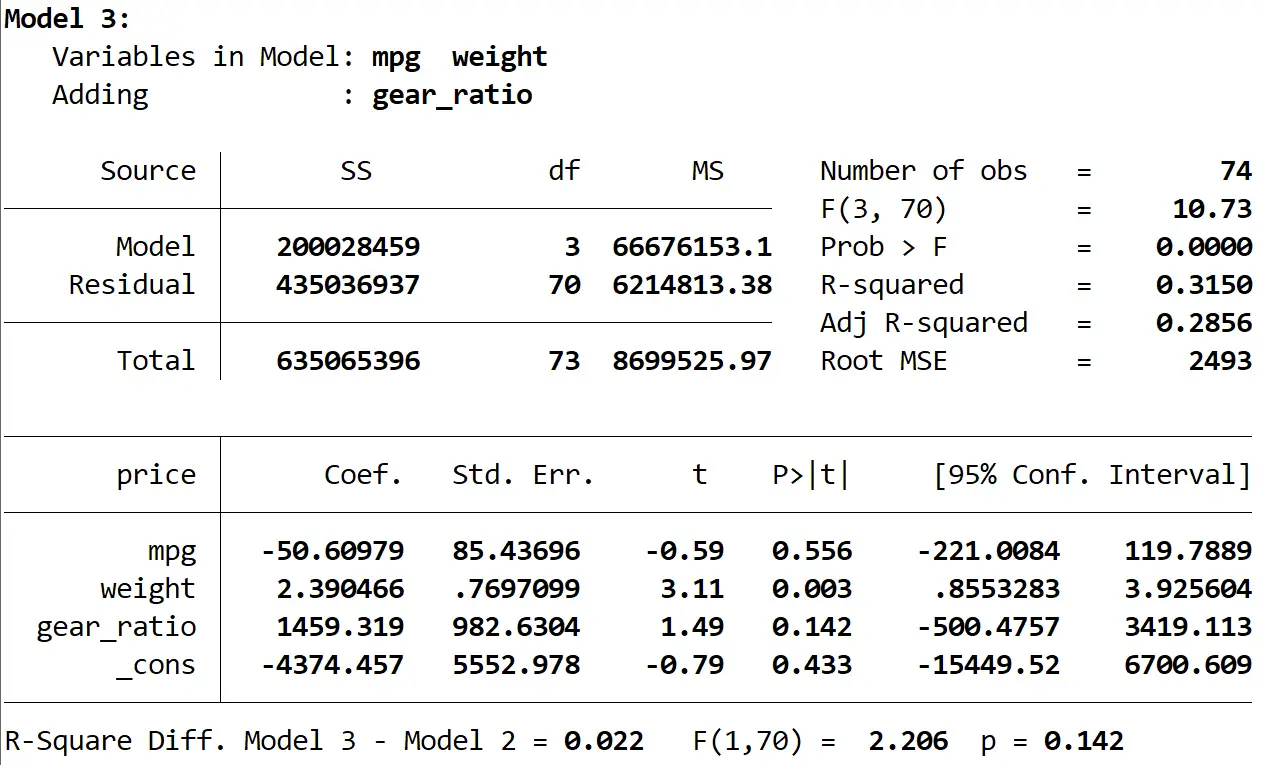
Kwadrat R tego modelu wynosi 0,3150 i jest większy niż kwadrat R w drugim modelu. Aby określić, czy ta różnica jest istotna statystycznie, Stata przeprowadziła test F, który na dole wyniku dał następujące liczby:

• R kwadrat różnicy między dwoma modelami = 0,022
• Statystyka F dla różnicy = 2,206
• Odpowiednia wartość p statystyki F = 0,142

Ponieważ wartość p jest nie mniejsza niż 0,05, nie mamy wystarczających dowodów, aby stwierdzić, że trzeci model zapewnia poprawę w porównaniu z drugim modelem.

Już na samym końcu wyniku widzimy, że Stata podaje podsumowanie wyników:

W tym konkretnym przykładzie doszlibyśmy do wniosku, że Model 2 zapewniał znaczną poprawę w porównaniu z Modelem 1, ale Model 3 nie zapewniał znaczącej poprawy w porównaniu z Modelem 2.