Jak wykonać test kruskala-wallisa w stata
Test Kruskala-Wallisa służy do określenia, czy istnieje statystycznie istotna różnica między medianami trzech lub więcej niezależnych grup. Uważa się, że jest to nieparametryczny odpowiednik jednokierunkowej analizy wariancji ANOVA .
W tym samouczku wyjaśniono, jak wykonać test Kruskala-Wallisa w Stata.
Jak wykonać test Kruskala-Wallisa w Stata
W tym przykładzie użyjemy zbioru danych Census , który zawiera dane ze spisu powszechnego z 1980 roku dla wszystkich pięćdziesięciu stanów w Stanach Zjednoczonych. W zbiorze danych stany są podzielone na cztery różne regiony:
- Nord Est
- Północno-centralna
- Południe
- Zachód
Przeprowadzimy test Kruskala-Wallisa, aby ustalić, czy mediana wieku jest równa w tych czterech regionach.
Krok 1: Załaduj i wyświetl dane.
Najpierw załaduj zestaw danych, wpisując następujące polecenie w polu Polecenie:
użyj https://www.stata-press.com/data/r13/census
Uzyskaj szybkie podsumowanie zbioru danych za pomocą następującego polecenia:
podsumować
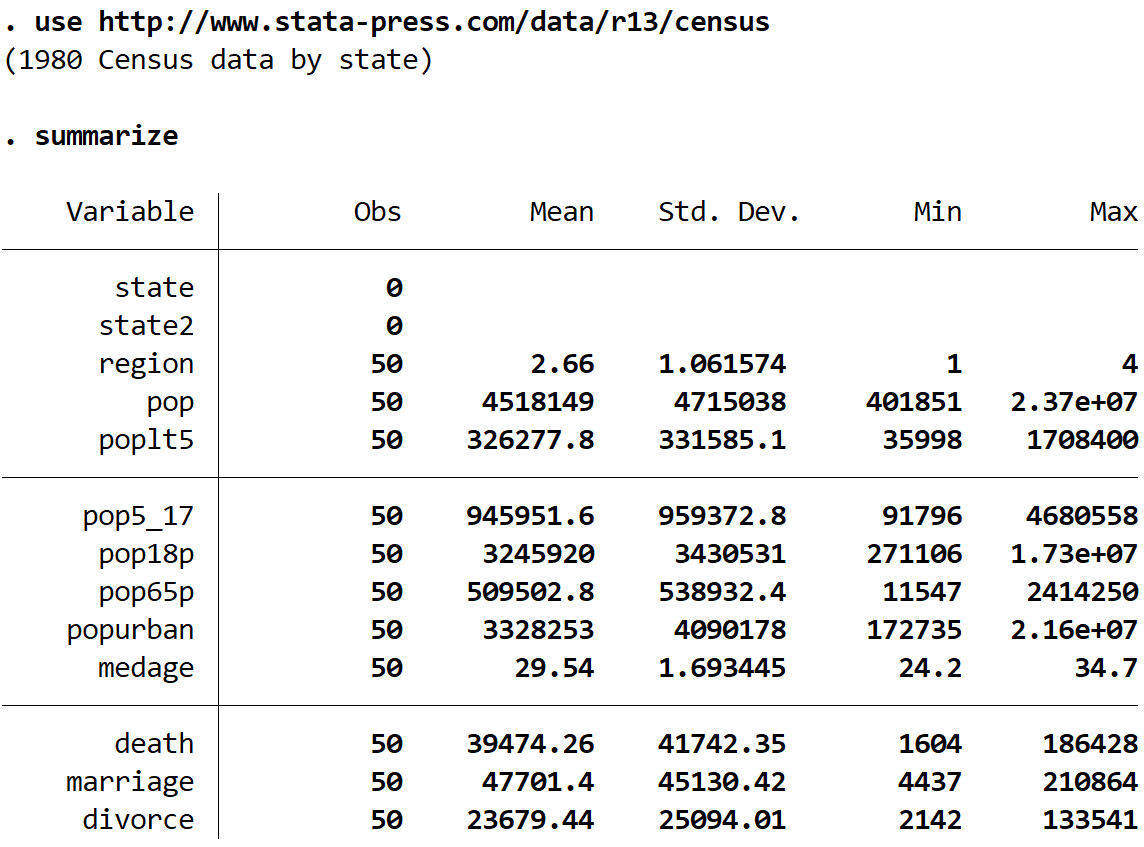
Widzimy, że w tym zbiorze danych znajduje się 13 różnych zmiennych, ale będziemy pracować tylko z dwoma : średni wiek (mediana wieku) i region .
Krok 2: Wizualizuj dane.
Przed wykonaniem testu Kruskala-Wallisa utwórzmy najpierw kilka wykresów pudełkowych , aby zwizualizować rozkład mediany wieku dla każdego z czterech regionów:
pole graficzne wiadomości, włączone (region)
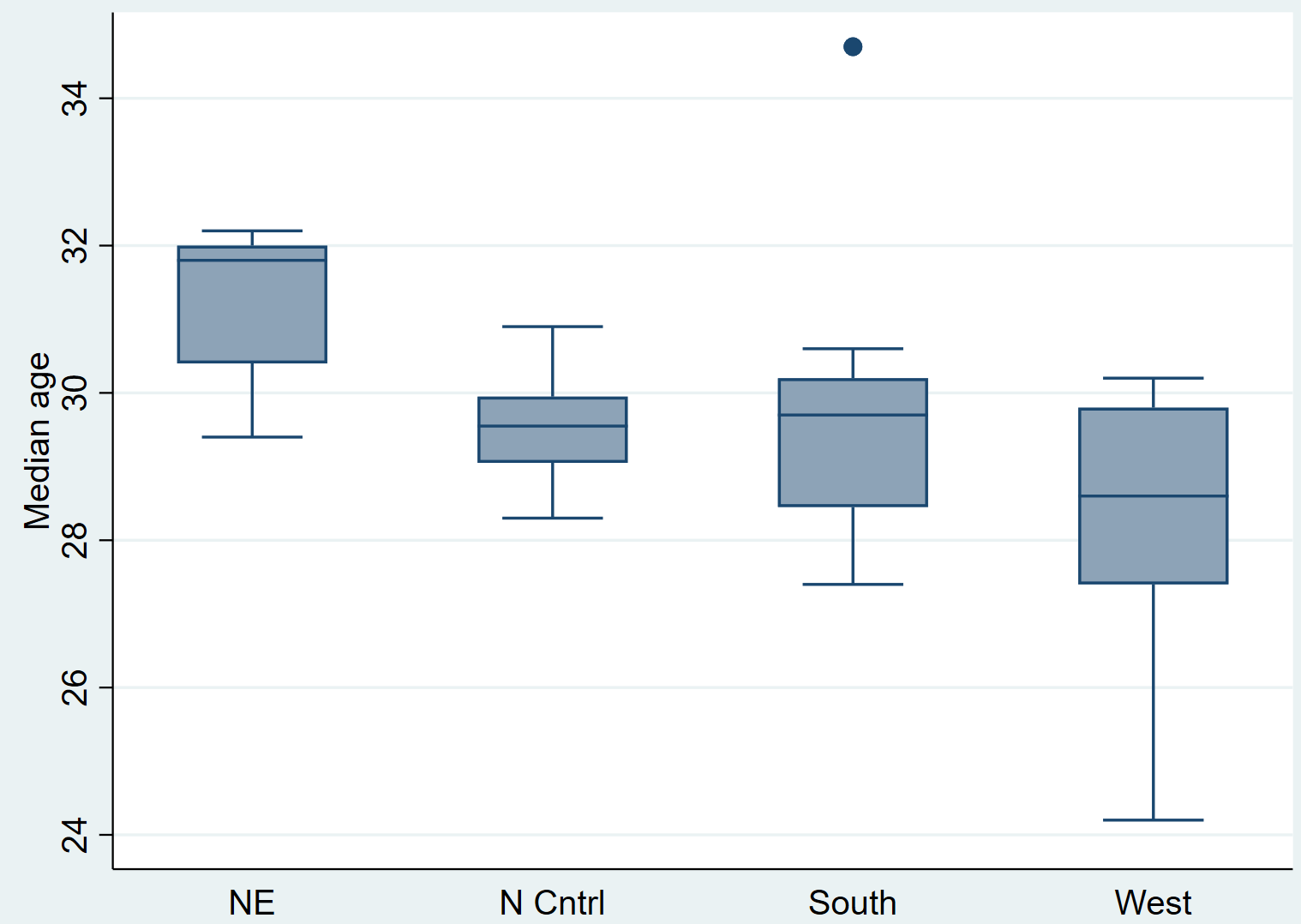
Wystarczy spojrzeć na wykresy pudełkowe, aby zobaczyć, że rozkłady wydają się różnić w zależności od regionu. Następnie przeprowadzimy test Kruskala-Wallisa, aby sprawdzić, czy różnice te są istotne statystycznie.
Krok 3: Wykonaj test Kruskala-Wallisa.
Aby wykonać test Kruskala-Wallisa, użyj poniższej składni:
kwallis zmienna_miary, według (zmienna_grupowania)
W naszym przypadku zastosujemy następującą składnię:
kwallis medage, według (regionu)
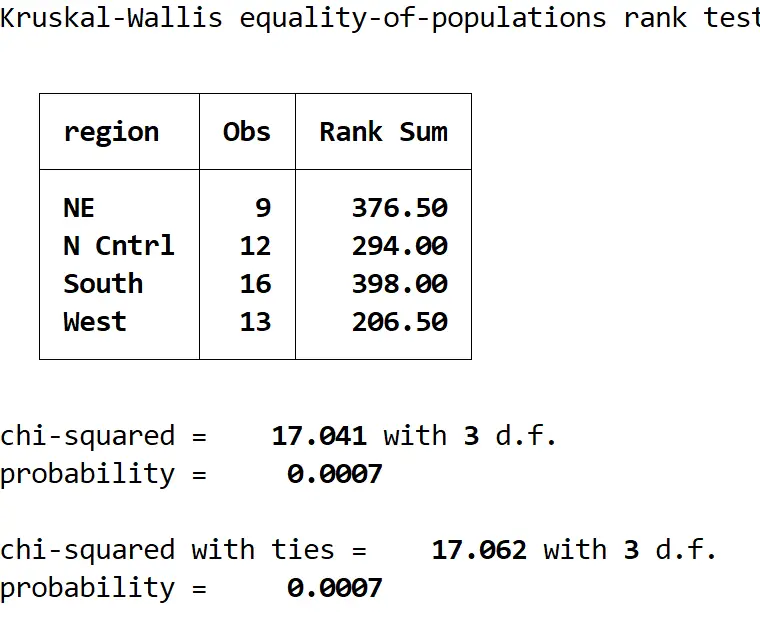
Oto jak zinterpretować wynik:
Tabela podsumowująca: Ta tabela pokazuje liczbę obserwacji na region i sumy rankingowe dla każdego regionu.
Chi-kwadrat z remisami: Jest to wartość statystyki testowej, która wynosi 17,062.
prawdopodobieństwo: Jest to wartość p odpowiadająca statystyce testowej, która okazuje się wynosić 0,0007. Ponieważ wartość ta jest mniejsza niż 0,05, możemy odrzucić hipotezę zerową i stwierdzić, że mediana wieku nie jest równa w czterech regionach.
Krok 4: Ogłoś wyniki.
Na koniec chcielibyśmy przedstawić wyniki testu Kruskala-Wallisa. Oto przykład, jak to zrobić:
Przeprowadzono test Kruskala-Wallista w celu ustalenia, czy mediana wieku osób była taka sama w następujących czterech regionach Stanów Zjednoczonych:
- Północno-wschodni (n=9)
- Północno-Środkowy (n=12)
- Południe (n=16)
- Zachód (n=13)
Test wykazał, że mediana wieku osób nie była jednakowa w czterech regionach (X 2 = 17,062, p = 0,0007). Oznacza to, że istniała statystycznie istotna różnica w medianie wieku między dwoma lub większą liczbą regionów.