Stdev.p vs stdev.s w excelu: jaka jest różnica?

Istnieją trzy różne funkcje, których można użyć do obliczenia odchylenia standardowego w programie Excel:

1. STDEV.P: Ta funkcja oblicza odchylenie standardowe populacji. Użyj tej funkcji, gdy zakres wartości reprezentuje całą populację.

Ta funkcja wykorzystuje następującą formułę:

Odchylenie standardowe populacji = √Σ (x _i – μ) ² / N

Złoto:

• Σ: grecki symbol oznaczający „sumę”
• x _i : ^i-ta wartość zbioru danych
• μ: średnia populacji
• N: Całkowita liczba obserwacji

2. STDEV.S: Ta funkcja oblicza odchylenie standardowe próbki. Użyj tej funkcji, gdy zakres wartości reprezentuje próbkę wartości, a nie całą populację.

Ta funkcja wykorzystuje następującą formułę:

Odchylenie standardowe próbki = √Σ (x _i – x ) ² / (n-1)

Złoto:

• Σ: grecki symbol oznaczający „sumę”
• x _i : ^i-ta wartość zbioru danych
• x : Przykładowe środki
• N: Całkowita liczba obserwacji

3. STDEV: Ta funkcja oblicza również odchylenie standardowe próbki. Zwróci dokładnie tę samą wartość, co funkcja STDEV.S .

Uwaga techniczna:

Ponieważ wzór na odchylenie standardowe populacji jest dzielony przez N zamiast n-1 , odchylenie standardowe populacji będzie zawsze mniejsze niż odchylenie standardowe próbki.

Powodem, dla którego odchylenie standardowe populacji będzie mniejsze, jest to, że jeśli znamy każdą wartość populacji, to znamy dokładne odchylenie standardowe.

Jednakże, gdy mamy tylko próbkę populacji, mamy większą niepewność co do dokładnego odchylenia standardowego całej populacji, więc nasze oszacowanie odchylenia standardowego musi być większe.

Poniższy przykład pokazuje, jak w praktyce wykorzystać te funkcje.

Przykład: STDEV.P vs STDEV.S w Excelu

Załóżmy, że w Excelu mamy następujący zestaw danych:

Poniższy zrzut ekranu pokazuje, jak obliczyć odchylenie standardowe zbioru danych przy użyciu trzech różnych wzorów na odchylenie standardowe:

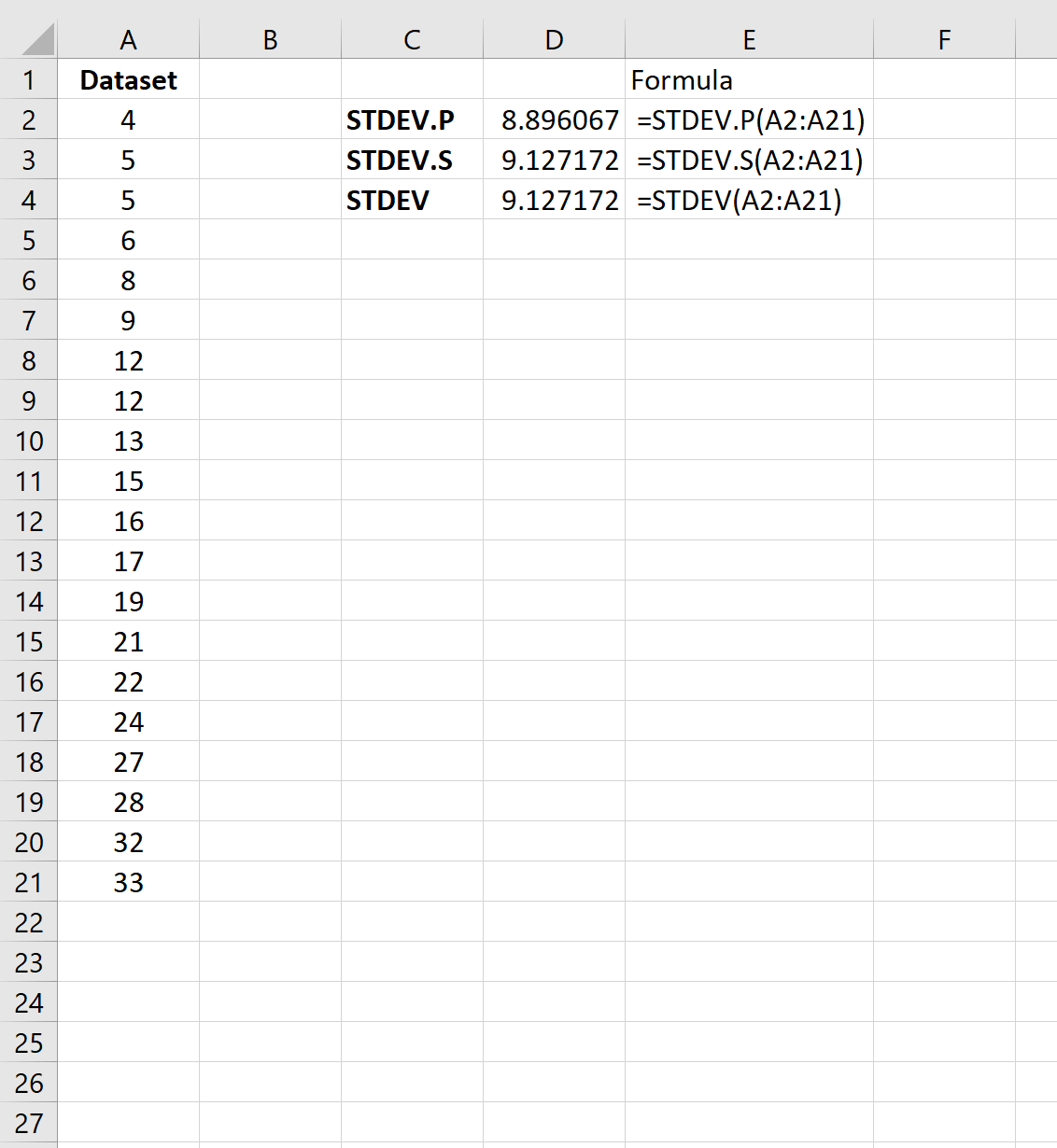
Odchylenie standardowe próbki wynosi 9,127 , a odchylenie standardowe populacji wynosi 8,896 .

Jak wspomniano wcześniej, odchylenie standardowe populacji będzie zawsze mniejsze niż odchylenie standardowe próbki.

Kiedy używać STDEV.P vs. STDEV.S

W większości przypadków nie jesteśmy w stanie zebrać danych dla całej populacji. Dlatego zbieramy dane tylko dla próbki populacji.

Dlatego prawie zawsze używamy STDEV.S do obliczenia odchylenia standardowego zbioru danych, ponieważ nasz zbiór danych zazwyczaj reprezentuje próbkę.

Należy zauważyć, że STDEV i STDEV.S zwracają dokładnie te same wartości, więc możemy użyć dowolnej funkcji do obliczenia odchylenia standardowego próbki dla danego zbioru danych.