Błąd berksona: definicja + przykłady

Błąd Berksona to rodzaj błędu systematycznego, który pojawia się w badaniach, gdy dwie zmienne wydają się być ujemnie skorelowane w danych próbki, ale w rzeczywistości są dodatnio skorelowane w całej populacji .

Załóżmy na przykład, że Tomek chce zbadać korelację między jakością hamburgerów i koktajli mlecznych w lokalnych restauracjach.

Wychodzi i zbiera następujące dane na temat siedmiu różnych restauracji:

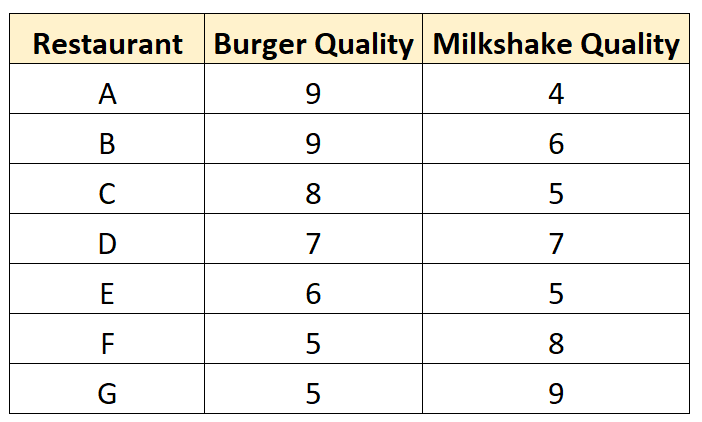
Tworzy wykres punktowy do wizualizacji danych:

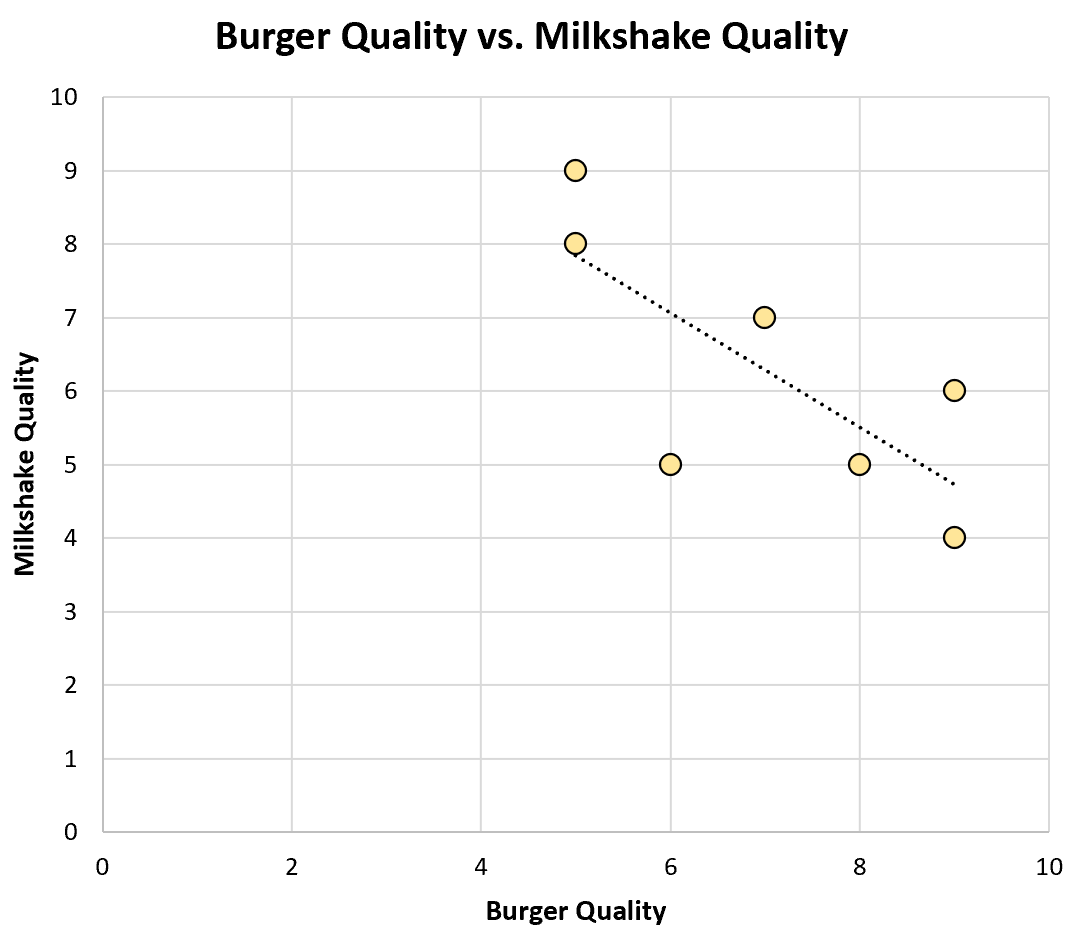
Współczynnik korelacji Pearsona pomiędzy tymi dwiema zmiennymi wynosi -0,75 , co odpowiada silnej korelacji ujemnej.

To odkrycie jest dla Toma sprzeczne z intuicją: pomyślałby, że restauracje, które robią dobre hamburgery, robią też dobre koktajle mleczne.

Okazuje się jednak, że Tom po prostu zignorował wszystkie restauracje w mieście, które robią zarówno kiepskie burgery , jak i kiepskie koktajle mleczne.

Gdyby odwiedził te restauracje, zebrałby następujący zestaw danych:

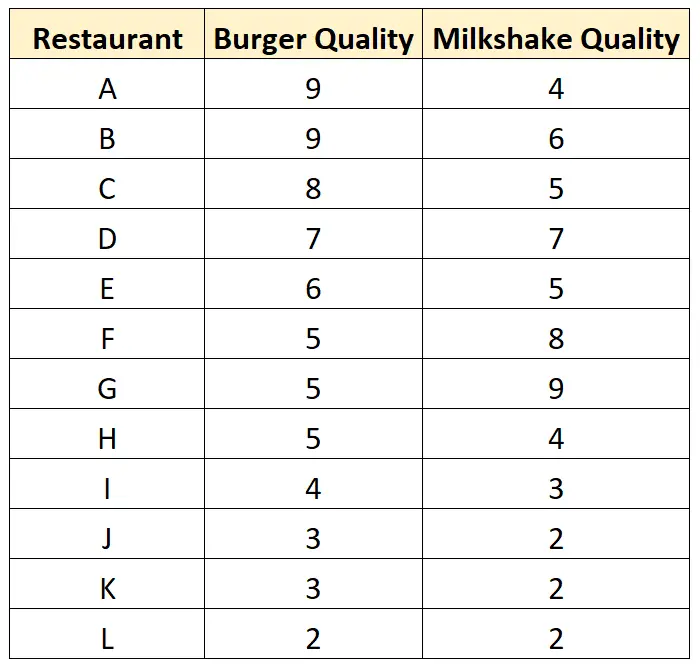
A tak wygląda wykres rozrzutu dla tego zbioru danych:

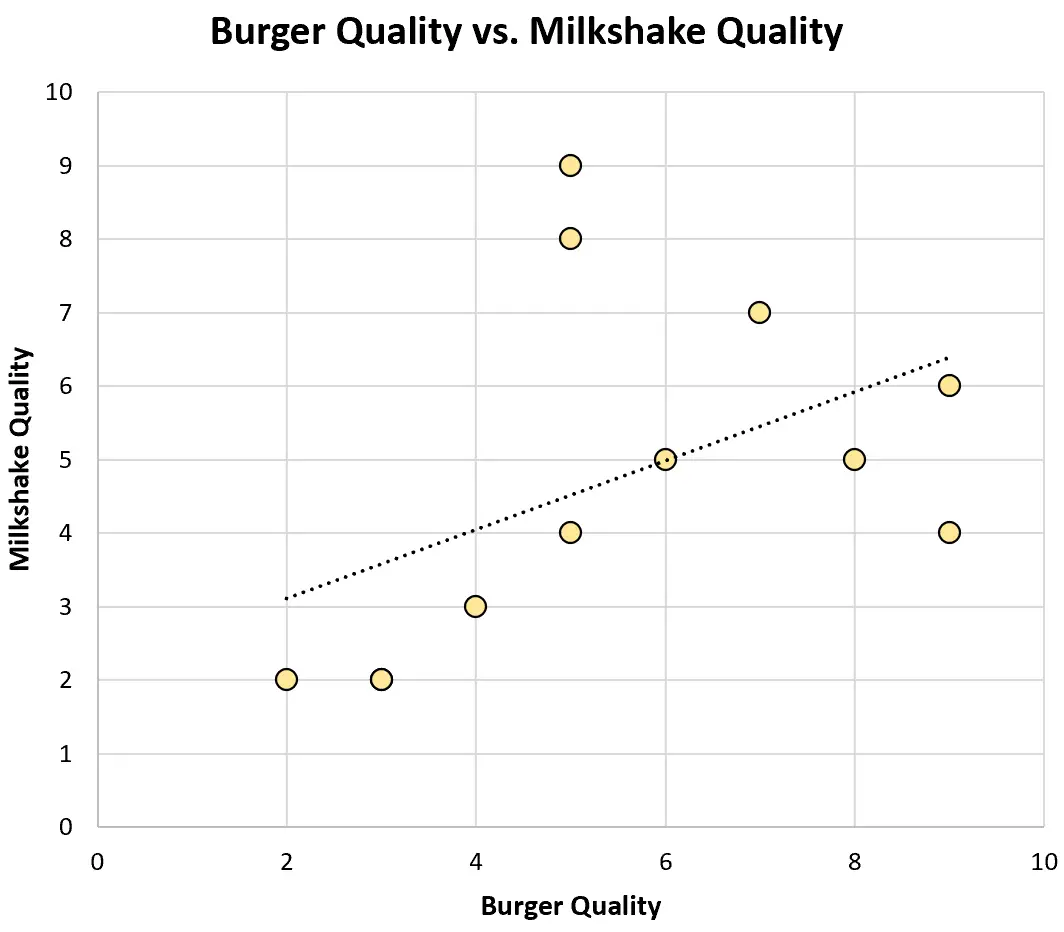
Współczynnik korelacji Pearsona pomiędzy obiema zmiennymi okazuje się wynosić 0,46 , co oznacza umiarkowanie silną dodatnią korelację.

Badając jedynie podzbiór restauracji w mieście, Tom błędnie doszedł do wniosku, że istnieje ujemna korelacja między jakością burgerów i koktajli mlecznych.

Okazuje się bowiem, że pomiędzy tymi dwiema zmiennymi istnieje dodatnia zależność (jak można się było spodziewać). To klasyczny przykład stronniczości Berksona.

Zobacz poniższe przykłady innych scenariuszy, w których w praktyce występuje stronniczość Berksona.

Przykład 1: Rekrutacja na studia

Załóżmy, że uczelnia przyjmuje tylko studentów, którzy mają wystarczająco wysoki wynik GPA i ACT.

Powszechnie wiadomo, że te dwie zmienne są ze sobą dodatnio skorelowane, okazuje się jednak, że wśród studentów decydujących się na naukę w danej uczelni wydaje się, że istnieje między nimi ujemna korelacja.

Jednak ta ujemna korelacja występuje tylko dlatego, że studenci, którzy mają zarówno wysoki wynik GPA, jak i ACT, mogą studiować na elitarnym uniwersytecie, podczas gdy studenci, którzy mają zarówno niski wynik GPA, jak i ACT, nie są w ogóle przyjmowani.

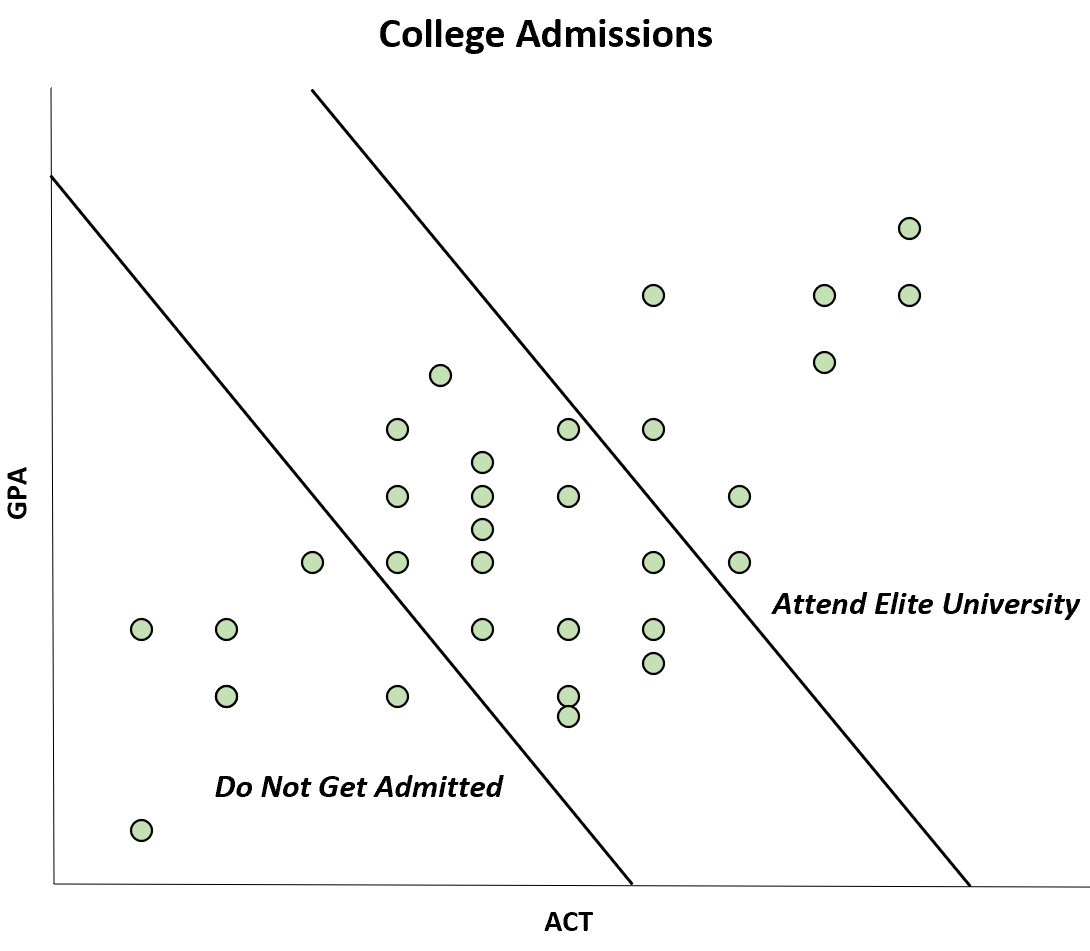
Chociaż korelacja między ACT i GPA jest w populacji dodatnia, w próbie korelacja wydaje się ujemna. Jest to przypadek stronniczości ze strony Berksona.

Przykład 2: Preferencje randkowe

Wiele osób umawia się tylko z partnerami, którzy są atrakcyjni i mają dobrą osobowość.

W prawdziwym świecie może nie być korelacji między tymi dwiema zmiennymi, ale zawężając grupę randkową, dana osoba może całkowicie zignorować potencjalnych partnerów, którzy są zarówno nieatrakcyjni, jak i utalentowani. „dobra osobowość”.

Zatem wśród potencjalnych partnerów może się wydawać, że istnieje ujemna korelacja pomiędzy tymi dwiema zmiennymi: osoby bardziej atrakcyjne mają gorszą osobowość, a osoby o lepszej osobowości wydają się mniej atrakcyjne.

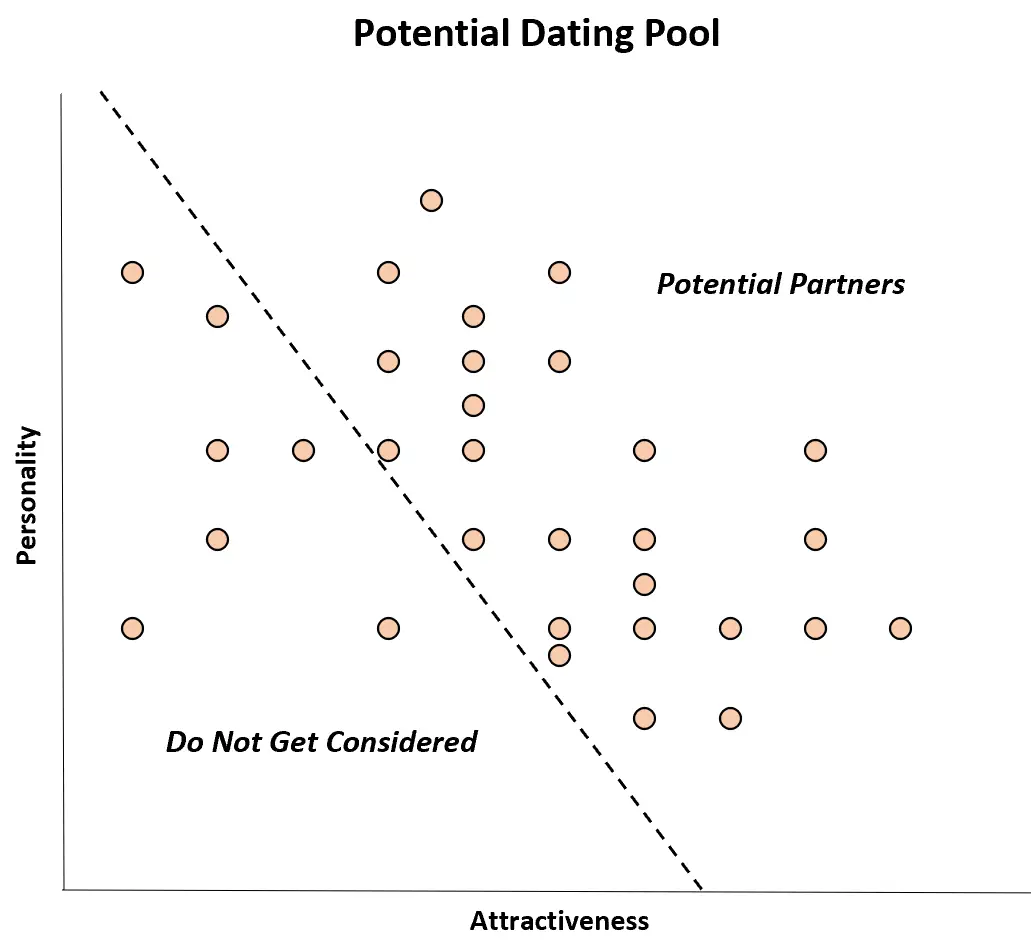
Chociaż w populacji nie ma korelacji między tymi dwiema zmiennymi, wydaje się, że w próbie potencjalnych partnerów występuje korelacja ujemna. Jest to po prostu przypadek stronniczości Berksona.

Jak zapobiegać stronniczości Berksona

Najbardziej oczywistym sposobem uniknięcia stronniczości Berksona w badaniach naukowych jest pobranie prostej losowej próbki z populacji. Innymi słowy, upewnij się, że każdy członek populacji będącej przedmiotem zainteresowania ma równe szanse na włączenie do próby.

Na przykład, jeśli badasz częstość występowania chorób w danym kraju, musisz zebrać próbę osób z całego kraju, a nie tylko tych, do których łatwo dotrzeć w szpitalach.

Korzystając z prostej próby losowej, badacze mogą zmaksymalizować szansę, że wybrana przez nich próba będzie reprezentatywna dla populacji, co oznacza, że będą mogli z całą pewnością uogólnić swoje ustalenia z próbki na całą populację.