Jak wykonać test t dla nierównej wielkości próbek

Pytanie, które uczniowie często zadają, jeśli chodzi o statystyki, brzmi:

Czy można przeprowadzić test t, gdy liczebność prób w każdej grupie nie jest równa?

Krótka odpowiedź:

Tak, można wykonać test t, gdy liczebność próbek nie jest równa. Równe wielkości próbek nie są jednym z założeń przyjętych w teście t.

Prawdziwe problemy pojawiają się, gdy dwie próbki nie mają równych wariancji, co jest jednym z założeń przyjętych w teście t.

W takim przypadku zaleca się zamiast tego użycie testu t Welcha , który nie zakłada równych wariancji.

Poniższe przykłady pokazują, jak przeprowadzić testy T dla próbek o różnej wielkości, gdy wariancje są równe i gdy nie są.

Przykład 1: Nierówne wielkości próbek i równe wariancje

Załóżmy, że administrujemy dwoma programami, które mają pomóc uczniom osiągać lepsze wyniki na niektórych egzaminach.

Wyniki są następujące:

Program 1:

• n (wielkość próbki): 500
• x (średnia próbki): 80
• s (przykładowe odchylenie standardowe): 5

Program 2:

• n (wielkość próbki): 20
• x (średnia próbki): 85
• s (przykładowe odchylenie standardowe): 5

Poniższy kod pokazuje, jak utworzyć wykres pudełkowy w języku R, aby zwizualizować rozkład wyników egzaminów dla każdego programu:

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=5)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

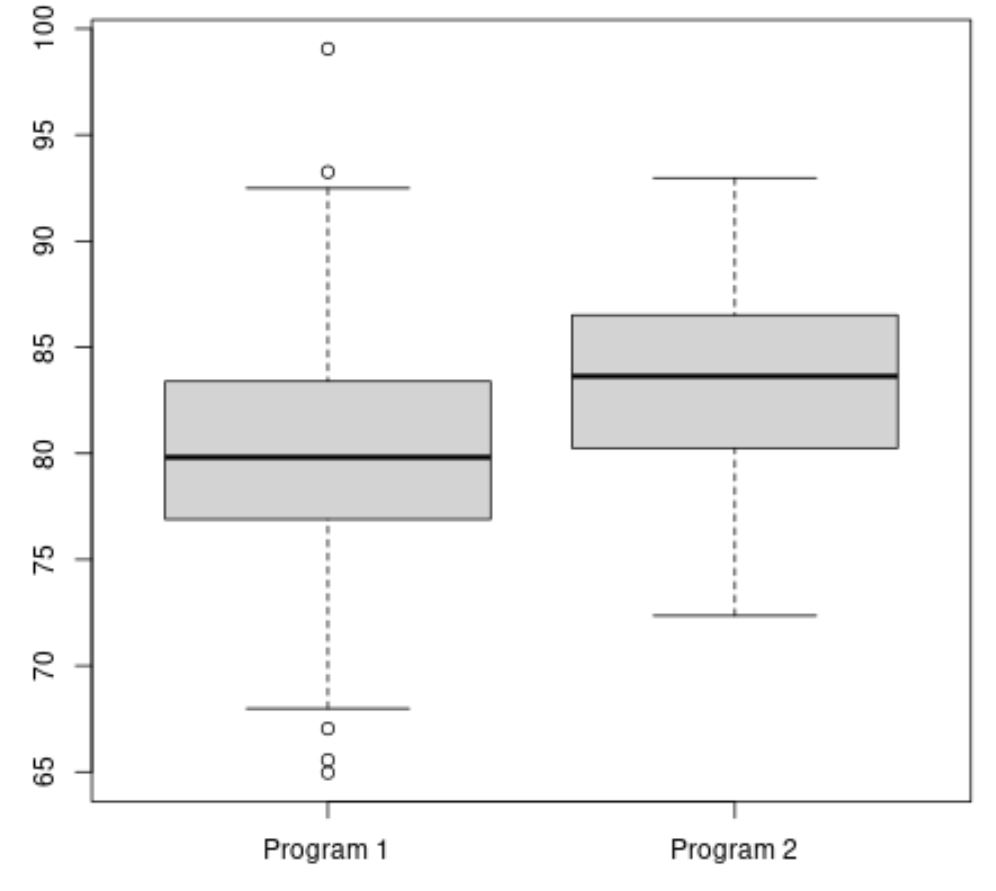
Średni wynik egzaminu w ramach Programu 2 wydaje się wyższy, ale różnice w wynikach egzaminów pomiędzy obydwoma programami są w przybliżeniu równe.

Poniższy kod pokazuje, jak przeprowadzić test t dla niezależnych próbek za pomocą testu t Welcha:

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -3.3348, df = 518, p-value = 0.0009148
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.111504 -1.580245
sample estimates:
mean of x mean of y 
 80.11322 83.95910

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -3.3735, df = 20.589, p-value = 0.00293
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.219551 -1.472199
sample estimates:
mean of x mean of y 
 80.11322 83.95910 

Test t niezależnych próbek zwraca wartość p 0,0009 , a test t Welcha zwraca wartość p 0,0029 .

Ponieważ wartość p każdego testu jest mniejsza niż 0,05, odrzucilibyśmy hipotezę zerową w każdym teście i doszliśmy do wniosku, że istnieje statystycznie istotna różnica w średnich wynikach egzaminów pomiędzy obydwoma programami.

Mimo że rozmiary próbek są nierówne, test t dla niezależnych próbek i test t Welcha dają podobne wyniki, ponieważ obie próbki miały równe wariancje.

Przykład 2: Nierówne wielkości próbek i nierówne wariancje

Załóżmy, że administrujemy dwoma programami, które mają pomóc uczniom osiągać lepsze wyniki na niektórych egzaminach.

Wyniki są następujące:

Program 1:

• n (wielkość próbki): 500
• x (średnia próbki): 80
• s (przykładowe odchylenie standardowe): 25

Program 2:

• n (wielkość próbki): 20
• x (średnia próbki): 85
• s (przykładowe odchylenie standardowe): 5

Poniższy kod pokazuje, jak utworzyć wykres pudełkowy w języku R, aby zwizualizować rozkład wyników egzaminów dla każdego programu:

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=25)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

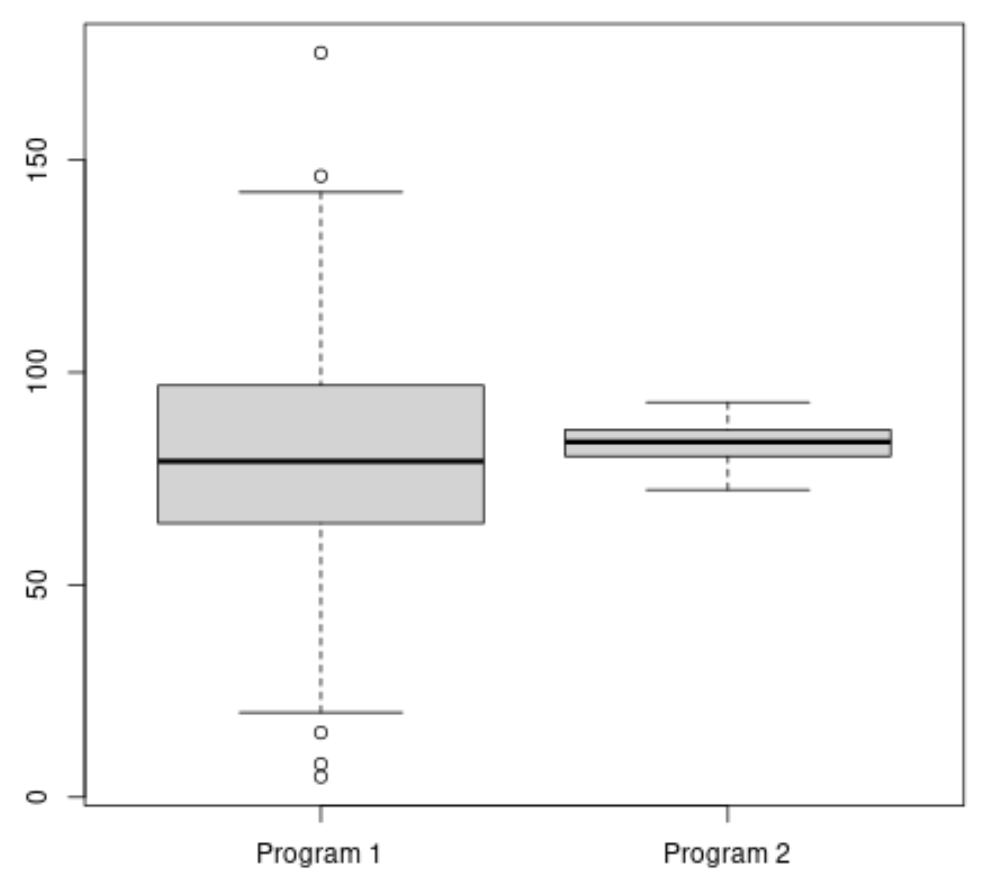
Średni wynik egzaminu dla Programu 2 wydaje się wyższy, ale rozbieżność wyników egzaminu dla Programu 1 jest znacznie większa niż w przypadku Programu 2.

Poniższy kod pokazuje, jak przeprowadzić test t dla niezależnych próbek za pomocą testu t Welcha:

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -0.5988, df = 518, p-value = 0.5496
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -14.52474 7.73875
sample estimates:
mean of x mean of y 
  80.5661 83.9591

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -2.1338, df = 74.934, p-value = 0.03613
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.560690 -0.225296
sample estimates:
mean of x mean of y 
  80.5661 83.9591 

Test t niezależnych próbek zwraca wartość p 0,5496 , a test t Welcha zwraca wartość p 0,0361 .

Test t niezależnych próbek nie jest w stanie wykryć różnicy w średnich wynikach egzaminu, ale test t Welcha jest w stanie wykryć różnicę istotną statystycznie.

Ponieważ obie próbki miały nierówne wariancje, jedynie test t Welcha był w stanie wykryć statystycznie istotną różnicę w średnich wynikach egzaminu, ponieważ test ten nie zakłada równych wariancji między próbami .

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat testów t:

Wprowadzenie do testu t dla jednej próby
Wprowadzenie do testu t dla dwóch prób
Wprowadzenie do testu t dla par próbek