Zrozumienie testu t w regresji liniowej

Regresję liniową stosuje się do ilościowego określenia związku między zmienną predykcyjną a zmienną odpowiedzi.

Ilekroć przeprowadzamy regresję liniową, chcemy wiedzieć, czy istnieje statystycznie istotna zależność pomiędzy zmienną predykcyjną a zmienną odpowiedzi.

Sprawdzamy istotność, wykonując test t dla nachylenia regresji. W tym teście t używamy następującej hipotezy zerowej i alternatywnej:

• H ₀ : β ₁ = 0 (nachylenie równe zeru)
• H _A : β ₁ ≠ 0 (nachylenie nie jest równe zero)

Następnie obliczamy statystykę testową w następujący sposób:

t = b / SE _b

Złoto:

• b : oszacowanie współczynnika
• SE _b : błąd standardowy oszacowania współczynnika

Jeśli wartość p odpowiadająca t jest poniżej pewnego progu (np. α = 0,05), wówczas odrzucamy hipotezę zerową i stwierdzamy, że istnieje statystycznie istotna zależność pomiędzy zmienną predykcyjną a zmienną odpowiedzi.

Poniższy przykład pokazuje, jak w praktyce przeprowadzić test t dla modelu regresji liniowej.

Przykład: Przeprowadzanie testu t dla regresji liniowej

Załóżmy, że profesor chce przeanalizować związek między przepracowanymi godzinami a ocenami z egzaminów dla 40 swoich studentów.

Wykonuje prostą regresję liniową, wykorzystując przestudiowane godziny jako zmienną predykcyjną i uzyskane wyniki egzaminów jako zmienną odpowiedzi.

Poniższa tabela przedstawia wyniki modelu regresji:

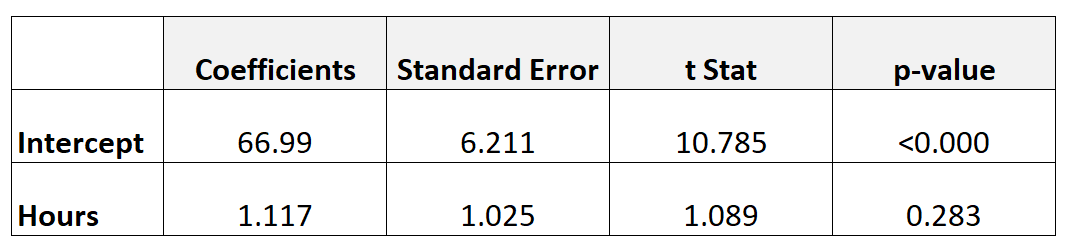
Aby ustalić, czy przepracowane godziny mają statystycznie istotny związek z oceną końcową z egzaminu, możemy wykonać test t.

W tym teście t używamy następującej hipotezy zerowej i alternatywnej:

• H ₀ : β ₁ = 0 (nachylenie badanych godzin jest równe zeru)
• H _A : β ₁ ≠ 0 (nachylenie badanych godzin nie jest równe zero)

Następnie obliczamy statystykę testową w następujący sposób:

• t = b / SE _b
• t = 1,117 / 1,025
• t = 1,089

Wartość p odpowiadająca t = 1,089 przy df = n-2 = 40 – 2 = 38 wynosi 0,283 .

Zauważ, że możemy również użyć kalkulatora wartości T do P, aby obliczyć tę wartość p:

Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej.

Oznacza to, że przestudiowane godziny nie mają istotnego statystycznie związku pomiędzy wynikami egzaminu końcowego.

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat regresji liniowej:

Wprowadzenie do prostej regresji liniowej
Wprowadzenie do wielokrotnej regresji liniowej
Jak interpretować współczynniki regresji
Jak interpretować test F dla ogólnej istotności w regresji