Test bartletta na jednorodność wariancji (definicja i przykład)

Test Bartletta jest testem statystycznym stosowanym do określenia, czy wariancje między wieloma grupami są równe.

Wiele testów statystycznych (takich jak jednoczynnikowa ANOVA ) zakłada, że wariancje są równe pomiędzy próbkami. Aby zweryfikować tę hipotezę, można zastosować test Bartletta.

Poniższe kroki wyjaśniają, jak przeprowadzić test Bartletta.

Uwaga: Nie należy mylić tego testu z testem sferyczności Bartletta , który służy do porównania obserwowanej macierzy korelacji z macierzą tożsamości.

Kroki wykonania testu Bartletta

Test Bartletta wykorzystuje następujące hipotezy zerowe i alternatywne:

H ₀ : Wariancja pomiędzy każdą grupą jest równa.

H _A : Co najmniej jedna grupa ma wariancję, która nie jest równa pozostałym.

Statystykę testową można obliczyć w następujący sposób:

B = (nk)lns ² – Σ(n _j -1)lns _j ² / c

Złoto:

• n: całkowita liczba obserwacji we wszystkich grupach
• k: Całkowita liczba grup
• ln: Oznacza to „log naturalny”
• s ² : Łączna wariancja
• n _j : Liczba obserwacji w grupie j
• s _j ² : Wariancja grupy j

A gdzie jest to obliczane w następujący sposób:

• c = 1 + (1/3(k-1))*(Σ(1/(n _j -1)) – (1/(nk))

Ta statystyka testowa ma rozkład Chi-kwadrat z k-1 stopniami swobody. Innymi słowy, B ~ X ² (k-1).

Jeśli wartość p odpowiadająca statystyce testowej jest poniżej pewnego poziomu istotności (np. α = 0,05), wówczas możemy odrzucić hipotezę zerową i stwierdzić, że nie wszystkie grupy mają tę samą wariancję.

Przykład: test Bartletta

Załóżmy, że profesor chce wiedzieć, czy trzy różne techniki uczenia się prowadzą do różnych średnich ocen na egzaminach.

Losowo przydziela 10 uczniów do stosowania każdej techniki przez tydzień, a następnie przydziela każdemu uczniowi egzamin o równym stopniu trudności.

Poniżej prezentujemy wyniki egzaminów 30 uczniów:

Profesor chce przeprowadzić jednoczynnikową analizę ANOVA, aby sprawdzić, czy te trzy techniki prowadzą do różnych średnich wyników na egzaminie, ale najpierw musi wykonać test Bartletta, aby sprawdzić, czy trzy grupy mają równe wariancje.

Ręczne wykonywanie testu Bartletta jest żmudne, dlatego do kalkulatora testu Bartletta wprowadzimy następujące wartości danych:

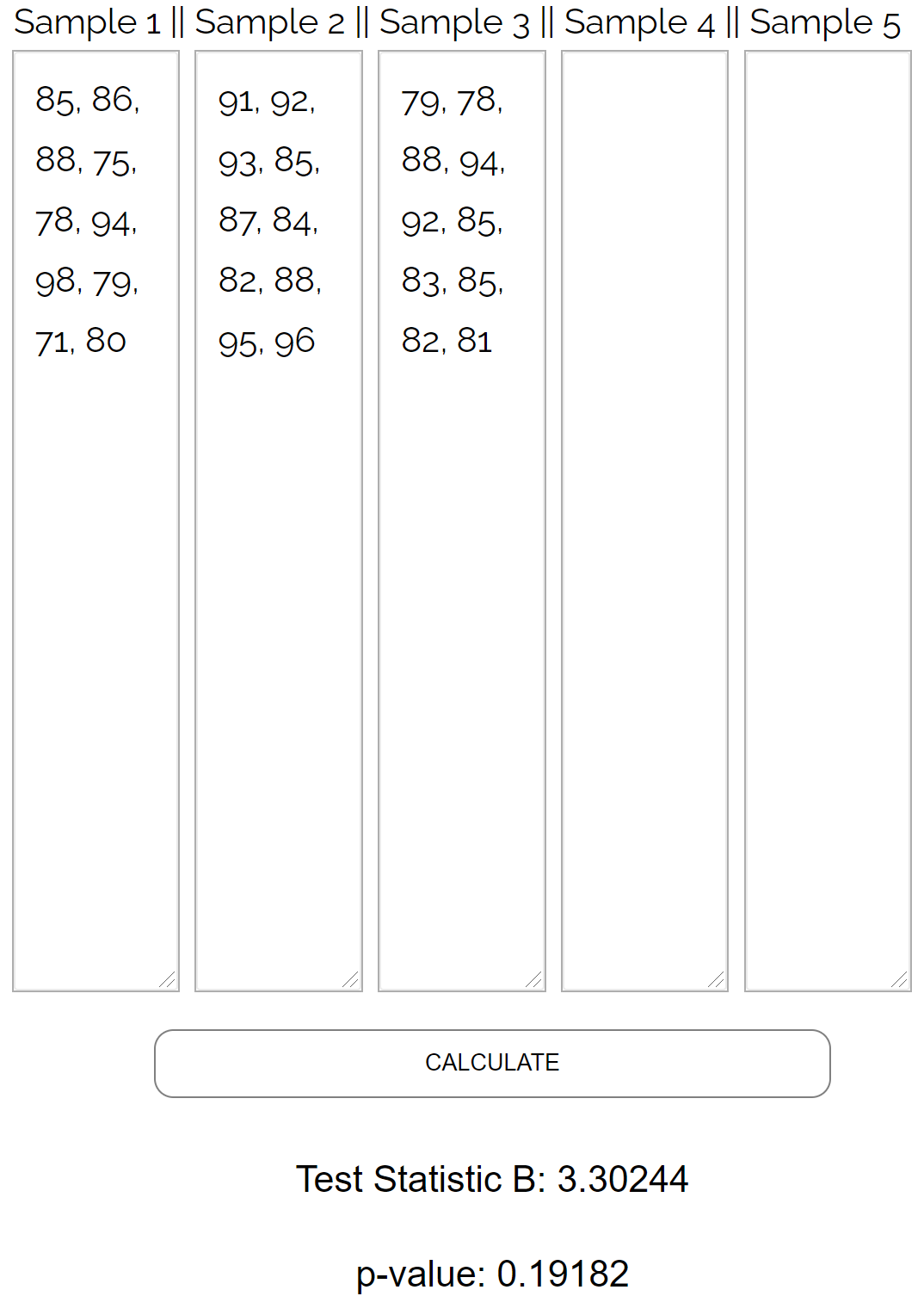
Test zwraca następujące wyniki:

• Statystyka testowa B : 3,30244
• Wartość P: 0,19182

Ponieważ wartość p jest nie mniejsza niż 0,05, profesorowi nie uda się odrzucić hipotezy zerowej. Innymi słowy, nie ma ona wystarczających dowodów, aby stwierdzić, że pomiędzy tymi trzema grupami występują różne luki.

W ten sposób może przystąpić do jednokierunkowej analizy ANOVA.

Dodatkowe zasoby

Jak wykonać test Bartletta w R (krok po kroku)
Jak wykonać test Bartletta w Pythonie (krok po kroku)