Test browna – forsythe’a w r: przykład krok po kroku
Jednoczynnikową analizę ANOVA stosuje się w celu określenia, czy istnieje istotna różnica pomiędzy średnimi z trzech lub większej liczby niezależnych grup.
Jednym z założeń jednokierunkowej analizy ANOVA jest to, że wariancje populacji, z których pobierane są próbki, są równe.
Jednym z najczęstszych sposobów sprawdzenia tego jest użycie testu Browna-Forsythe’a , który jest testem statystycznym wykorzystującym następujące założenia :
- H 0 : Wariancje pomiędzy populacjami są równe.
- H A : Różnice między populacjami nie są równe.
Jeśli wartość p testu jest poniżej pewnego poziomu istotności (np. α = 0,05), wówczas odrzucamy hipotezę zerową i stwierdzamy, że wariancje nie są równe pomiędzy różnymi populacjami.
W tym samouczku przedstawiono krok po kroku przykład wykonania testu Browna-Forsythe’a w języku R.
Krok 1: Wprowadź dane
Załóżmy, że chcielibyśmy wiedzieć, czy trzy różne programy ćwiczeń prowadzą do różnych poziomów utraty wagi.
Aby to przetestować, rekrutujemy 90 osób i losowo przydzielamy 30 do korzystania z każdego programu. Następnie po miesiącu mierzymy utratę wagi każdej osoby.
Poniższy zestaw danych zawiera informacje o ilości utraconej wagi w każdym programie:
#make this example reproducible set.seed(0) #create data frame data <- data.frame(program = as . factor ( rep (c(" A ", " B ", " C "), each = 30)), weight_loss = c( runif (30, 0, 3), runif (30, 0, 5), runif (30, 1, 7))) #view first six rows of data frame head(data) # program weight_loss #1 A 2.6900916 #2 A 0.7965260 #3 A 1.1163717 #4 A 1.7185601 #5 A 2.7246234 #6 A 0.6050458
Krok 2: Podsumuj i zwizualizuj dane
Przed wykonaniem testu Browna-Forsythe’a możemy utworzyć wykresy pudełkowe, aby zwizualizować wariancję utraty wagi dla każdej grupy:
boxplot(weight_loss ~ program, data = data)
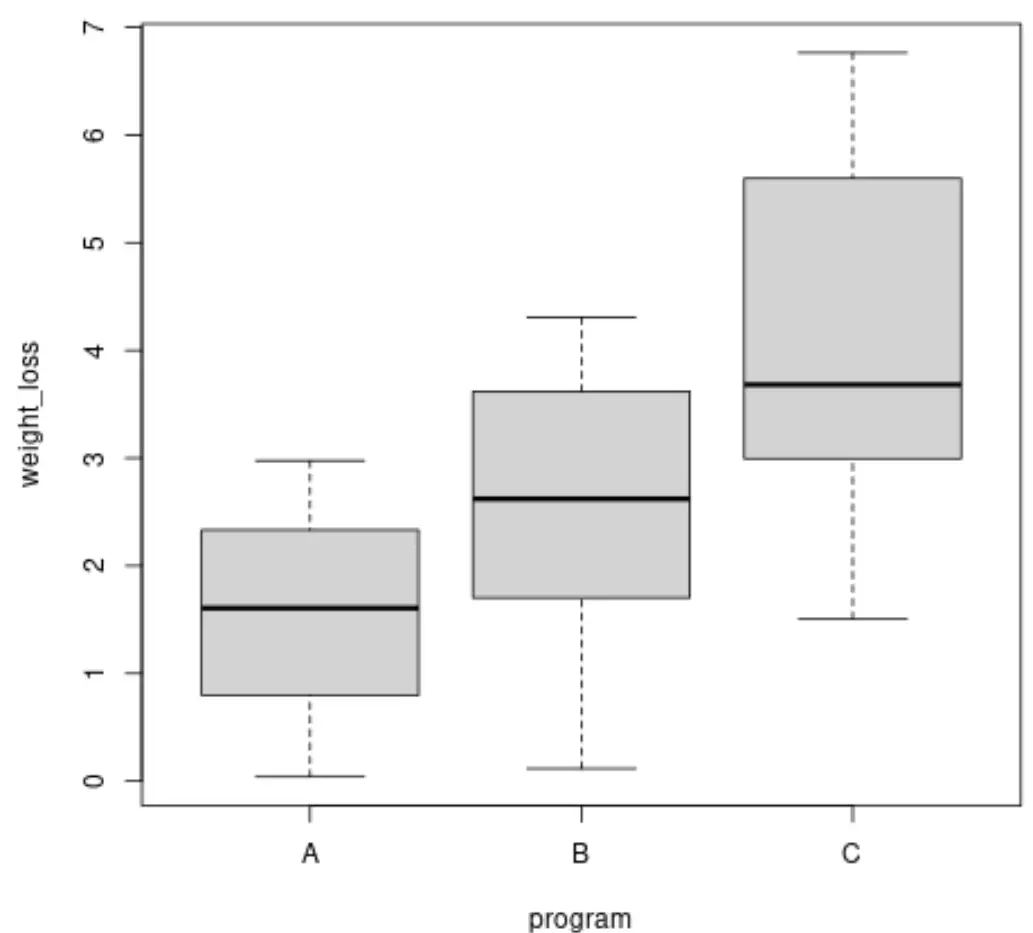
Możemy również obliczyć wariancję utraty wagi w każdej grupie:
#load dplyr package library (dplyr) #calculate variance of weight loss by group data %>% group_by (program) %>% summarize (var=var(weight_loss)) # A tibble: 3 x 2 program var 1 A 0.819 2 B 1.53 3 C 2.46
Widzimy, że wariancje między grupami się różnią, ale aby określić, czy różnice te są istotne statystycznie , możemy wykonać test Browna-Forsythe’a.
Krok 3: Wykonaj test Browna-Forsythe’a
Aby wykonać test Browna-Forsythe’a w R, możemy skorzystać z funkcji bf.test() z pakietu onewaytests :
#load onewaytests package library (onewaytests) #perform Brown-Forsythe test bf.test(weight_loss ~ program, data = data) Brown-Forsythe Test (alpha = 0.05) -------------------------------------------------- ----------- data: weight_loss and program statistic: 30.83304 num df: 2 name df: 74.0272 p.value: 1.816529e-10 Result: Difference is statistically significant. -------------------------------------------------- -----------
Wartość p testu okazuje się mniejsza niż 0,000 i jak pokazuje wynik, różnice w wariancjach pomiędzy trzema grupami są istotne statystycznie.
Następne kroki
Jeśli nie możesz odrzucić hipotezy zerowej testu Browna-Forsythe’a, możesz przeprowadzić jednoczynnikową analizę ANOVA na danych.
Jeśli jednak odrzucisz hipotezę zerową, oznacza to, że naruszone zostaje założenie o równości wariancji. W tym przypadku masz dwie możliwości:
1. Mimo to wykonaj jednokierunkową ANOVA.
Okazuje się, że jednokierunkowa analiza ANOVA jest w rzeczywistości odporna na nierówne wariancje, o ile największa wariancja nie jest większa niż 4-krotność najmniejszej wariancji.
W kroku 2 powyższego przykładu odkryliśmy, że najmniejsza wariancja wyniosła 0,819, a największa wariancja 2,46. Zatem stosunek największej do najmniejszej wariancji wynosi 2,46 / 0,819 = 3,003 .
Ponieważ ta wartość jest mniejsza niż 4, możemy po prostu wykonać jednokierunkową ANOVA.
2. Wykonaj test Kruskala-Wallisa
Jeżeli stosunek największej wariancji do najmniejszej wariancji jest większy niż 4, można zamiast tego wykonać test Kruskala-Wallisa . Uważa się to za nieparametryczny odpowiednik jednokierunkowej analizy ANOVA.
Przykładowy przykład testu Kruskala-Wallisa w języku R znajdziesz tutaj .