Jak wykonać test dobroci dopasowania chi square w spss

Test dobroci dopasowania chi-kwadrat służy do określenia, czy zmienna kategoryczna ma rozkład hipotetyczny.

W tym samouczku wyjaśniono, jak przeprowadzić test dobroci dopasowania chi-kwadrat w programie SPSS.

Przykład: test dobroci dopasowania chi-kwadrat w SPSS

Właściciel sklepu twierdzi, że w każdym dniu tygodnia do jego sklepu przychodzi taka sama liczba klientów. Aby przetestować tę hipotezę, badacz rejestruje liczbę klientów, którzy przychodzą do sklepu w danym tygodniu i stwierdza, co następuje:

• Poniedziałek: 50 klientów
• Wtorek: 60 klientów
• Środa: 40 klientów
• Czwartek: 47 klientów
• Piątek: 53 klientów

Wykonaj poniższe kroki, aby przeprowadzić test dobroci dopasowania chi-kwadrat w programie SPSS w celu ustalenia, czy dane są zgodne z twierdzeniami właściciela sklepu.

Krok 1: Wprowadź dane.

Najpierw wprowadź dane do SPSS w następującym formacie:

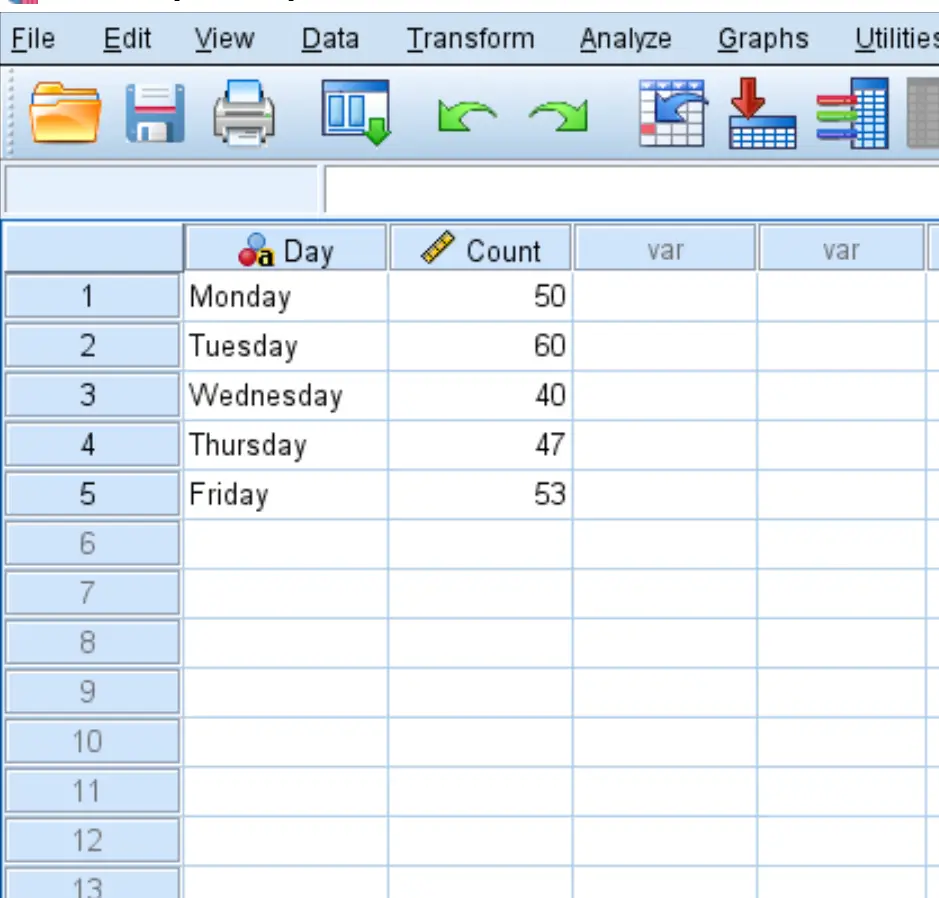
Krok 2: Użyj ważonych pudełek.

Aby test zadziałał poprawnie należy poinformować SPSS, że zmienna „Dzień” powinna być ważona zmienną „Numer”.

Kliknij kartę Dane , a następnie opcję Przypadki wagowe :

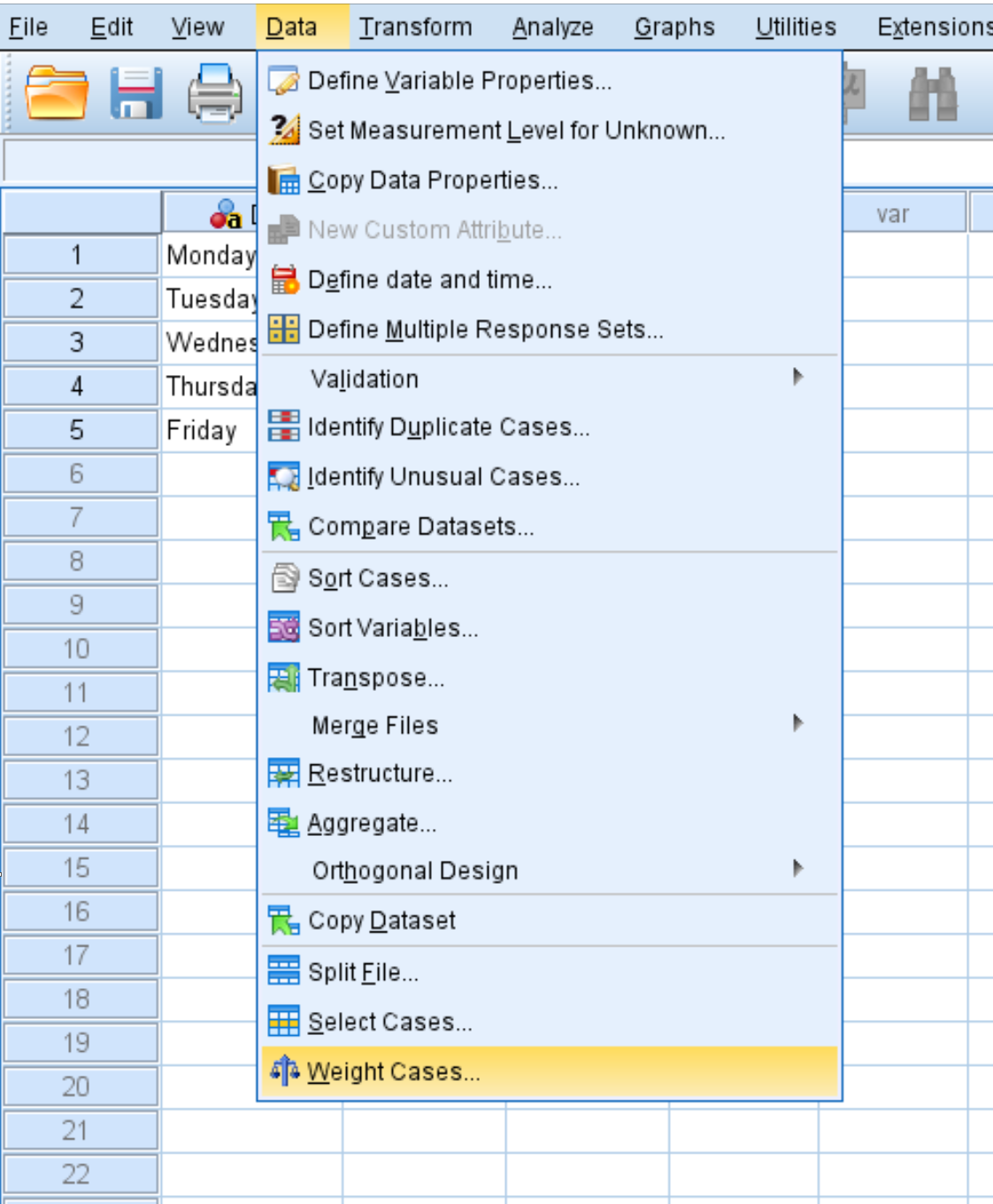
W nowym oknie, które się pojawi, przeciągnij zmienną Count do obszaru oznaczonego Lista zmiennych testowych. Następnie kliknij OK .

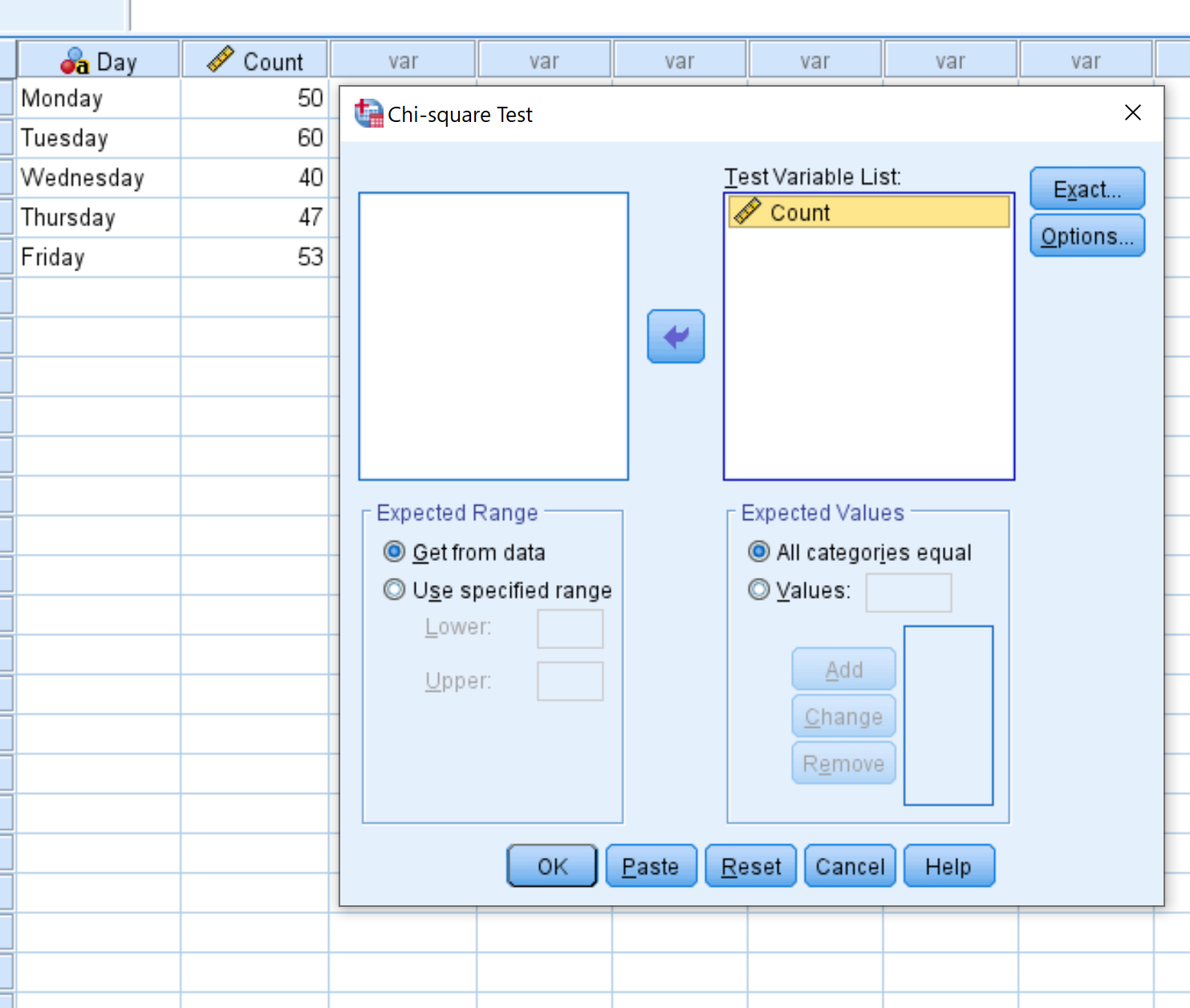
Krok 3: Wykonaj test dobroci dopasowania chi-kwadrat.

Kliknij kartę Analiza , następnie Testy nieparametryczne , następnie Starsze okna dialogowe , a następnie Chi-kwadrat :

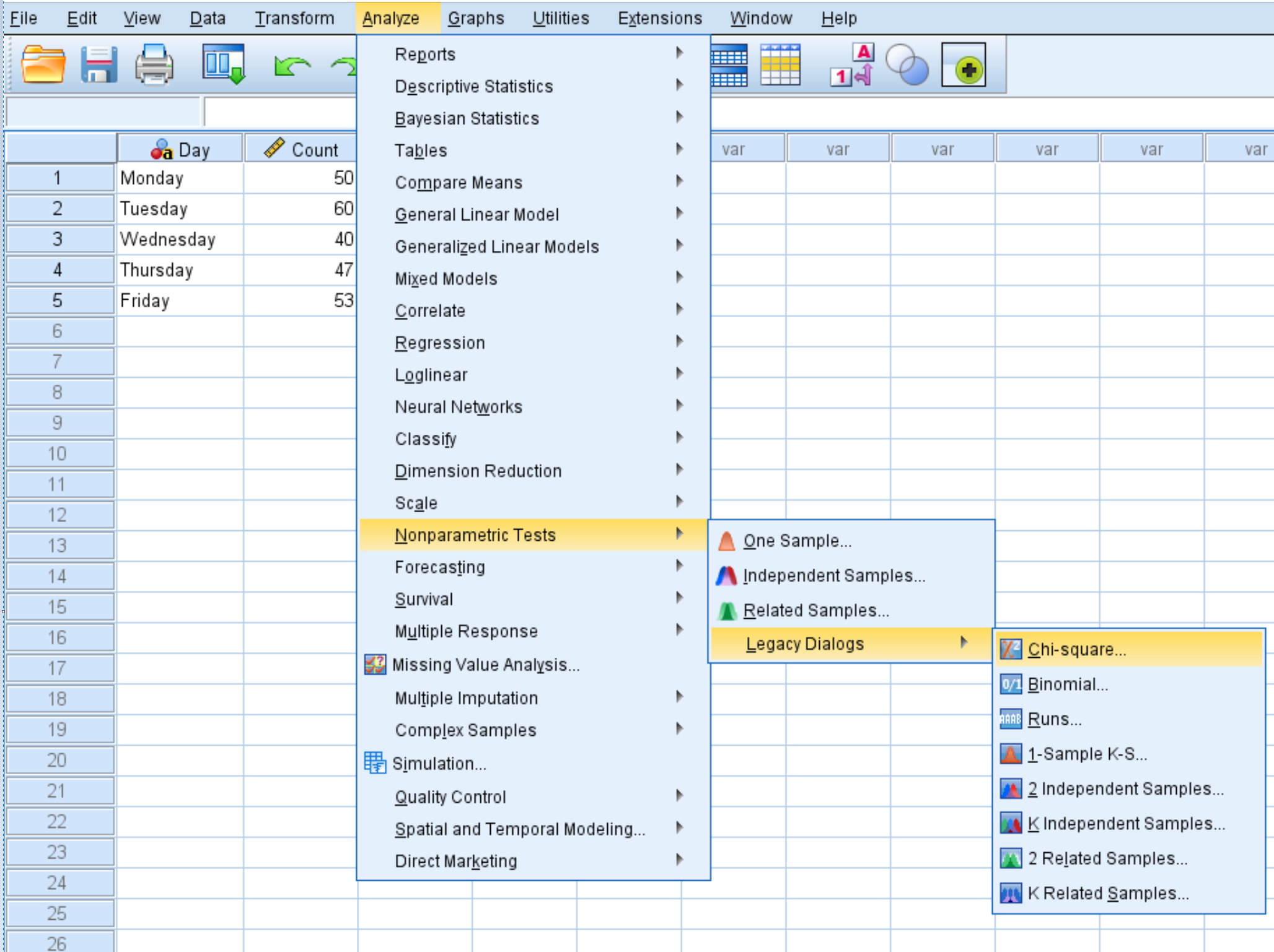
W nowym oknie, które się pojawi, przeciągnij zmienną Count do obszaru oznaczonego Lista zmiennych testowych.

Pozostaw etykietę zaznaczoną obok Wszystkie kategorie równe , ponieważ każda z naszych kategorii (tj. dni tygodnia) ma tę samą oczekiwaną liczbę odwiedzających każdego dnia. Następnie kliknij OK .

Krok 4: Interpretacja wyników .

Po kliknięciu OK pojawią się wyniki testu zgodności chi-kwadrat:

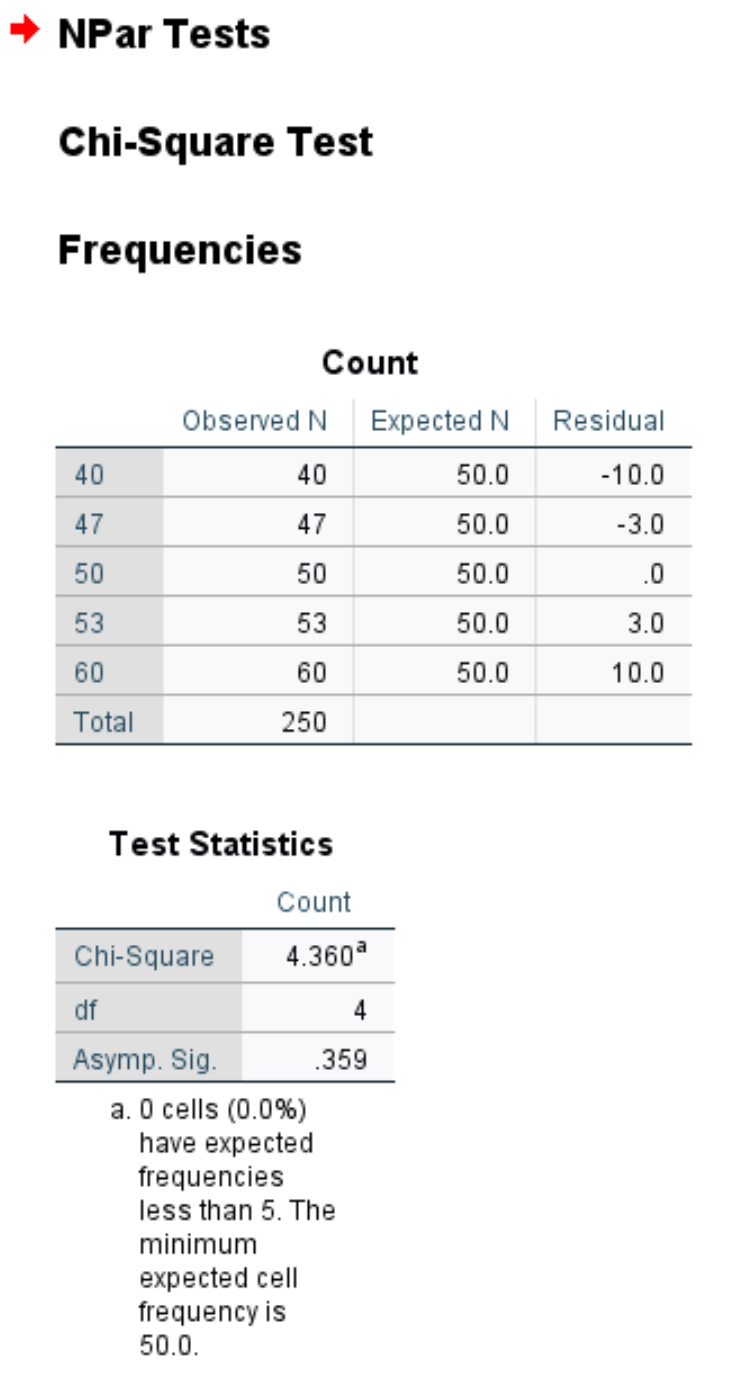
Pierwsza tabela przedstawia obserwowaną i oczekiwaną liczbę klientów w każdym dniu tygodnia, a także resztę (tj. różnicę) między obserwowaną a oczekiwaną.

Druga tabela wyświetla następujące liczby:

Chi-kwadrat: Statystyka testu chi-kwadrat, która wynosi 4,36.

df: Stopnie swobody obliczane jako #kategorie-1 = 5-1 = 4.

Asymp. Sig: Wartość p odpowiadająca wartości Chi-kwadrat wynoszącej 4,36 z 4 stopniami swobody, czyli 0,359. Wartość tę można również znaleźć za pomocą kalkulatora wyniku chi-kwadrat do wartości P.

Ponieważ wartość p (0,359) jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej. Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że prawdziwy rozkład klientów różni się od tego podawanego przez właściciela sklepu.