4 przykłady wykorzystania testów chi-kwadrat w prawdziwym życiu
W statystyce istnieją dwa różne typy testów Chi-kwadrat:
1. Test dobroci dopasowania chi-kwadrat – używany do określenia, czy zmienna kategoryczna ma rozkład hipotetyczny.
2. Test niezależności Chi-kwadrat – używany do określenia, czy istnieje istotny związek pomiędzy dwiema zmiennymi kategorycznymi.
W tym artykule przedstawiamy kilka przykładów wykorzystania każdego z typów testów chi-kwadrat w rzeczywistych sytuacjach.
Przykład 1: Test dobroci dopasowania chi-kwadrat
Załóżmy, że właściciel sklepu twierdzi, że każdego dnia tygodnia do jego sklepu przychodzi taka sama liczba klientów.
Aby przetestować tę hipotezę, rejestruje liczbę klientów, którzy przychodzą do sklepu w danym tygodniu i stwierdza, co następuje:
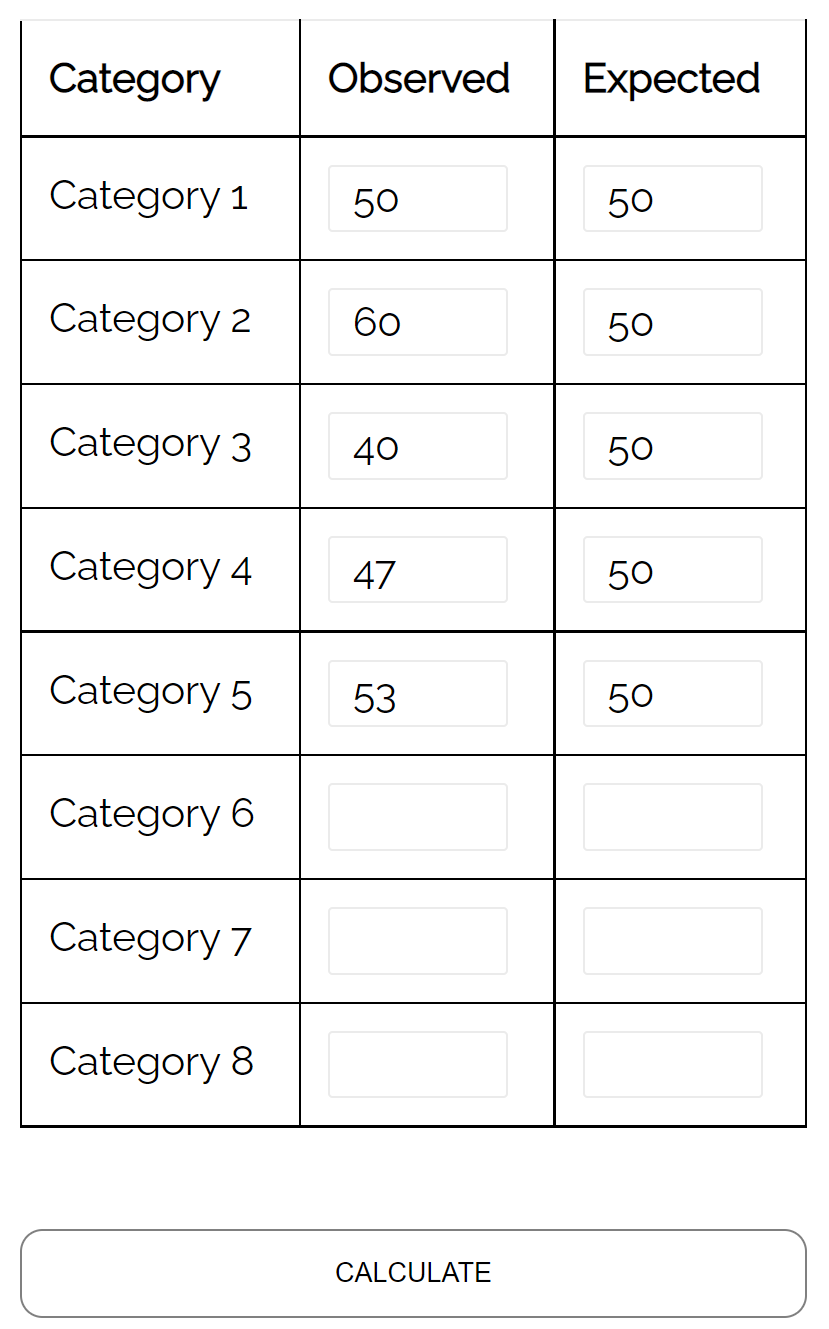
- Poniedziałek: 50 klientów
- Wtorek: 60 klientów
- Środa: 40 klientów
- Czwartek: 47 klientów
- Piątek: 53 klientów
Może zastosować test dobroci dopasowania chi-kwadrat, aby określić, czy rozkład klientów, którzy przychodzą każdego dnia, jest zgodny z jego hipotezą dotyczącą rozkładu.
Korzystając z kalkulatora testu dobroci dopasowania chi-kwadrat , może stwierdzić, że wartość p testu wynosi 0,359 .

Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie ma wystarczających dowodów, aby twierdzić, że prawdziwy rozkład klientów różni się od tego, który twierdzi właściciel sklepu.
Przykład 2: Test dobroci dopasowania chi-kwadrat
Załóżmy, że biolog twierdzi, że co tydzień taka sama liczba czterech różnych gatunków jeleni wchodzi na pewien zalesiony obszar lasu.
Aby przetestować tę hipotezę, rejestruje liczbę każdego gatunku jelenia, który pojawia się na zalesionym obszarze w ciągu tygodnia:
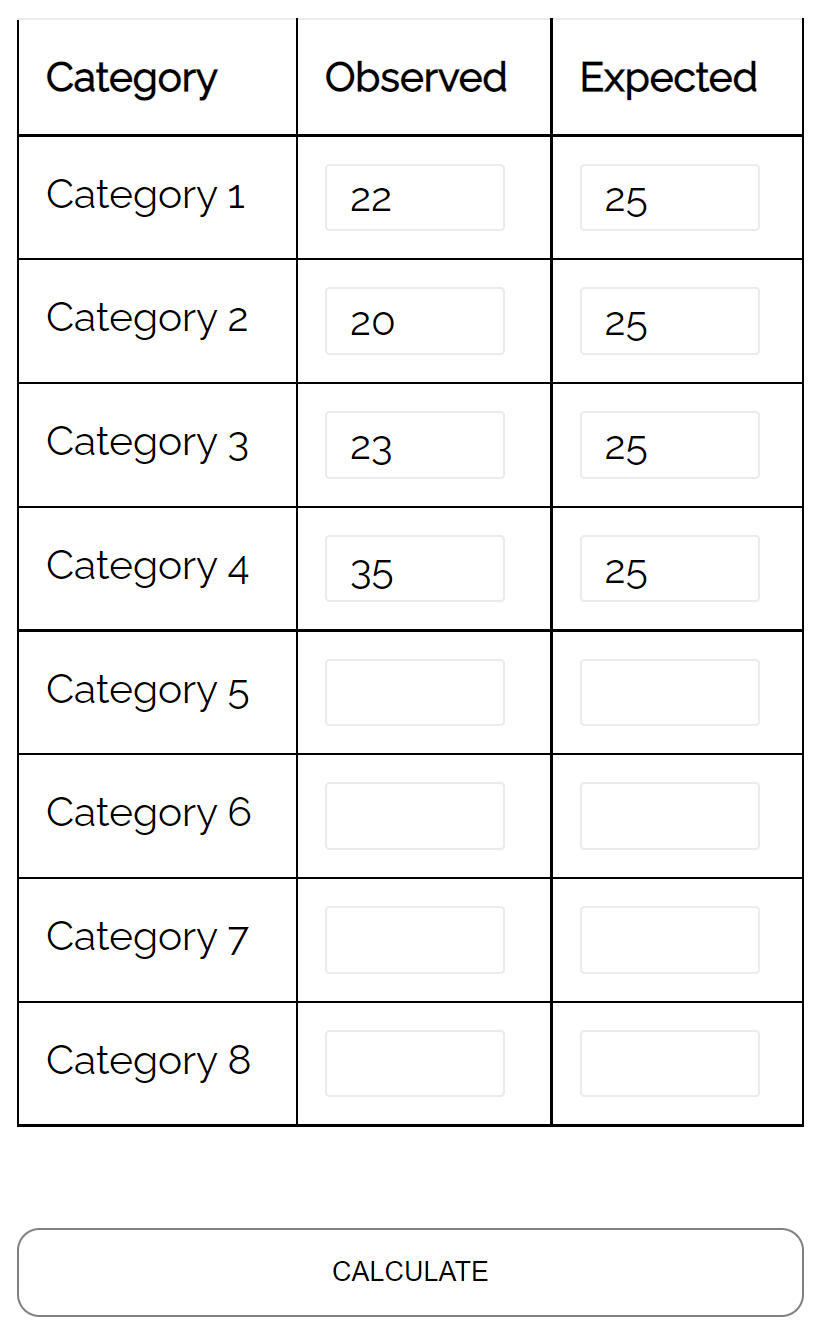
- Gatunek nr 1: 22
- Gatunek nr 2: 20
- Gatunek nr 3: 23
- Gatunek nr 4: 35
Potrafi zastosować test dobroci dopasowania chi-kwadrat, aby określić, czy rozmieszczenie gatunków jeleniowatych, które co tydzień wchodzą na zalesiony obszar lasu, jest zgodne z jego hipotetycznym rozmieszczeniem.
Korzystając z kalkulatora testu dobroci dopasowania chi-kwadrat , widzi, że wartość p dla testu wynosi 0,137 .
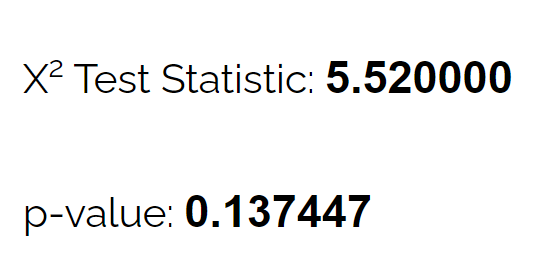
Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie ma wystarczających dowodów, aby twierdzić, że prawdziwe rozmieszczenie jeleniowatych różni się od tego, co twierdzi biolog.
Przykład 3: Test niezależności chi-kwadrat
Załóżmy, że decydent w pewnym mieście chce wiedzieć, czy płeć jest powiązana z preferencjami partii politycznej.
Postanawia pobrać prostą losową próbę 500 wyborców i zapytać ich o preferencje dotyczące partii politycznych. Wyniki badania prezentuje poniższa tabela:
| Republikański | Demokrata | Niezależny | Całkowity | |
| Mężczyzna | 120 | 90 | 40 | 250 |
| Kobieta | 110 | 95 | 45 | 250 |
| Całkowity | 230 | 185 | 85 | 500 |
Może zastosować test niezależności chi-kwadrat, aby określić, czy istnieje statystycznie istotny związek między dwiema zmiennymi.
Korzystając z kalkulatora testu niezależności chi-kwadrat , może stwierdzić, że wartość p testu wynosi 0,649 .
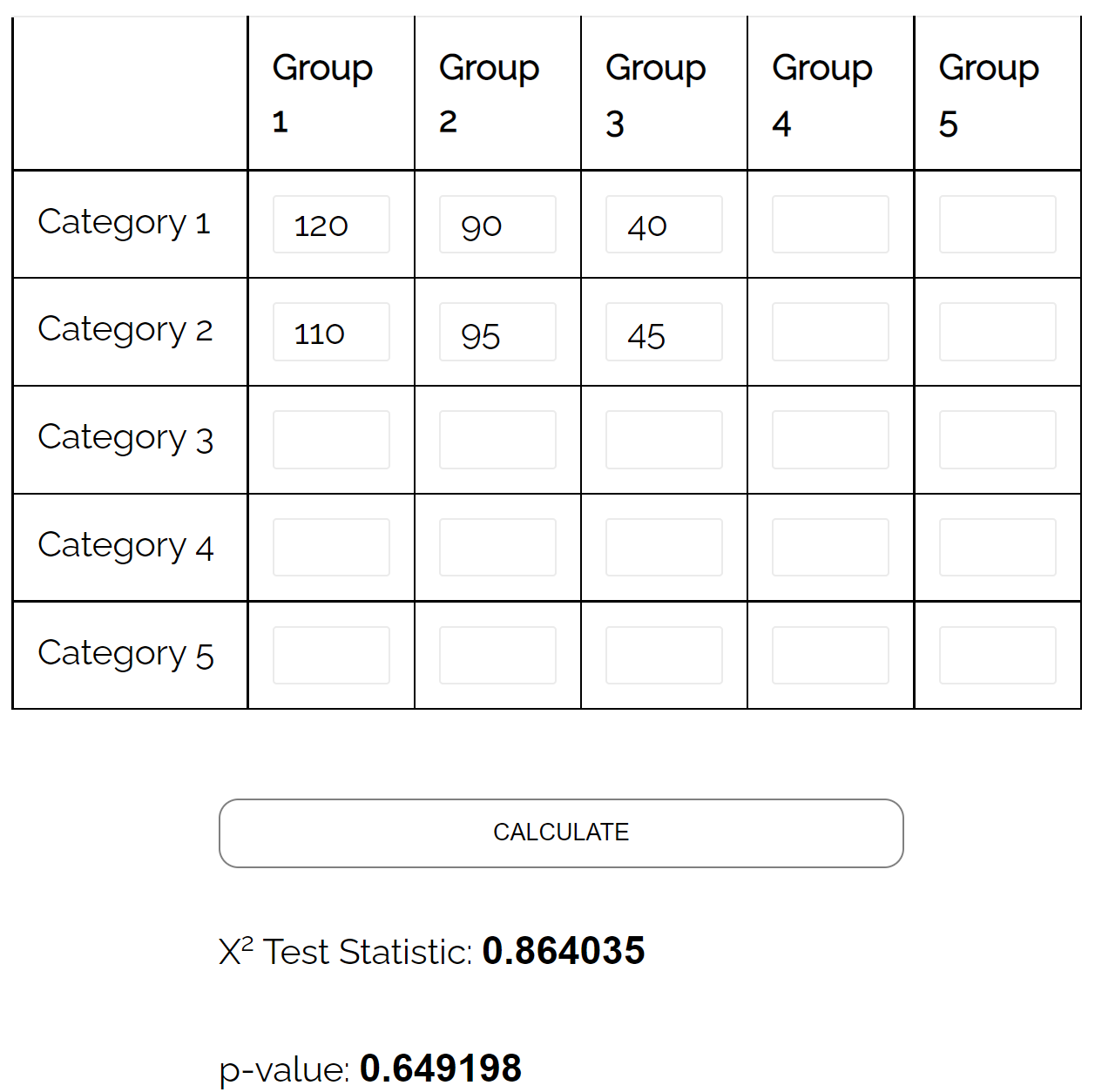
Ponieważ wartość p jest nie mniejsza niż 0,05, nie ma wystarczających dowodów na to, że istnieje związek między płcią a preferencjami partii politycznych.
Przykład 4: Test niezależności chi-kwadrat
Załóżmy, że badacz chce wiedzieć, czy stan cywilny jest powiązany z poziomem wykształcenia.
Postanawia pobrać prostą losową próbę składającą się z 300 osób i otrzymuje następujące wyniki:
| Liceum | Licencjaci | Mistrz lub wyższy | Całkowity | |
| Żonaty | 20 | 100 | 35 | 155 |
| Licencjat | 50 | 80 | 15 | 145 |
| Całkowity | 70 | 180 | 50 | 300 |
Może zastosować test niezależności chi-kwadrat, aby określić, czy istnieje statystycznie istotny związek między dwiema zmiennymi.
Korzystając z kalkulatora testu niezależności chi-kwadrat , może zobaczyć, że wartość p testu wynosi 0,000011 .
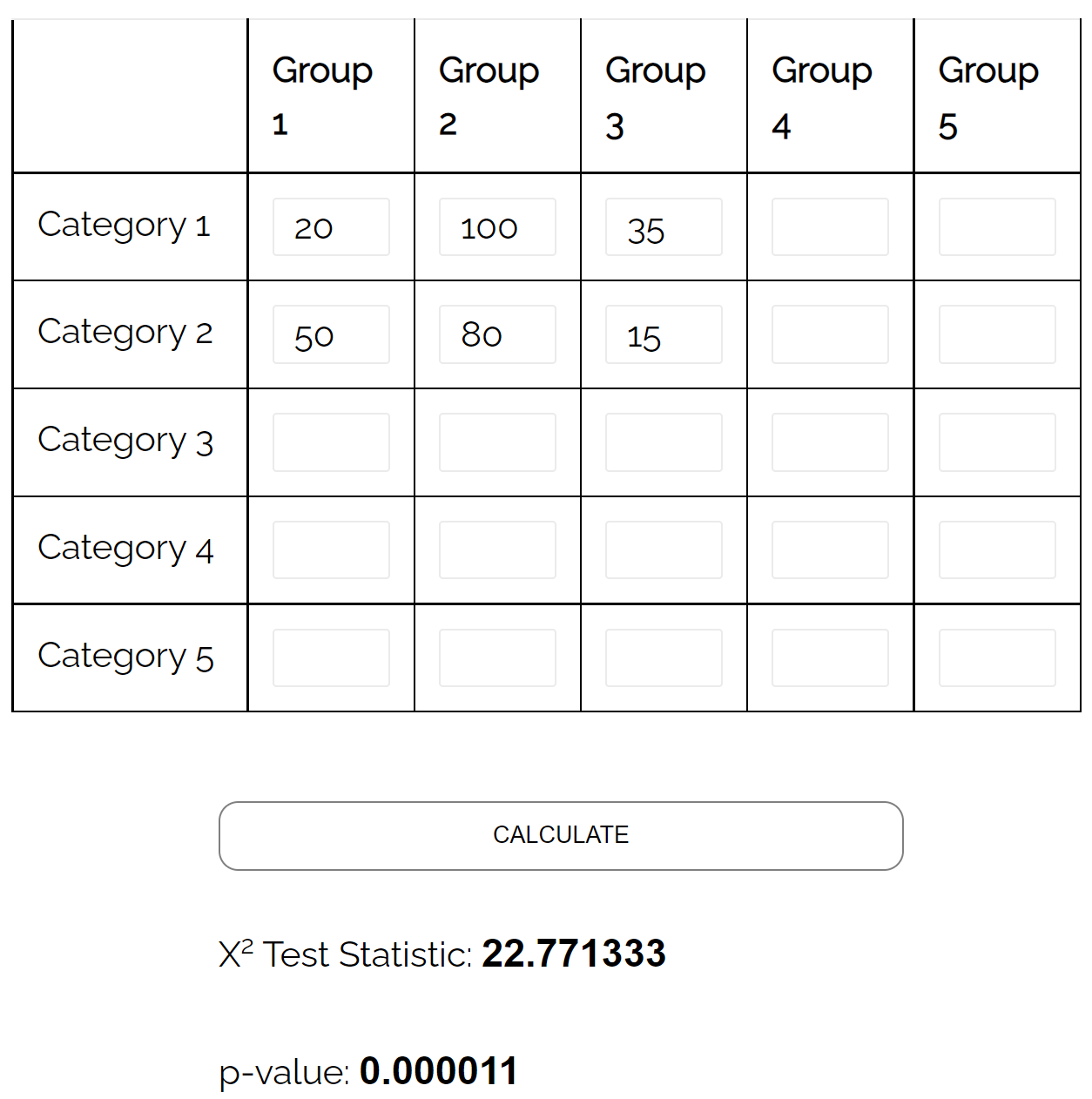
Ponieważ wartość p jest mniejsza niż 0,05, istnieją wystarczające dowody na to, że istnieje związek między stanem cywilnym a poziomem wykształcenia.
Dodatkowe zasoby
Poniższe samouczki stanowią wprowadzenie do różnych typów testów chi-kwadrat:
Poniższe tutoriale wyjaśniają różnicę pomiędzy testami Chi-kwadrat i innymi testami statystycznymi: