Jak wykonać test cramera-vona misesa w r (z przykładami)

Test Cramera-Vona Misesa służy do określenia, czy próbka pochodzi z rozkładu normalnego .

Ten typ testu jest przydatny do ustalenia, czy dany zbiór danych pochodzi z rozkładu normalnego, co jest powszechnie stosowanym założeniem w wielu testach statystycznych, w tym w regresji , ANOVA , testach t i wielu innych. 'inni.

Test Cramera-Von Misesa możemy łatwo wykonać, korzystając z funkcji cvm.test() z pakietu goftest w R.

Poniższy przykład pokazuje, jak w praktyce wykorzystać tę funkcję.

Przykład 1: Test Cramera-Vona Misesa na normalnych danych

Poniższy kod pokazuje, jak przeprowadzić test Cramera-Vona Misesa na zbiorze danych o wielkości próby n=100:

 library (goftest)

#make this example reproducible
set. seeds (0)

#create dataset of 100 random values generated from a normal distribution
data <- rnorm(100)

#perform Cramer-Von Mises test for normality
cvm. test (data, ' pnorm ')

	Cramer-von Mises test of goodness-of-fit
	Null hypothesis: Normal distribution
	Parameters assumed to be fixed

data:data
omega2 = 0.078666, p-value = 0.7007

Wartość p testu wynosi 0,7007 .

Ponieważ wartość ta jest nie mniejsza niż 0,05, możemy założyć, że przykładowe dane pochodzą z populacji o rozkładzie normalnym.

Wynik ten nie powinien dziwić, gdyż przykładowe dane wygenerowaliśmy za pomocą funkcji rnorm() , która generuje losowe wartości ze standardowego rozkładu normalnego .

Powiązane: Przewodnik po dnorm, pnorm, qnorm i rnorm w R

Możemy również utworzyć histogram, aby wizualnie sprawdzić, czy przykładowe dane mają rozkład normalny:

 hist(data, col=' steelblue ') 

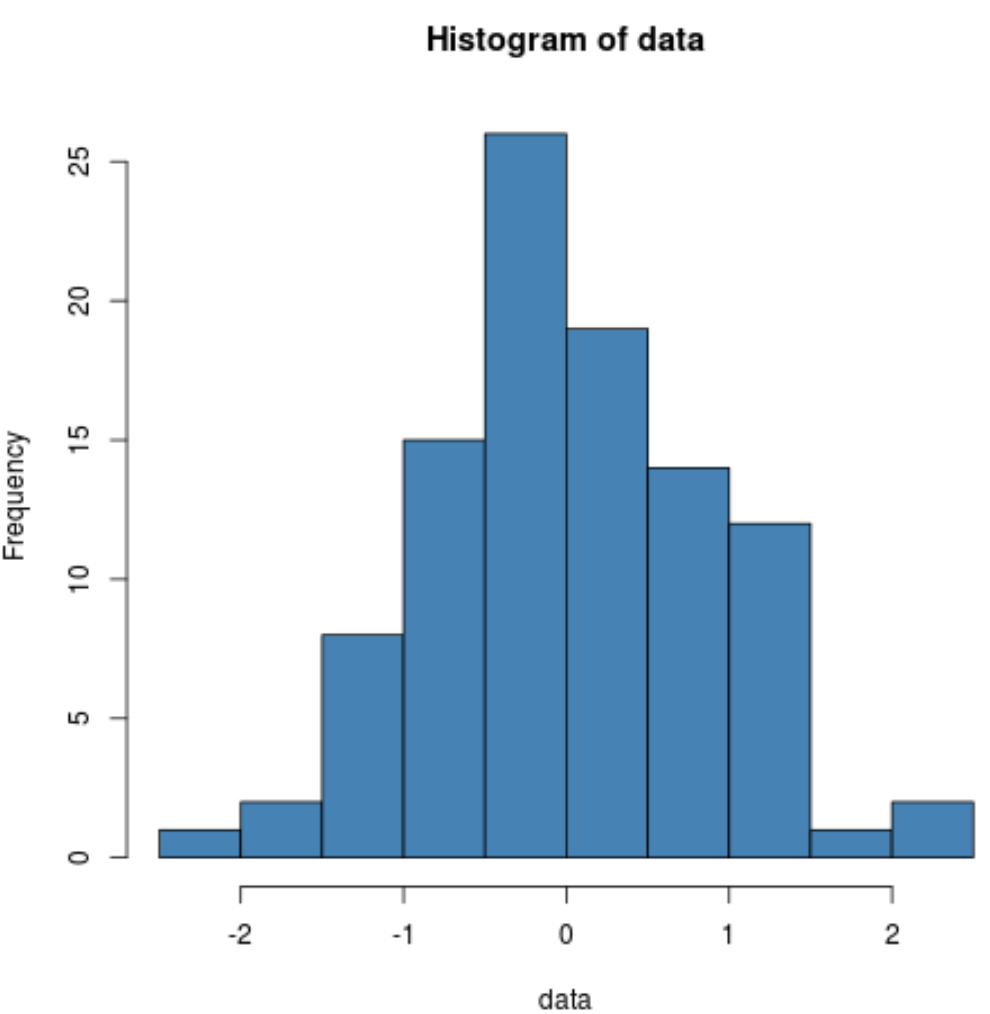
Widzimy, że rozkład ma kształt dzwonu z pikiem w środku rozkładu, co jest typowe dla danych o rozkładzie normalnym.

Przykład 2: Test Cramera-Vona Misesa na danych nietypowych

Poniższy kod pokazuje jak przeprowadzić test Cramera-Vona Misesa na zbiorze danych o wielkości próby 100, w którym wartości są generowane losowo z rozkładu Poissona :

 library (goftest)

#make this example reproducible
set. seeds (0)

#create dataset of 100 random values generated from a Poisson distribution
data <- rpois(n=100, lambda=3)

#perform Cramer-Von Mises test for normality
cvm. test (data, ' pnorm ')

	Cramer-von Mises test of goodness-of-fit
	Null hypothesis: Normal distribution
	Parameters assumed to be fixed

data:data
omega2 = 27.96, p-value < 2.2e-16

Wartość p testu okazuje się wyjątkowo niska.

Ponieważ wartość ta jest mniejsza niż 0,05, mamy wystarczające dowody, aby stwierdzić, że dane próbki nie pochodzą z populacji o rozkładzie normalnym.

Wynik ten nie powinien dziwić, gdyż przykładowe dane wygenerowaliśmy za pomocą funkcji rpois() , która generuje wartości losowe z rozkładu Poissona.

Powiązane: Przewodnik po dpois, ppois, qpois i rpois w R

Możemy również utworzyć histogram, aby wizualnie zobaczyć, że przykładowe dane nie mają rozkładu normalnego:

 hist(data, col=' coral2 ') 

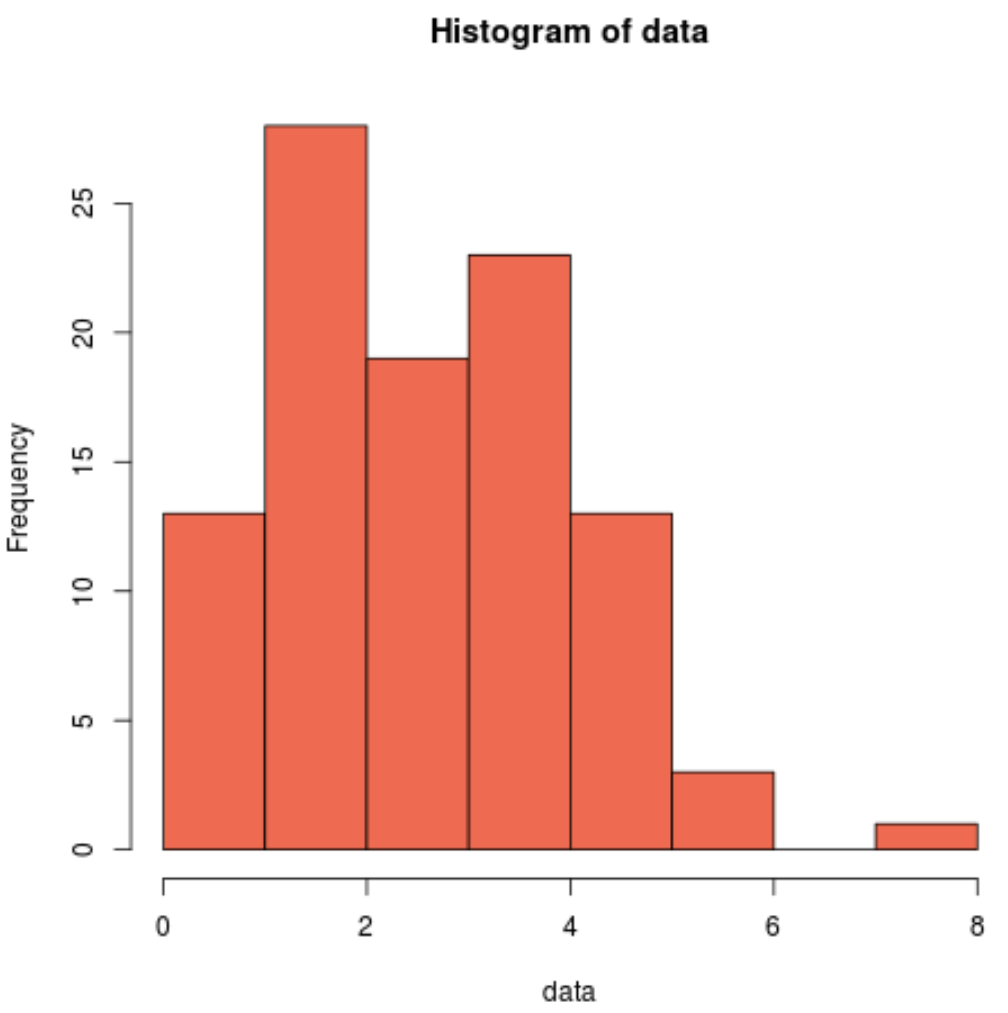
Widzimy, że rozkład jest prawoskośny i nie ma typowego „kształtu dzwonu” kojarzonego z rozkładem normalnym.

Zatem nasz histogram odpowiada wynikom testu Cramera-Von Misesa i potwierdza, że nasze przykładowe dane nie pochodzą z rozkładu normalnego.

Co zrobić z nietypowymi danymi

Jeśli dany zbiór danych nie ma rozkładu normalnego, często możemy wykonać jedną z następujących transformacji, aby uczynić go bardziej normalnym:

1. Transformacja logu: przekształć zmienną odpowiedzi z y na log(y) .

2. Transformacja pierwiastka kwadratowego: Przekształć zmienną odpowiedzi z y na √y .

3. Transformacja pierwiastka sześciennego: przekształć zmienną odpowiedzi z y na y ^1/3 .

Wykonując te przekształcenia, zmienna odpowiedzi ogólnie zbliża się do rozkładu normalnego.

Zapoznaj się z tym samouczkiem, aby zobaczyć, jak wykonać te przekształcenia w praktyce.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonać inne testy normalności w R:

Jak wykonać test Shapiro-Wilka w R
Jak wykonać test Andersona-Darlinga w R
Jak wykonać test Kołmogorowa-Smirnowa w R