Jak używać testu dunnetta do porównań wielokrotnych
ANOVA (analiza wariancji) służy do określenia, czy istnieje statystycznie istotna różnica między średnimi z trzech lub więcej niezależnych grup.
Jeżeli wartość p analizy ANOVA jest poniżej pewnego wybranego poziomu istotności, możemy odrzucić hipotezę zerową i stwierdzić, że mamy wystarczające dowody, aby stwierdzić, że przynajmniej jedna ze średnich grupowych różni się od pozostałych.
Nie mówi nam to jednak , które grupy różnią się od siebie. To po prostu mówi nam, że nie wszystkie średnie grupowe są równe. Aby dokładnie wiedzieć, które grupy się od siebie różnią, musimy przeprowadzićtest post-hoc .
Jeżeli jedną z grup w badaniu uznamy za grupę kontrolną , wówczas powinniśmy zastosować test Dunnetta jako test post hoc po ANOVA.
Test Dunnetta: definicja
Aby przeprowadzić test Dunnetta, możemy wykonać następujące dwa kroki:
Krok 1: Znajdź wartość krytyczną Dunnetta.
Najpierw musimy znaleźć wartość krytyczną Dunnetta. Oblicza się to w następujący sposób:
Wartość krytyczna Dunnetta: t d √ 2MS w /n
Złoto:
- t d : Wartość znaleziona w tabeli Dunnetta dla danego poziomu alfa, liczby grup i wielkości próbek grupowych.
- MS w : Średnie kwadraty „w grupie” w tabeli wyjściowej ANOVA
- n: wielkość próby grupowej
Krok 2: Porównaj różnice między średnimi grupowymi a wartością krytyczną Dunnetta.
Następnie obliczamy bezwzględną różnicę między średnią w każdej grupie a średnią w grupie kontrolnej. Jeśli różnica przekracza wartość krytyczną Dunnetta, wówczas różnicę tę uważa się za istotną statystycznie.
Poniższy przykład pokazuje, jak w praktyce przeprowadzić test Dunnetta.
Test Dunnetta: przykład
Załóżmy, że nauczycielka chce wiedzieć, czy dwie nowe techniki uczenia się mogą poprawić wyniki jej uczniów w testach. Aby to sprawdzić, losowo dzieli swoją klasę składającą się z 30 uczniów na trzy następujące grupy:
- Grupa kontrolna: 10 uczniów
- Nowe studium techniczne 1: 10 studentów
- Nowe studium techniczne 2: 10 studentów
Po tygodniu stosowania przypisanej mu techniki nauki każdy uczeń przystępuje do tego samego egzaminu. Wyniki są następujące:
- Średni wynik egzaminu grupy kontrolnej: 81,6
- Średni wynik egzaminu dla grupy 1 nowej techniki nauki: 85,8
- Średni wynik z egzaminu grupowego New Study Technique 2: 87,7
- Średnie kwadraty „W obrębie grupy” w tabeli wyników ANOVA: 23,3
Mając te informacje, możemy wykonać test Dunnetta, aby ustalić, czy jedna z dwóch nowych technik badania daje znacząco różne średnie wyniki egzaminu niż grupa kontrolna.
Krok 1: Znajdź wartość krytyczną Dunnetta.
Przyjmując α = 0,05, wielkość próby grupowej n = 10 i sumę grupy = 3, tabela Dunnetta mówi nam, że do obliczenia wartości krytycznej należy użyć wartości 2,57 .
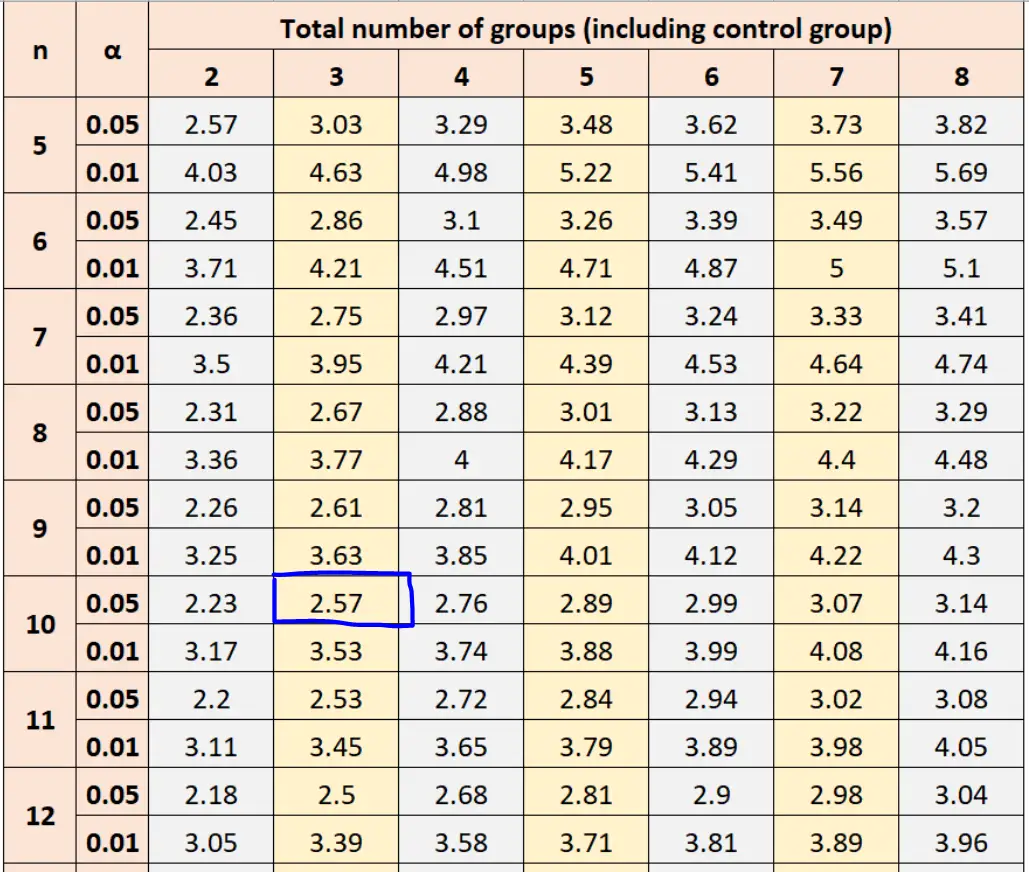
Następnie możemy podłączyć tę liczbę do wzoru, aby znaleźć krytyczną wartość Dunnetta:
Wartość krytyczna Dunnetta: t d √ 2MS w /n = 2,57√ 2(23,3)/10 = 5,548
Krok 2: Porównaj różnice między średnimi grupowymi a wartością krytyczną Dunnetta.
Bezwzględne różnice między średnimi każdej techniki badawczej a średnimi grupy kontrolnej są następujące:
- Abs. różnica pomiędzy nową techniką 1 a kontrolą: |85,8 – 81,6| = 4,2
- Abs. różnica pomiędzy nową techniką 2 a kontrolą: |87,7 – 81,6| = 6,1
Tylko bezwzględna różnica między techniką 2 a grupą kontrolną jest większa niż wartość krytyczna Dunnetta wynosząca 5548 .
Zatem możemy powiedzieć, że nowa technika badania nr 2 daje znacząco odmienne wyniki badań w porównaniu z grupą kontrolną, ale nie jest tak w przypadku nowej techniki badania nr 1.
Dodatkowe zasoby
Wprowadzenie do jednokierunkowej ANOVA
Przewodnik po korzystaniu z testów post-hoc z ANOVA
Jak wykonać test Dunnetta w R