Jak wykonać test dunnetta w r

Test post hoc to rodzaj testu przeprowadzanego po analizie ANOVA w celu ustalenia, które średnie grupowe różnią się od siebie statystycznie istotnie.

Jeżeli jedną z grup badawczych uznamy za grupę kontrolną , wówczas jako test post-hoc powinniśmy zastosować test Dunnetta .

W tym samouczku wyjaśniono, jak wykonać test Dunnetta w języku R.

Przykład: test Dunnetta w R

Załóżmy, że nauczycielka chce wiedzieć, czy dwie nowe techniki uczenia się mogą poprawić wyniki jej uczniów w testach. Aby to sprawdzić, losowo dzieli swoją klasę składającą się z 30 uczniów na trzy następujące grupy:

• Grupa kontrolna: 10 uczniów
• Nowe studium techniczne 1: 10 studentów
• Nowe studium techniczne 2: 10 studentów

Po tygodniu stosowania przypisanej mu techniki nauki każdy uczeń przystępuje do tego samego egzaminu.

Możemy wykonać następujące kroki w języku R, aby utworzyć zbiór danych, zwizualizować średnie grupowe, wykonać jednokierunkową analizę ANOVA i na koniec wykonać test Dunnetta, aby określić, która nowa technika badania (jeśli istnieje) daje inne wyniki w porównaniu z grupą kontrolną .

Krok 1: Utwórz zbiór danych.

Poniższy kod pokazuje, jak utworzyć zbiór danych zawierający wyniki egzaminów wszystkich 30 uczniów:

 #create data frame
data <- data.frame(technique = rep (c("control", "new1", "new2"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 control 76
2 controls 77
3 controls 77
4 controls 81
5 controls 82
6 controls 82

Krok 2: Wyświetl wyniki egzaminu dla każdej grupy.

Poniższy kod pokazuje, jak utworzyć wykresy skrzynkowe w celu wizualizacji rozkładu wyników egzaminu dla każdej grupy:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

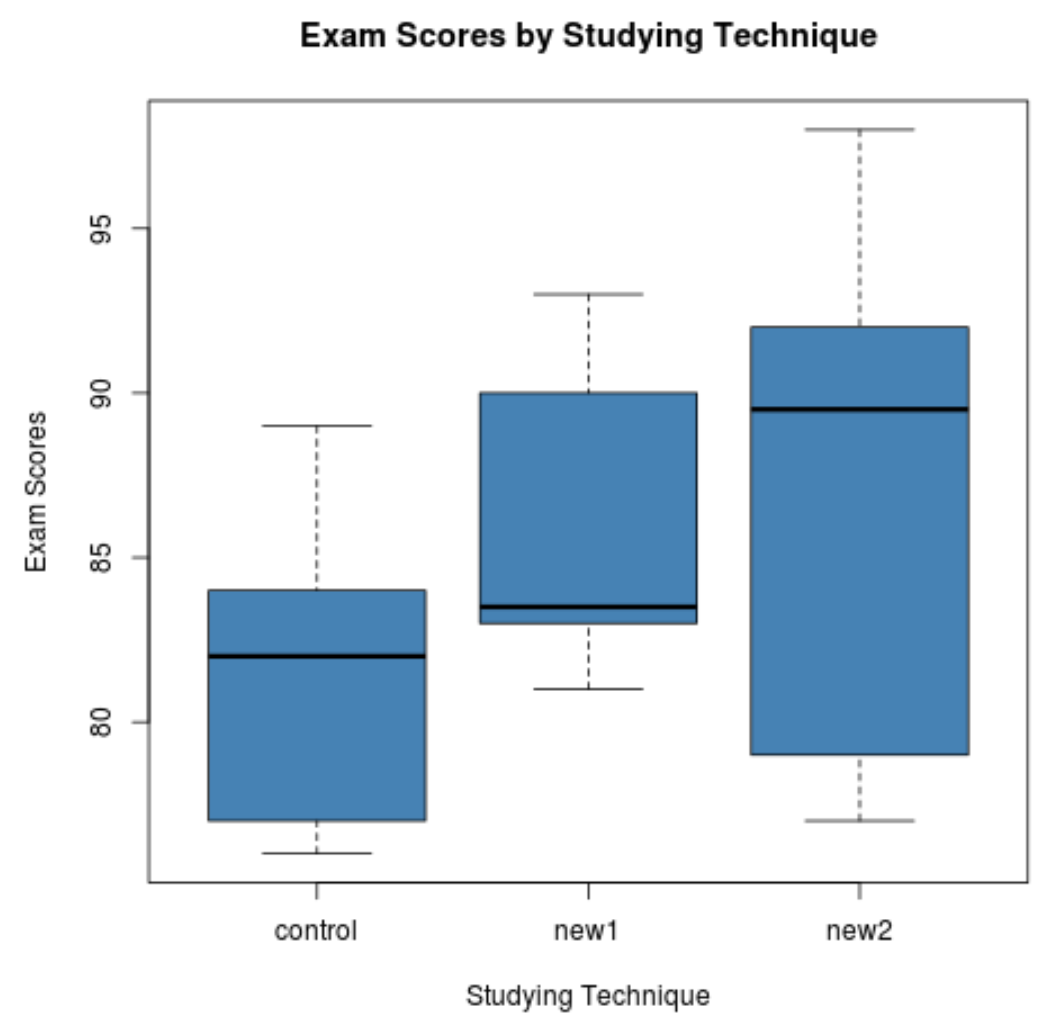
Już na podstawie wykresów pudełkowych widać, że rozkład wyników egzaminów jest bardzo różny dla każdej techniki badania. Następnie przeprowadzimy jednoczynnikową analizę ANOVA, aby określić, czy te różnice są istotne statystycznie.

Powiązane: Jak wykreślić wiele wykresów pudełkowych na jednym wykresie w języku R

Krok 3: Wykonaj jednokierunkową ANOVA.

Poniższy kod pokazuje, jak przeprowadzić jednoczynnikową analizę ANOVA, aby sprawdzić różnice między średnimi wynikami egzaminu w każdej grupie:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Ponieważ ogólna wartość p ( 0,0476 ) jest mniejsza niż 0,05, oznacza to, że każda grupa nie ma tego samego średniego wyniku z egzaminu. Następnie przeprowadzimy test Dunnetta, aby określić, która technika badania daje średnie wyniki egzaminów różniące się od wyników grupy kontrolnej.

Krok 4: Wykonaj test Dunnetta.

Aby wykonać test Dunnetta w R, możemy skorzystać z funkcji DunnettTest() z biblioteki DescTools , która wykorzystuje następującą składnię:

Test Dunnetta (x, g)

Złoto:

• x: wektor liczbowy wartości danych (np. wyników egzaminu)
• g: wektor określający nazwy grup (np. technika badania)

Poniższy kod pokazuje, jak używać tej funkcji w naszym przykładzie:

 #load DescTools library
library(DescTools)

#perform Dunnett's Test
DunnettTest(x=data$score, g=data$technique)

  Dunnett's test for comparing several treatments with a control:  
    95% family-wise confidence level

$control
             diff lwr.ci upr.ci pval    
new1-control 4.2 -1.6071876 10.00719 0.1787    
new2-control 6.4 0.5928124 12.20719 0.0296 *  

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1' '1.' 0.1 ' ' 1

Sposób interpretacji wyniku jest następujący:

• Średnia różnica w wynikach egzaminu pomiędzy nową techniką badania 1 a grupą kontrolną wynosi 4,2. Odpowiednia wartość p wynosi 0,1787 .
• Średnia różnica w wynikach egzaminu pomiędzy nową techniką badania 2 a grupą kontrolną wynosi 6,4. Odpowiednia wartość p wynosi 0,0296 .

Na podstawie wyników widzimy, że badanie Techniki 2 jest jedyną techniką, która daje średnie wyniki egzaminu znacząco (p = 0,0296) różniące się od wyników grupy kontrolnej.

Dodatkowe zasoby

Wprowadzenie do jednokierunkowej ANOVA
Jak wykonać jednokierunkową ANOVA w R
Jak wykonać test Tukeya w R