Jak wykonać test kruskala-wallisa w programie excel

Test Kruskala-Wallisa służy do określenia, czy istnieje statystycznie istotna różnica między medianami trzech lub więcej niezależnych grup. Uważa się, że jest to nieparametryczny odpowiednik jednokierunkowej analizy ANOVA.

W tym samouczku wyjaśniono, jak wykonać test Kruskala-Wallisa w programie Excel.

Przykład: test Kruskala-Wallisa w Excelu

Naukowcy chcą wiedzieć, czy trzy różne nawozy prowadzą do różnych poziomów wzrostu roślin. Losowo wybierają 30 różnych roślin i dzielą je na trzy grupy po 10, stosując do każdej grupy inny nawóz. Po miesiącu mierzą wysokość każdej rośliny.

Wykonaj poniższe kroki, aby wykonać test Kruskala-Wallisa w celu ustalenia, czy mediana wzrostu jest taka sama we wszystkich trzech grupach.

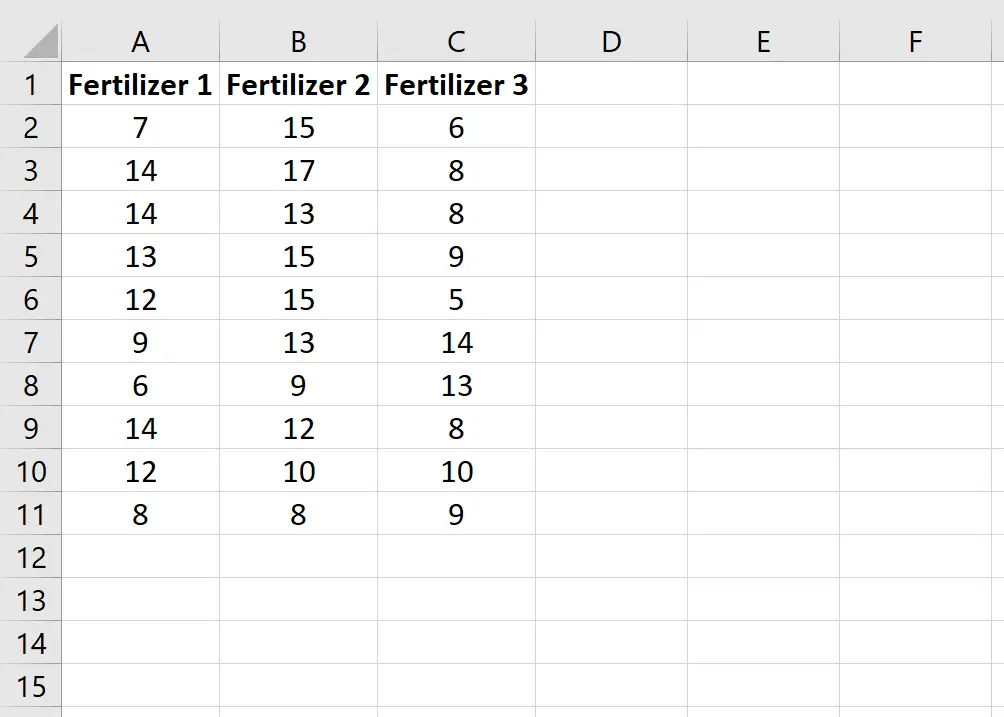
Krok 1: Wprowadź dane.

Wprowadź następujące dane, które pokazują całkowity wzrost (w calach) każdej z 10 roślin w każdej grupie:

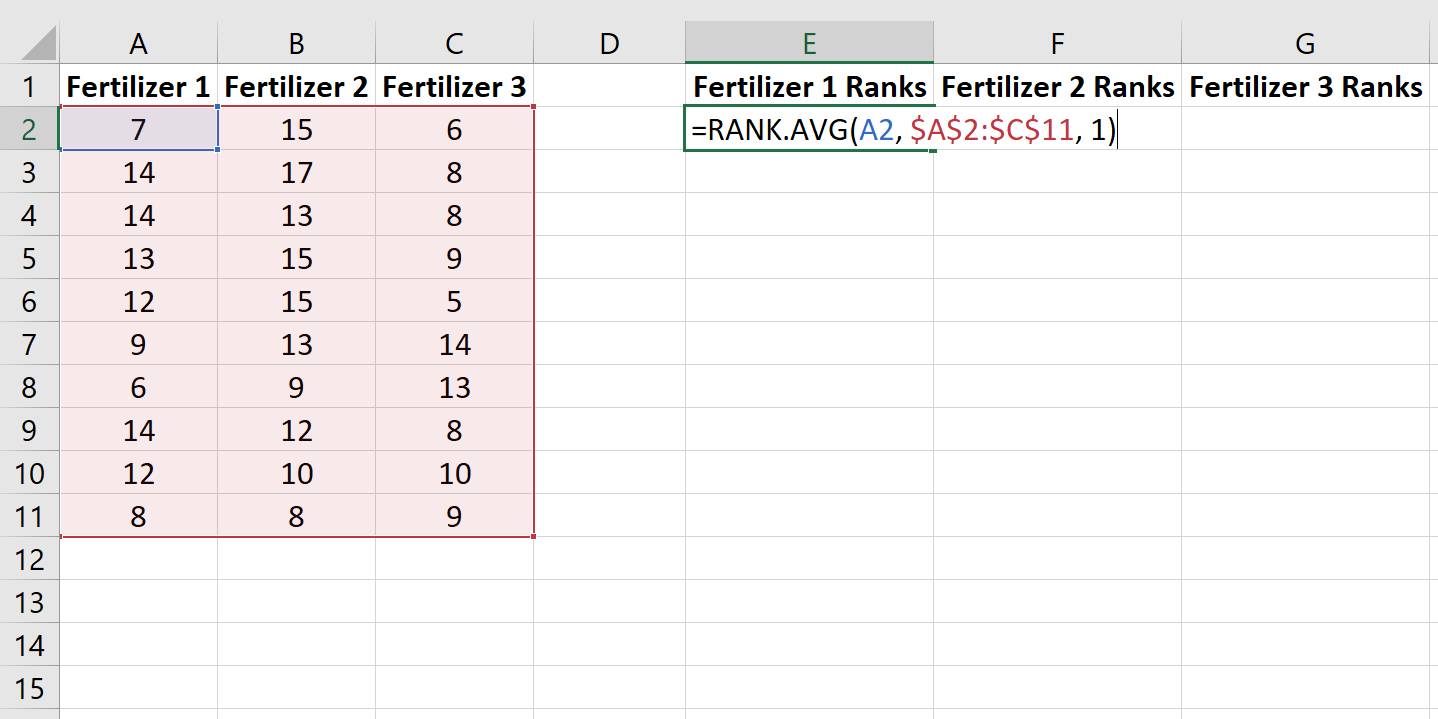
Krok 2: Sklasyfikuj dane.

Następnie użyjemy funkcji RANK.AVG() , aby przypisać rangę wzrostowi każdej rośliny spośród 30 roślin. Poniższy wzór pokazuje, jak obliczyć rangę pierwszej rośliny w pierwszej grupie:

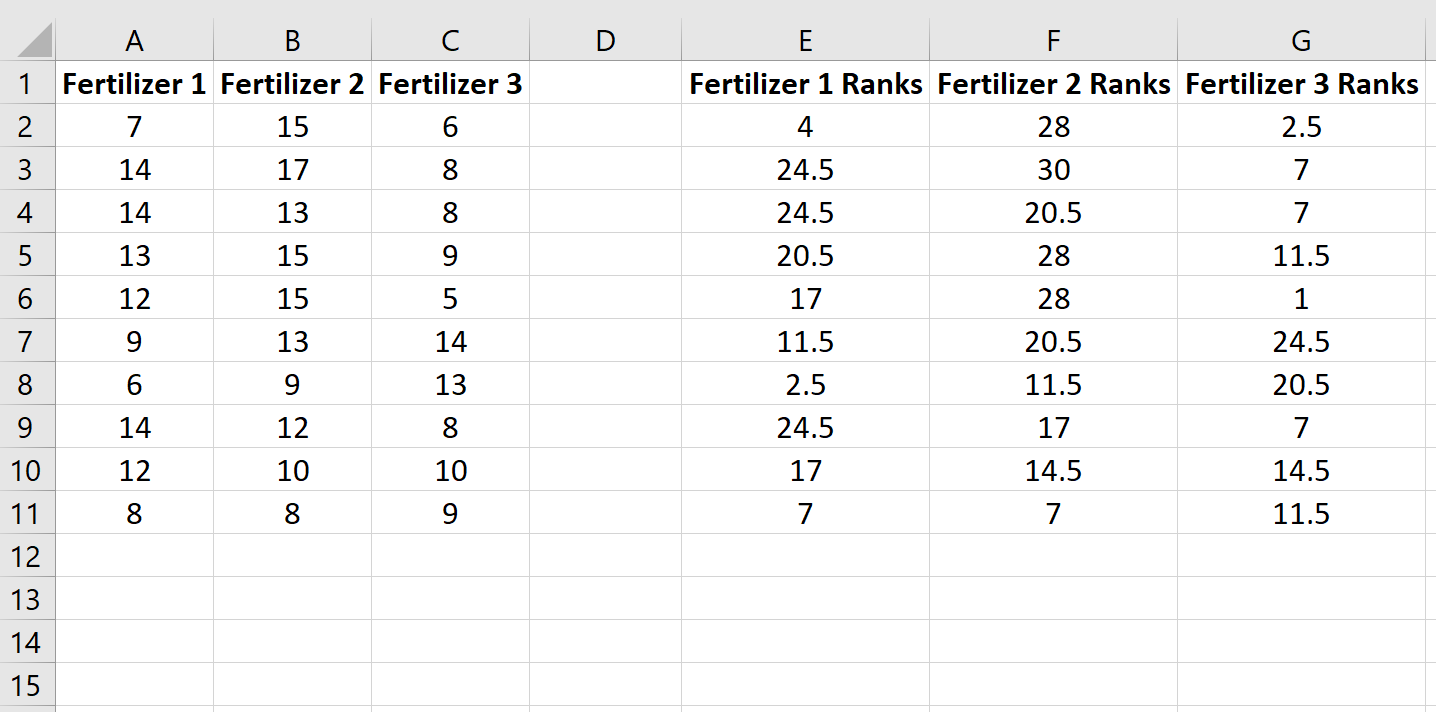
Skopiuj tę formułę do pozostałych komórek:

Następnie oblicz sumę rang dla każdej kolumny wraz z wielkością próby i kwadratową sumą rang podzieloną przez wielkość próby:

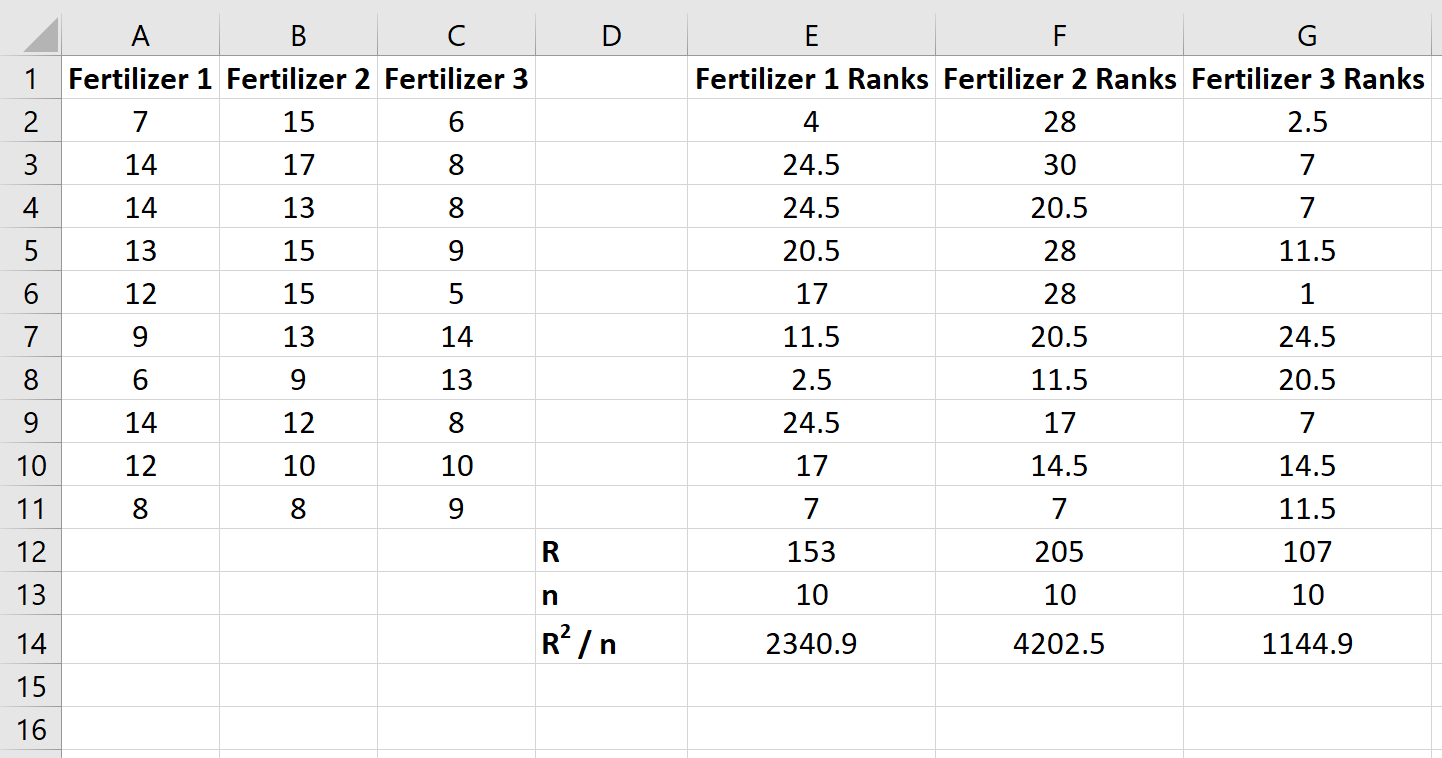
Krok 3: Oblicz statystykę testową i odpowiadającą jej wartość p.

Statystykę testową definiuje się jako:

H = 12/(n(n+1)) * ΣR _j ² /n _j – 3(n+1)

Złoto:

• n = całkowita wielkość próbki
• R _j ² = suma rang dla ^j-tej grupy
• n _j = liczebność próby ^j-tej grupy

Zgodnie z hipotezą zerową H ma rozkład chi-kwadrat z k-1 stopniami swobody.

Poniższy zrzut ekranu przedstawia wzory użyte do obliczenia statystyki testowej H i odpowiadającej jej wartości p:

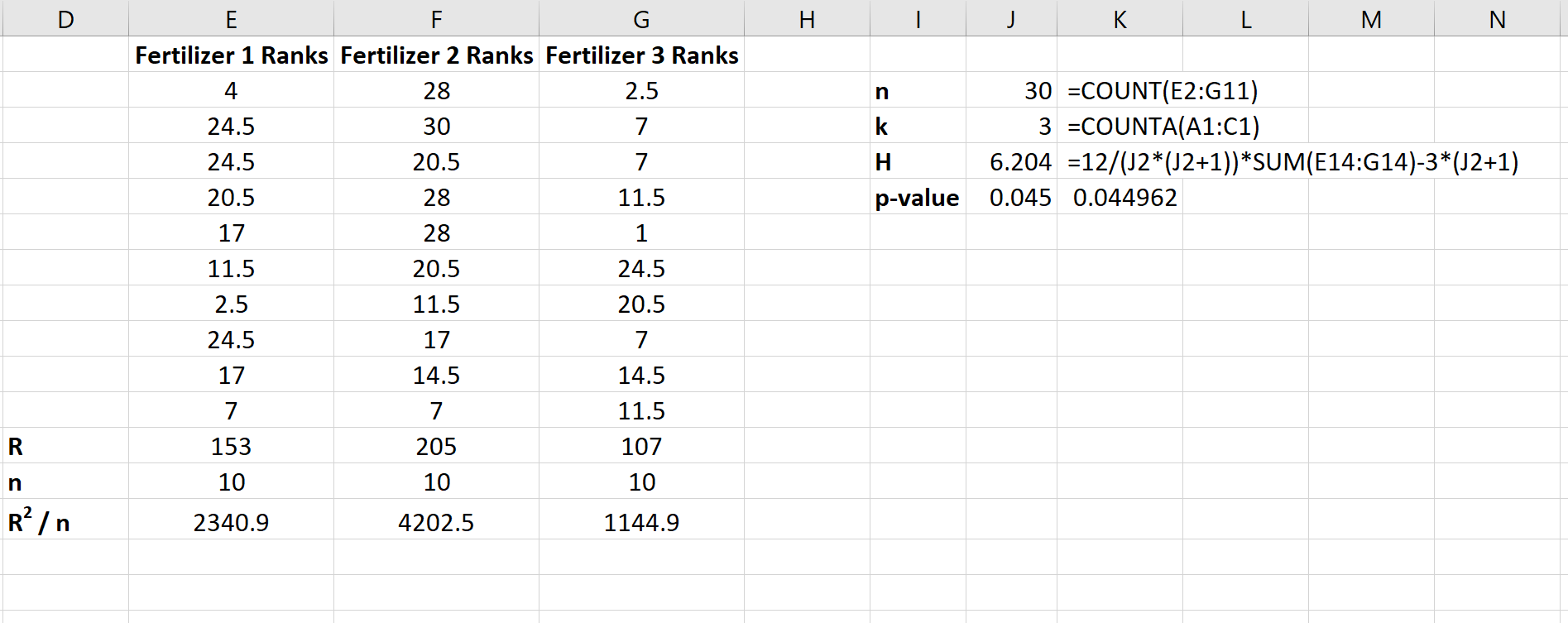
Statystyka testowa wynosi H = 6,204 , a odpowiadająca jej wartość p wynosi p = 0,045 . Ponieważ ta wartość p jest mniejsza niż 0,05, możemy odrzucić hipotezę zerową, że średni wzrost roślin jest taki sam dla wszystkich trzech nawozów. Mamy wystarczające dowody, aby stwierdzić, że rodzaj zastosowanego nawozu powoduje statystycznie istotne różnice we wzroście roślin.

Krok 4: Ogłoś wyniki.

Na koniec chcielibyśmy przedstawić wyniki testu Kruskala-Wallisa. Oto przykład, jak to zrobić:

Przeprowadzono test Kruskala-Wallista w celu ustalenia, czy średni wzrost roślin był taki sam dla trzech różnych nawozów roślinnych. Do analizy wykorzystano ogółem 30 roślin. Każdy nawóz zastosowano do 10 różnych roślin.

Test wykazał, że mediana wzrostu roślin nie była taka sama (H = 6,204, p = 0,045) pomiędzy trzema nawozami. Oznacza to, że istniała statystycznie istotna różnica w średnim wzroście roślin pomiędzy dwoma lub większą liczbą nawozów.