Test friedmana: definicja, wzór i przykład

Test Friedmana jest nieparametryczną alternatywą dla ANOVA z powtarzanymi pomiarami .

Służy do określenia, czy istnieje statystycznie istotna różnica między średnimi z trzech lub więcej grup, w których w każdej grupie występują ci sami pacjenci.

Kiedy stosować test Friedmana

Test Friedmana jest powszechnie stosowany w dwóch sytuacjach:

1. Zmierz średnie wyniki badanych w trzech lub więcej punktach czasowych.

Na przykład możesz chcieć zmierzyć pozostałe tętno uczestników na miesiąc przed rozpoczęciem programu treningowego, miesiąc po rozpoczęciu programu i dwa miesiące po zastosowaniu programu. Można wykonać test Friedmana, aby sprawdzić, czy istnieje znacząca różnica w średnim pozostałym tętnie pacjentów w tych trzech punktach czasowych.

2. Zmierz średnie wyniki przedmiotów w trzech różnych warunkach.

Na przykład możesz poprosić badanych o obejrzenie trzech różnych filmów i ocenę każdego z nich na podstawie tego, jak bardzo im się podobały. Ponieważ w każdej próbce pojawia się każdy temat, można przeprowadzić test Friedmana, aby sprawdzić, czy istnieje znacząca różnica w średniej ocenie trzech filmów.

Test Friedmana: przykład

Załóżmy, że chcemy wiedzieć, czy średni czas reakcji badanych różni się w przypadku trzech różnych leków. Aby to przetestować, rekrutujemy 10 pacjentów i mierzymy czas reakcji (w sekundach) każdego z trzech różnych leków. Wyniki dla każdego pacjenta przedstawiono poniżej:

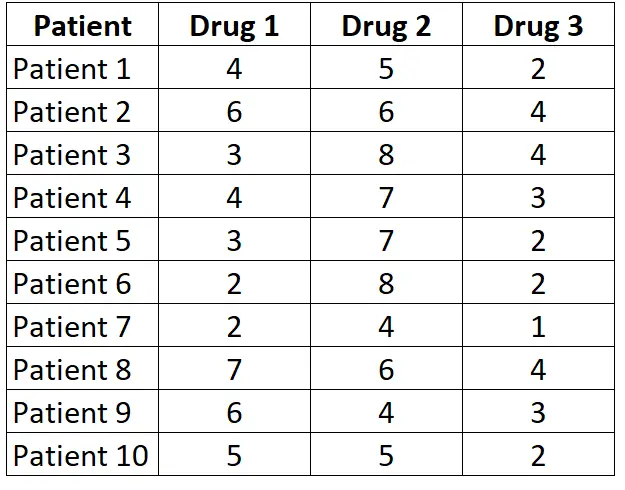
Ponieważ każdy pacjent jest mierzony na każdym z trzech leków, użyjemy testu Friedmana, aby określić, czy średni czas reakcji różni się między trzema lekami.

Krok 1. Postaw hipotezy.

Hipoteza zerowa (H ₀ ): µ ₁ = µ ₂ = µ ₃ (średnie czasy reakcji we wszystkich populacjach są równe)

Hipoteza alternatywna: (Ha): co najmniej jedna średnia populacji różni się od pozostałych

Krok 2. Wykonaj test Friedmana.

Użyjemy kalkulatora testu Friedmana, wpisując następujące dane wejściowe:

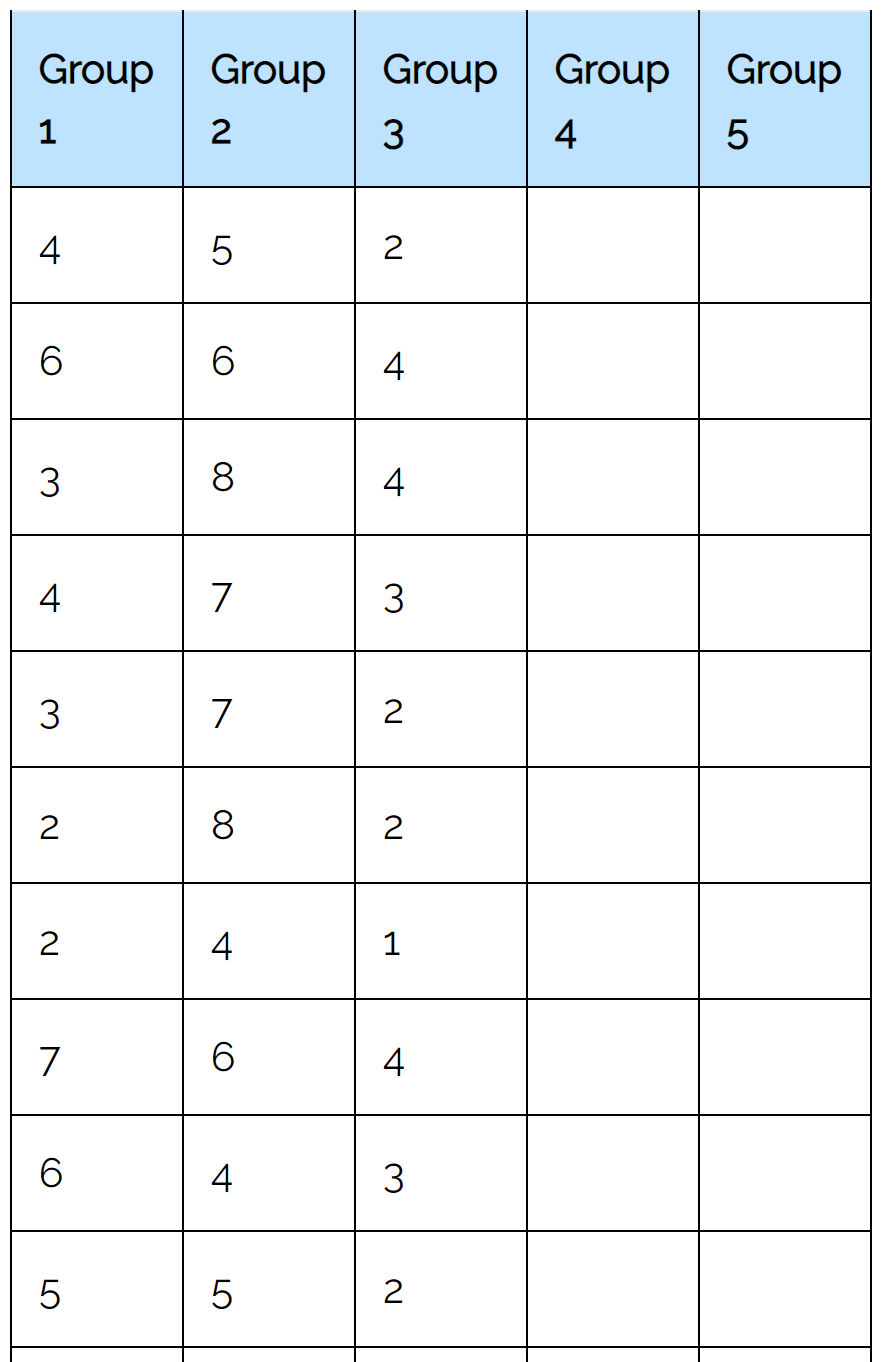
Po kliknięciu „Oblicz” automatycznie pojawi się następujący wynik:

Krok 3: Interpretacja wyników.

Statystyka testowa wynosi Q = 12,35 , a odpowiadająca jej wartość p wynosi p = 0,00208 . Ponieważ wartość ta jest mniejsza niż 0,05, możemy odrzucić hipotezę zerową, że średni czas reakcji jest taki sam dla wszystkich trzech leków.

Mamy wystarczające dowody, aby stwierdzić, że rodzaj stosowanego leku powoduje statystycznie istotne różnice w czasie reakcji.

Krok 4: Ogłoś wyniki.

Na koniec chcielibyśmy poinformować o wynikach testów. Oto przykład, jak to zrobić:

Test Friedmana przeprowadzono na 10 pacjentach, aby sprawdzić wpływ trzech różnych leków na czas odpowiedzi. Każdy pacjent stosował każdy lek jeden raz.

Wyniki wykazały, że rodzaj stosowanego leku wpływał na istotne statystycznie różnice w czasie odpowiedzi (Q = 12,35, p = 0,00208).

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak przeprowadzić test Friedmana przy użyciu różnych programów statystycznych:

Jak wykonać test Friedmana w programie Excel
Jak wykonać test Friedmana w R
Jak wykonać test Friedmana w Pythonie
Jak wykonać test Friedmana w Stata
Internetowy kalkulator testu Friedmana