Testowanie hipotez dla średniej

Przez Benjamin Anderson 3 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, na czym polega testowanie hipotez dla średniej w statystyce. W ten sposób znajdziesz wzór testu hipotezy na średnią, a dodatkowo ćwiczenie rozwiązane krok po kroku.

Na czym polega testowanie hipotez dla średniej?

Testowanie hipotez dla średniej jest metodą statystyczną stosowaną do odrzucenia lub odrzucenia hipotezy zerowej średniej populacji.

Mówiąc dokładniej, testowanie hipotezy pod kątem średniej polega na obliczeniu statystyki testowej i porównaniu jej z wartością krytyczną, aby odrzucić hipotezę zerową lub nie.

Należy zauważyć, że testy hipotez mają różne nazwy; w statystyce nazywane są one również kontrastami hipotez, testami hipotez lub testami istotności.

Testowanie hipotezy Wzór na średnią

Następnie zobaczymy, jak obliczana jest statystyka testu hipotezy dla średniej. Jednakże wzór różni się nieznacznie w zależności od tego, czy wariancja jest znana, czy nie, więc najpierw zobaczymy, jak to się robi, gdy wariancja jest znana, a następnie, gdy wariancja jest nieznana.

Ze znanym odchyleniem

Wzór hipotezy testowej dla średniej ze znaną wariancją to:

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle \frac{\sigma}{\sqrt{n}}}$

Złoto:

$Z$

jest statystyką testową hipotezy dla średniej.
$\overline{x}$

to przykładowe środki.
$\mu$

jest proponowaną wartością średnią.
$\sigma$

jest odchyleniem standardowym populacji.
$n$

to wielkość próbki.

Po obliczeniu statystyki testu hipotezy dla średniej, wynik należy zinterpretować w celu odrzucenia lub odrzucenia hipotezy zerowej:

Jeżeli test hipotezy dla średniej jest dwustronny, hipotezę zerową odrzuca się, jeśli wartość bezwzględna statystyki jest większa niż wartość krytyczna Z _α/2 .
Jeśli test hipotezy dla średniej odpowiada prawemu ogonowi, hipoteza zerowa jest odrzucana, jeśli statystyka jest większa niż wartość krytyczna Z _α .
Jeśli test hipotezy dla średniej odpowiada lewemu ogonowi, hipoteza zerowa jest odrzucana, jeśli statystyka jest mniejsza niż wartość krytyczna -Z _α .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

W tym przypadku wartości krytyczne uzyskuje się ze znormalizowanej tabeli rozkładu normalnego .

Z nieznaną różnicą

Wzór hipotezy testowej dla średniej o nieznanej wariancji wygląda następująco:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

Złoto:

$t$

jest statystyką testującą hipotezę dla średniej, która jest zdefiniowana przez rozkład t-Studenta .
$\overline{x}$

to przykładowe środki.
$\mu$

jest proponowaną wartością średnią.
$s$

jest odchyleniem standardowym próbki.
$n$

to wielkość próbki.

Tak jak poprzednio, obliczony wynik statystyki testowej należy interpretować z wartością krytyczną, aby odrzucić lub nie hipotezę zerową:

Jeżeli test hipotezy dla średniej jest dwustronny, hipotezę zerową odrzuca się, jeśli wartość bezwzględna statystyki jest większa niż wartość krytyczna t _α/2|n-1 .
Jeśli test hipotezy dla średniej odpowiada prawemu ogonowi, hipoteza zerowa zostaje odrzucona, jeśli statystyka jest większa niż wartość krytyczna t _α|n-1 .
Jeśli test hipotezy dla średniej odpowiada lewemu ogonowi, hipoteza zerowa jest odrzucana, jeśli statystyka jest mniejsza niż wartość krytyczna -t _α|n-1 .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Gdy wariancja nie jest znana, krytyczne wartości testowe uzyskuje się z tabeli rozkładu Studenta.

Przykład sprawdzania hipotez w świecie rzeczywistym dla średniej

Aby w pełni zrozumieć koncepcję testowania hipotez dla średniej populacji, poniżej możesz zobaczyć rzeczywisty przykład tego typu testowania hipotez.

Firma technologiczna twierdzi, że bateria sprzedawanego przez nią laptopa wytrzymuje 6 godzin. Sprawdzamy, czy hipoteza ta jest fałszywa, wykonując test hipotezy na poziomie istotności α = 0,05. Aby to zrobić, postanawia się kupić 20 jednostek i obserwować żywotność baterii każdego komputera (wartości wyrażone są w godzinach):

5,2 5,9 7,1 4,2 6,5
8,5 4,6 6,8 6,9 5,8
5,1 6,5 7,0 5,3 6,2
5,7 6,6 7,5 5,1 6,1

W tym przypadku hipotezy zerowe i alternatywne testu hipotezy dotyczące średniej są następujące:

$\begin{cases}H_0: \mu=6\\[2ex] H_1:\mu\neq 6 \end{cases}$

Aby określić statystykę testową, musimy najpierw obliczyć średnią próbki i odchylenie standardowe próbki:

$\overline{x}=6,13 \qquad s=1,05$

Ponieważ nie znamy wariancji populacji, aby otrzymać statystykę testową, należy zastosować wzór na sprawdzenie hipotezy dla średniej o nieznanej wariancji:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

$\displaystyle t=\frac{6,13-6}{\displaystyle \frac{1,05}{\sqrt{20}}}$

$\displaystyle t=0,68$

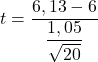
Teraz musimy znaleźć wartość krytyczną testu hipotezy, więc szukamy odpowiedniej wartości w tabeli rozkładu t-Studenta . Stopnie swobody t-Studenta są o jeden mniejsze niż liczebność próby (20-1=19), a z drugiej strony odpowiadające im prawdopodobieństwo jest o połowę mniejsze od poziomu istotności (0,05/2=0,025), ponieważ jest to testowanie hipotez.

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 19}=2,093\end{array}$

Podsumowując, ponieważ jest to test hipotezy dwustronnej i wartość bezwzględna statystyki testowej jest mniejsza niż wartość krytyczna, nie odrzuca się hipotezy zerowej, lecz odrzuca się hipotezę alternatywną.

$0,68<2,093 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

Testowanie hipotez pod kątem różnicy średnich

Test hipotezy różnicy średnich służy do odrzucenia lub przyjęcia hipotezy zerowej, że średnie w dwóch populacjach są takie same.

Zatem hipoteza zerowa testu hipotezy dla różnicy dwóch średnich jest zawsze następująca:

$H_0: \mu_1=\mu_2$

Chociaż alternatywna hipoteza może być jedną z trzech następujących:

$\begin{array}{l}H_1:\mu_1\neq \mu_2\\[2ex]H_1:\mu_1>\mu_2\\[2ex]H_1:\mu_1<\mu_2\end{array}$

Następnie wzór na obliczenie statystyki testu hipotezy dla różnicy średnich, gdy znana jest wariancja, wygląda następująco:

$\displaystyle Z=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

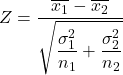
Złoto:

$Z$

jest statystyką testującą hipotezę dotyczącą różnicy dwóch średnich o znanej wariancji, która jest zgodna ze standardowym rozkładem normalnym.
$\overline{x_1}$

jest średnią próbki 1.
$\overline{x_2}$

jest średnią próbki 2.
$\sigma_1^2$

jest wariancją populacji 1.
$\sigma_2^2$

jest wariancją populacji 2.
$n_1$

to próbka o wielkości 1.
$n_2$

to próbka o wielkości 2.

Z drugiej strony wzór na obliczenie statystyki testu hipotezy dla różnicy średnich, gdy wariancja jest nieznana, jest następujący:

$\displaystyle t=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

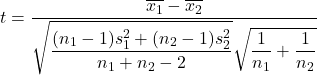
Złoto:

$t$

jest statystyką testującą hipotezę dotyczącą różnicy dwóch średnich o nieznanej wariancji, która jest zgodna z rozkładem t-Studenta.
$\overline{x_1}$

jest średnią próbki 1.
$\overline{x_2}$

jest średnią próbki 2.
$s_1^2$

jest wariancją próbki 1.
$s_2^2$

jest wariancją próbki 2.
$n_1$

to próbka o wielkości 1.
$n_2$

to próbka o wielkości 2.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej

Na czym polega testowanie hipotez dla średniej?

Testowanie hipotezy Wzór na średnią

Ze znanym odchyleniem

Z nieznaną różnicą

Przykład sprawdzania hipotez w świecie rzeczywistym dla średniej

Testowanie hipotez pod kątem różnicy średnich

o autorze

Dr Benjamin Anderson

Dodaj komentarz