Testowanie hipotez pod kątem różnicy średnich

Przez Benjamin Anderson 3 sierpnia, 2023 Statystyka 0 komentarzy

W artykule wyjaśniono, na czym polega testowanie hipotez różnicy średnich w statystyce i do czego służy. W ten sam sposób dowiesz się, jak przeprowadzić test hipotezy na temat różnicy średnich, oraz dowiesz się, jak wykonać ćwiczenie rozwiązane krok po kroku.

Na czym polega testowanie hipotez pod kątem średniej różnicy?

Testowanie hipotez pod kątem różnicy średnich to test statystyczny używany do odrzucenia lub przyjęcia hipotezy, że średnie w dwóch populacjach są różne. Oznacza to, że test hipotezy różnicy średnich służy do ustalenia, czy średnie dwóch populacji są takie same, czy różne.

Należy pamiętać, że decyzje podejmowane podczas testowania hipotez opierają się na wcześniej ustalonym poziomie ufności , dlatego nie można zagwarantować, że wynik testu hipotezy będzie zawsze prawidłowy, ale raczej, że jest to najbardziej prawdopodobny wynik, który jest prawdziwy.

Testowanie hipotez pod kątem różnicy dwóch średnich polega na obliczeniu statystyki testowej i porównaniu jej z wartością krytyczną, aby odrzucić hipotezę zerową lub nie. Poniżej zobaczymy, jak przeprowadzić test hipotezy dla różnicy średnich.

Na koniec pamiętaj, że w statystyce testowanie hipotez można również nazwać kontrastami hipotez, testowaniem hipotez lub testowaniem istotności.

➤ Zobacz: Próbkowanie rozkładu różnicy średnich

Testowanie hipotez Wzór na różnicę średnich

Wzór, którego należy używać do testowania hipotez dotyczących różnicy średnich, różni się w zależności od tego, czy znane są wariancje populacji, a jeśli nie, to czy można założyć, że są takie same lub różne. Zatem w tej sekcji zobaczymy, jakiej formuły użyć w zależności od przypadku.

Znane odmiany

Wzór na obliczenie statystyki testu hipotezy dla różnicy średnich, gdy znane są wariancje, jest następujący:

$\displaystyle Z=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Złoto:

$Z$

jest statystyką testującą hipotezę dotyczącą różnicy dwóch średnich o znanej wariancji, która jest zgodna ze standardowym rozkładem normalnym.
$\mu_1$

jest średnią populacji 1.
$\mu_2$

jest średnią populacji 2.
$\overline{x_1}$

jest średnią próbki 1.
$\overline{x_2}$

jest średnią próbki 2.
$\sigma_1$

jest odchyleniem standardowym populacji 1.
$\sigma_2$

jest odchyleniem standardowym populacji 2.
$n_1$

to próbka o wielkości 1.
$n_2$

to próbka o wielkości 2.

Należy pamiętać, że jest to najrzadziej spotykany przypadek, więc tej formuły używa się tylko w niektórych określonych przypadkach.

Nieznane i równe odchylenia

Wzór na obliczenie statystyki testu hipotezy dla różnicy średnich, gdy wariancje populacji są nieznane, ale zakłada się, że są równe :

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Złoto:

$t$

jest statystyką testującą hipotezę dotyczącą różnicy średnich o nieznanych wariancjach, która jest zgodna z rozkładem t-Studenta z n ₁ + n ₂ -2 stopniami swobody.
$\mu_1$

jest średnią populacji 1.
$\mu_2$

jest średnią populacji 2.
$\overline{x_1}$

jest średnią próbki 1.
$\overline{x_2}$

jest średnią próbki 2.
$s_p$

jest połączonym odchyleniem standardowym.
$n_1$

to próbka o wielkości 1.
$n_2$

to próbka o wielkości 2.

Łączne odchylenie standardowe dwóch próbek oblicza się za pomocą następującego wzoru:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

Nieznane i różne odmiany

Jeżeli wariancje populacji nie są znane, a ponadto zakłada się, że są różne, wzór na obliczenie statystyki testu hipotezy dla różnicy średnich jest następujący:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

Złoto:

$t$

jest statystyką testującą hipotezę dotyczącą różnicy średnich o nieznanych wariancjach, która jest zgodna z rozkładem t-Studenta.
$\mu_1$

jest średnią populacji 1.
$\mu_2$

jest średnią populacji 2.
$\overline{x_1}$

jest średnią próbki 1.
$\overline{x_2}$

jest średnią próbki 2.
$\sigma_1$

jest odchyleniem standardowym populacji 1.
$\sigma_2$

jest odchyleniem standardowym populacji 2.
$n_1$

to próbka o wielkości 1.
$n_2$

to próbka o wielkości 2.

Jednakże w tym przypadku stopnie swobody rozkładu t-Studenta obliczane są ze wzoru:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ Zobacz: Wzór na przedział ufności dla różnicy średnich

Konkretny przykład testowania hipotezy pod kątem różnicy średnich

Aby zakończyć przyswajanie koncepcji testowania hipotez na podstawie różnicy średnich, zobaczymy konkretny przykład tego typu testowania hipotez.

Chcesz przeprowadzić badanie statystyczne dotyczące wynagrodzeń w dwóch konkurencyjnych firmach, a dokładniej chcesz ustalić, czy średnie wynagrodzenie w obu firmach jest różne. W tym celu pobiera się próbę 47 pracowników z jednego przedsiębiorstwa i drugą próbę 55 pracowników z drugiego przedsiębiorstwa. Z pierwszej próby uzyskano średnie wynagrodzenie w wysokości 40 000 USD i odchylenie standardowe w wysokości 12 000 USD, natomiast w drugiej próbie uzyskano średnie wynagrodzenie w wysokości 46 000 USD i odchylenie standardowe w wysokości 18 000 USD. Wykonaj test hipotezy z poziomem istotności 5%, aby określić, czy średnie wynagrodzenia różnią się, czy nie.

W tym przypadku hipoteza zerowa i hipoteza alternatywna testu hipotezy dla różnicy dwóch średnich są następujące:

$\begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}$

W tym przypadku luki populacyjne nie są znane, ale można założyć, że są równe, gdyż są to firmy konkurencyjne, a warunki pracy na rynku, na którym działają, są bardzo podobne. Zatem wzór na statystykę testującą hipotezę dotyczącą różnicy średnich, którą powinniśmy zastosować, wygląda następująco:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Dlatego obliczamy zbiorcze odchylenie standardowe dwóch próbek:

$\begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}$

Zastosujemy teraz wzór na testowanie hipotezy dla różnicy średnich:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}=\cfrac{(40000-46000)-0}{\displaystyle 15530,61\sqrt{\frac{1}{47}+\frac{1}{55}}}=-1,94$

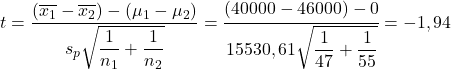
Natomiast wartości krytycznej testu hipotezy dla różnicy średnich szukamy w tabeli t-Studenta :

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}$

Następnie, ponieważ wartość bezwzględna statystyki testowej jest mniejsza niż krytyczna wartość testowa, przyjmuje się hipotezę zerową, a hipotezę alternatywną odrzuca się.

$|-1,94|=1,94<1,984 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej

Na czym polega testowanie hipotez pod kątem średniej różnicy?

Testowanie hipotez Wzór na różnicę średnich

Znane odmiany

Nieznane i równe odchylenia

Nieznane i różne odmiany

Konkretny przykład testowania hipotezy pod kątem różnicy średnich

o autorze

Dr Benjamin Anderson

Dodaj komentarz