Jak wykonać test t korelacji

Współczynnik korelacji Pearsona służy do ilościowego określenia liniowego powiązania między dwiema zmiennymi.

Zawsze przyjmuje wartość z zakresu od -1 do 1, gdzie:

• -1 oznacza doskonale ujemną korelację liniową.
• Wartość 0 oznacza brak korelacji liniowej.
• 1 wskazuje doskonale dodatnią korelację liniową.

Aby określić, czy współczynnik korelacji jest istotny statystycznie, można wykonać test t, który obejmuje obliczenie wyniku t i odpowiadającej mu wartości p.

Wzór na obliczenie wyniku t jest następujący:

t = r√ (n-2) / (1-r ² )

Złoto:

• r: Współczynnik korelacji
• n: Wielkość próbki

Wartość p oblicza się jako odpowiadającą dwustronną wartość p dla rozkładu t z n-2 stopniami swobody.

Poniższy przykład pokazuje, jak wykonać test t dla współczynnika korelacji.

Przykład: Przeprowadzanie testu t dla korelacji

Załóżmy, że mamy następujący zestaw danych z dwiema zmiennymi:

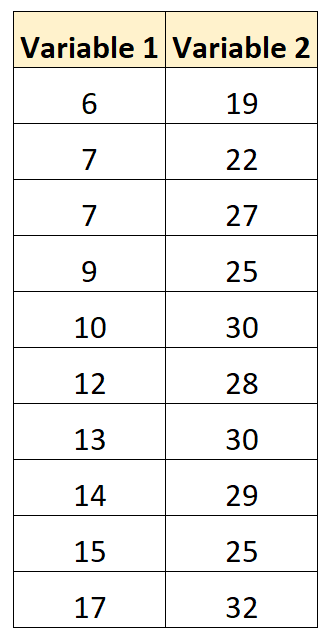
Używając oprogramowania statystycznego (Excel, R, Python itp.), możemy obliczyć współczynnik korelacji między dwiema zmiennymi na 0,707 .

Jest to bardzo dodatnia korelacja, ale aby określić, czy jest istotna statystycznie, musimy obliczyć odpowiedni wynik t i wartość p.

Wynik t możemy obliczyć w następujący sposób:

• t = r√ (n-2) / (1-r ² )
• t = 0,707√ (10-2) / (1-0,707 ² )
• t = 2,828

Korzystając z kalkulatora wartości P, T-score , stwierdzamy, że odpowiadająca wartość p wynosi 0,022 .

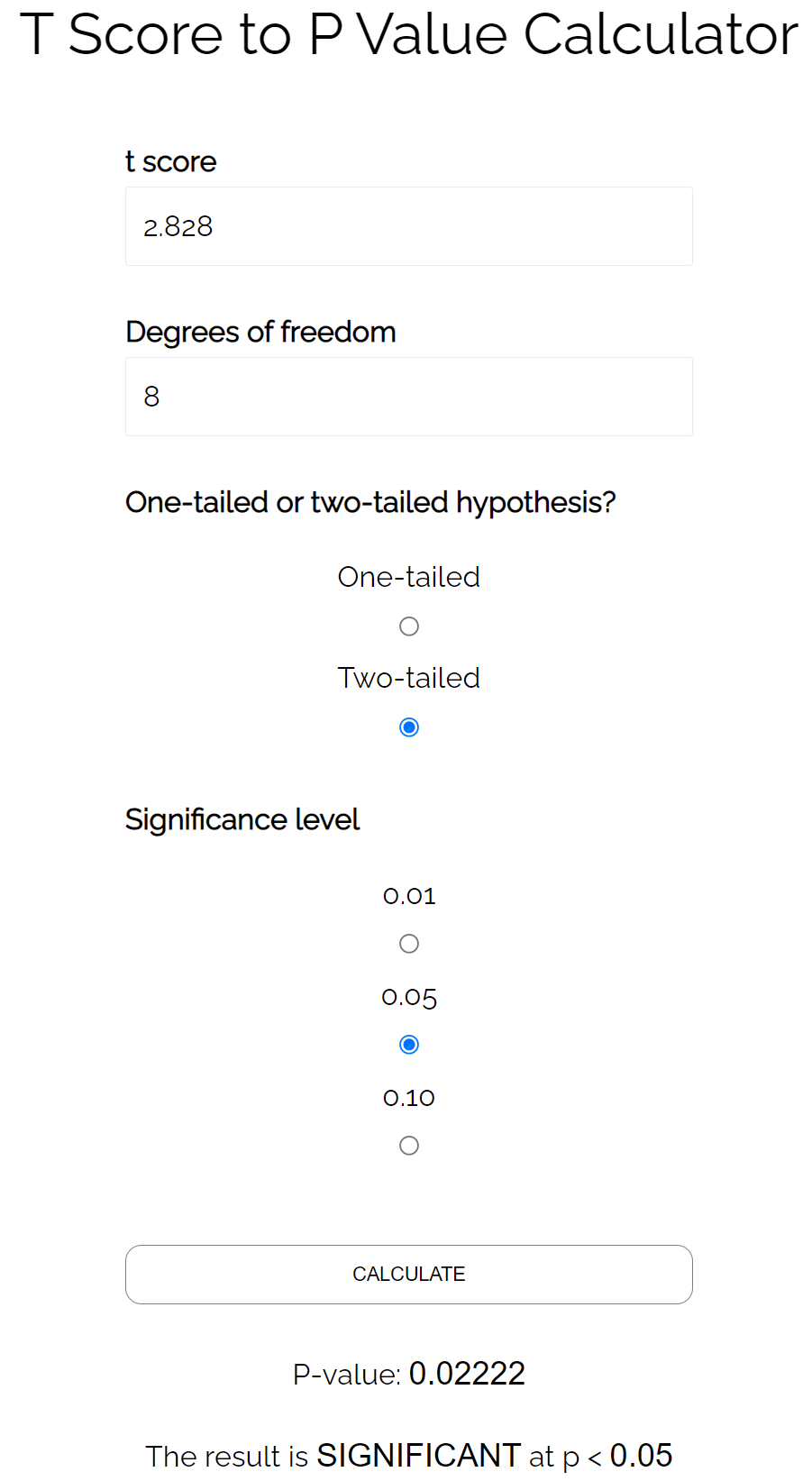
Ponieważ ta wartość p jest mniejsza niż 0,05, można wyciągnąć wniosek, że korelacja między tymi dwiema zmiennymi jest istotna statystycznie.

Dodatkowe zasoby

Jak wykonać test korelacji w programie Excel
Jak wykonać test korelacji w R
Co uważa się za „słabą” korelację?
Co uważa się za „silną” korelację?