Jak wykonać test korelacji w r (z przykładami)

Jednym ze sposobów ilościowego określenia związku między dwiema zmiennymi jest użycie współczynnika korelacji Pearsona , który jest miarą liniowego związku między dwiema zmiennymi .

Zawsze przyjmuje wartość z zakresu od -1 do 1, gdzie:

• -1 oznacza całkowicie ujemną korelację liniową pomiędzy dwiema zmiennymi
• Wartość 0 oznacza brak liniowej korelacji pomiędzy dwiema zmiennymi
• 1 wskazuje doskonale dodatnią korelację liniową pomiędzy dwiema zmiennymi

Aby określić, czy współczynnik korelacji jest istotny statystycznie, można obliczyć odpowiedni wynik t i wartość p.

Wzór na obliczenie wyniku t współczynnika korelacji (r) jest następujący:

t = r * √ n-2 / √ 1-r ²

Wartość p oblicza się jako odpowiadającą dwustronną wartość p dla rozkładu t z n-2 stopniami swobody.

Przykład: test korelacji w R

Aby określić, czy współczynnik korelacji między dwiema zmiennymi jest istotny statystycznie, można wykonać test korelacji w języku R, stosując następującą składnię:

cor.test(x, y, method=c(“pearson”, “kendall”, “włócznik”))

Złoto:

• x, y: cyfrowe wektory danych.
• metoda: Metoda stosowana do obliczenia korelacji między dwoma wektorami. Wartość domyślna to „Pearson”.

Załóżmy na przykład, że w R mamy następujące dwa wektory:

 x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23)
y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)

Przed wykonaniem testu korelacji między dwiema zmiennymi możemy stworzyć szybki wykres rozrzutu, aby zwizualizować ich związek:

 #create scatterplot
plot(x, y, pch= 16 )

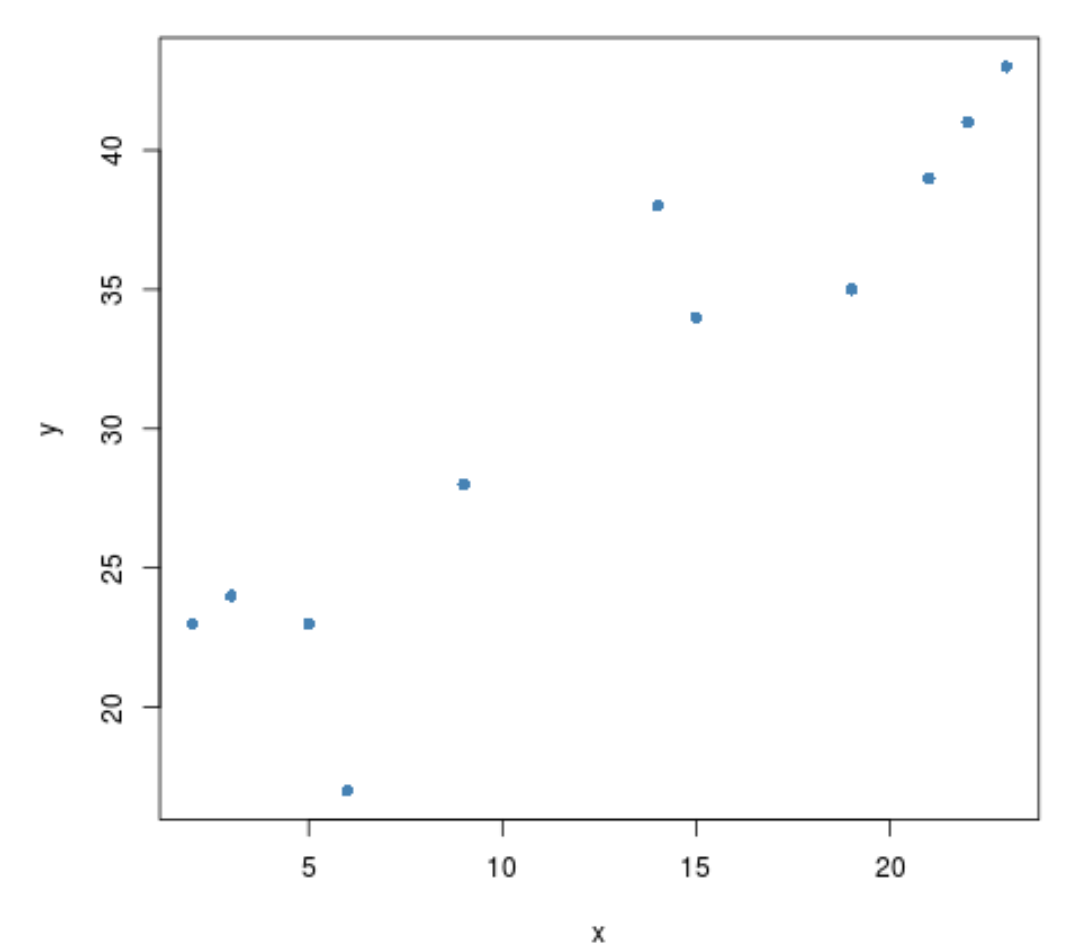
Wydaje się, że istnieje dodatnia korelacja między obiema zmiennymi. Oznacza to, że gdy jedno wzrasta, drugie również ma tendencję do zwiększania się.

Aby sprawdzić, czy ta korelacja jest istotna statystycznie, możemy wykonać test korelacji:

 #perform correlation test between the two vectors
cor.test(x, y)

	Pearson's product-moment correlation

data: x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7575203 0.9799783
sample estimates:
      horn 
0.9279869

Współczynnik korelacji pomiędzy obydwoma wektorami wynosi 0,9279869 .

Statystyka testowa wynosi 7,8756 , a odpowiadająca jej wartość p wynosi 1,35e-05 .

Ponieważ wartość ta jest mniejsza niż 0,05, mamy wystarczające dowody, aby stwierdzić, że korelacja między obiema zmiennymi jest istotna statystycznie.

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat współczynników korelacji:

Wprowadzenie do współczynnika korelacji Pearsona
Co uważa się za „silną” korelację?
Pięć hipotez korelacji Pearsona