Jak wykonać test kruskala-wallisa w spss

Test Kruskala -Wallisa służy do określenia, czy istnieje statystycznie istotna różnica między medianami trzech lub więcej niezależnych grup. Uważa się, że jest to nieparametryczny odpowiednik jednokierunkowej analizy wariancji ANOVA .

W tym samouczku wyjaśniono, jak wykonać test Kruskala-Wallisa w SPSS.

Przykład: test Kruskala-Wallisa w SPSS

Badacz chce wiedzieć, czy trzy leki mają różny wpływ na ból kolana. Rekrutuje więc 30 osób, u których wszystkie odczuwają podobny ból kolana, i losowo dzieli je na trzy grupy, aby otrzymały lek 1, lek 2 lub lek 3.

Po miesiącu przyjmowania leku badacz prosi każdą osobę o ocenę bólu kolana w skali od 1 do 100, gdzie 100 oznacza ból najcięższy. Poniżej prezentujemy wyniki 30 osób:

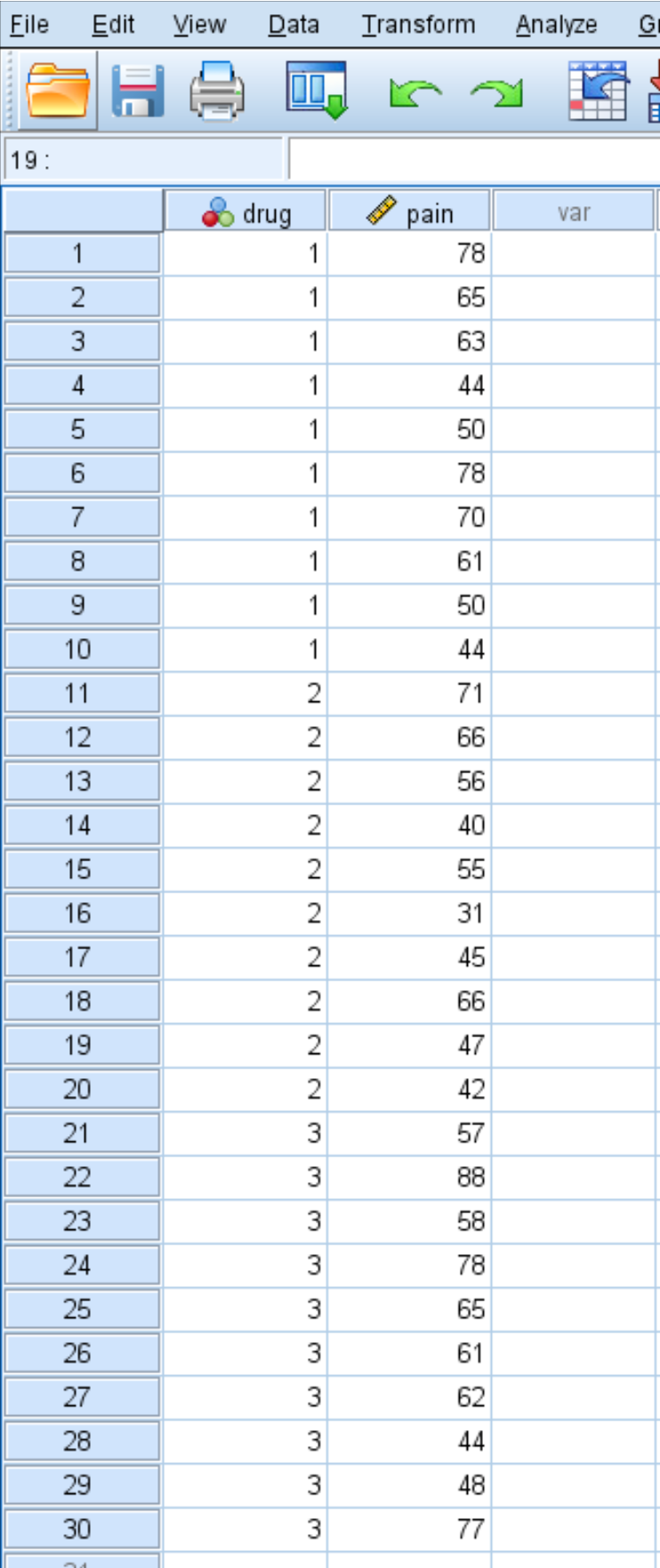
Wykonaj następujące kroki, aby wykonać test Kruskala-Wallisa w celu ustalenia, czy istnieje różnica w zgłaszanym poziomie bólu kolana pomiędzy trzema grupami:

Krok 1: Wykonaj test Kruskala-Wallisa.

Kliknij kartę Analiza , następnie Testy nieparametryczne , następnie Starsze okna dialogowe , a następnie K niezależnych próbek :

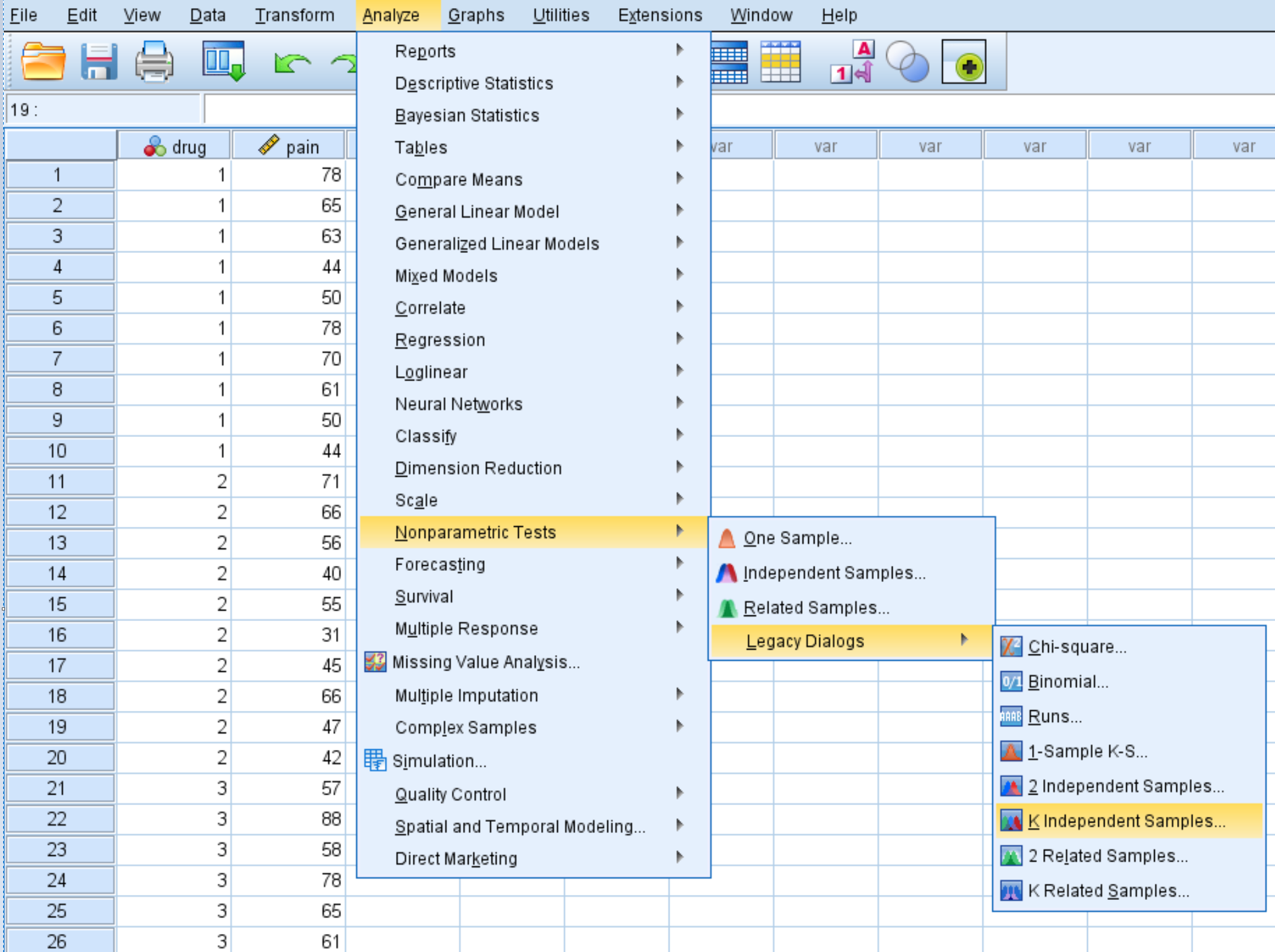
W wyświetlonym oknie przeciągnij zmienną ból do pola o nazwie Lista zmiennych testowych i lek do pola o nazwie Zmienna grupująca. Następnie kliknij Ustaw zakres i ustaw wartość minimalną na 1, a maksymalną na 3. Następnie kliknij Kontynuuj . Upewnij się, że pole obok Kruskal-Wallis H jest zaznaczone, a następnie kliknij OK .

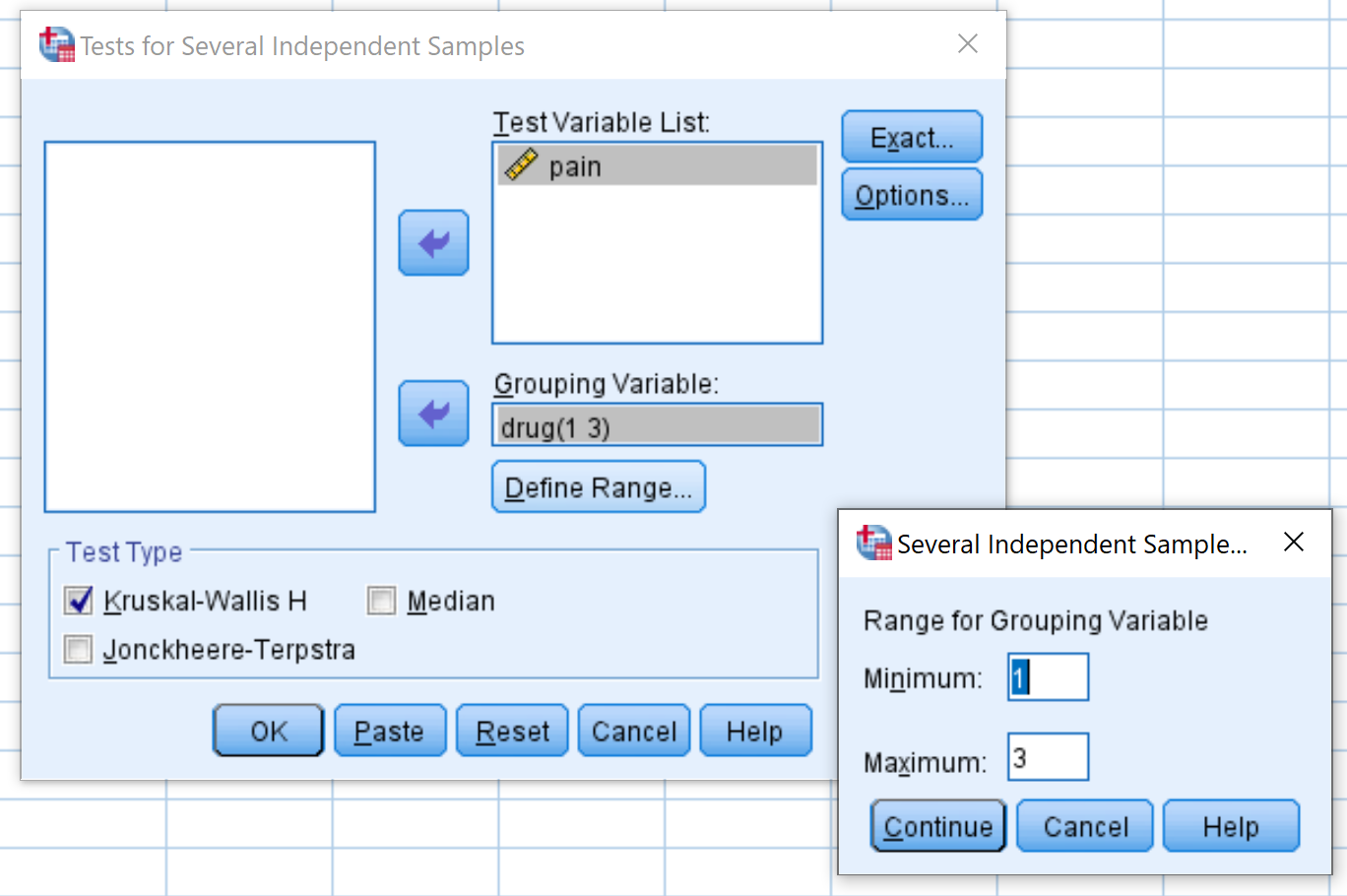
Krok 2: Interpretacja wyników.

Po kliknięciu OK pojawią się wyniki testu Kruskala-Wallisa:

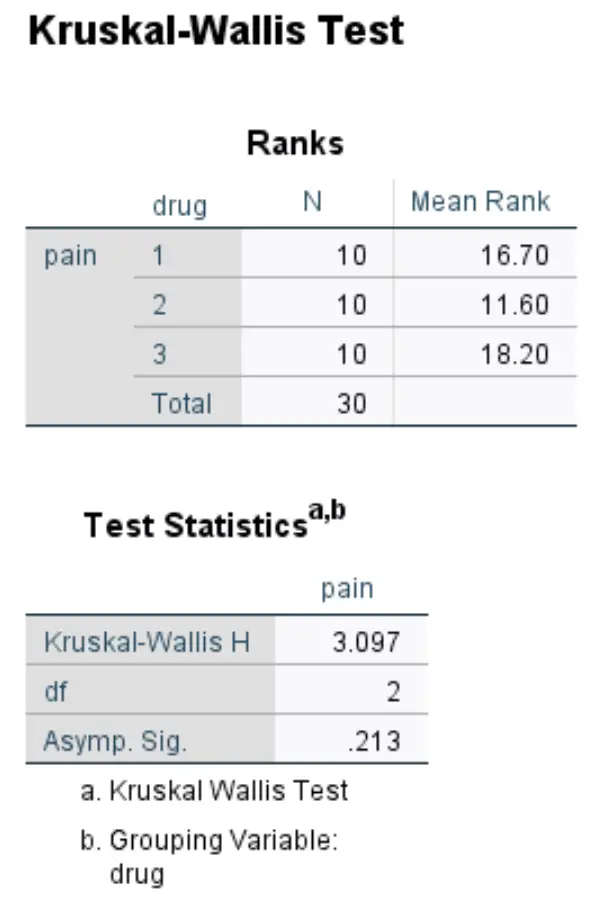
Druga tabela w wynikach wyświetla wyniki testu:

• Kruskal-Wallis H: To jest statystyka testowa ^X2 .
• df: Są to stopnie swobody obliczone jako #groups-1 = 3-1 = 2.
• Asymp. Sig: Jest to wartość p powiązana ze statystyką testową X ² wynoszącą 3,097 z 2 stopniami swobody. Można to również znaleźć za pomocą kalkulatora wyniku chi-kwadrat do wartości P.

Ponieważ wartość p (0,213) jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej. Nie mamy wystarczających dowodów, aby stwierdzić, że istnieje statystycznie istotna różnica w ocenie bólu kolana pomiędzy tymi trzema grupami.