Jak wykonać test niezależności chi-kwadrat w programie excel

Test niezależności chi-kwadrat służy do określenia, czy istnieje istotny związek między dwiema zmiennymi kategorycznymi.

W tym samouczku wyjaśniono, jak wykonać test niezależności chi-kwadrat w programie Excel.

Przykład: Test niezależności chi-kwadrat w programie Excel

Załóżmy, że chcemy wiedzieć, czy płeć jest powiązana z preferencją partii politycznej. Bierzemy prostą losową próbę 500 wyborców i pytamy ich o preferencje dotyczące partii politycznych. Wyniki badania prezentuje poniższa tabela:

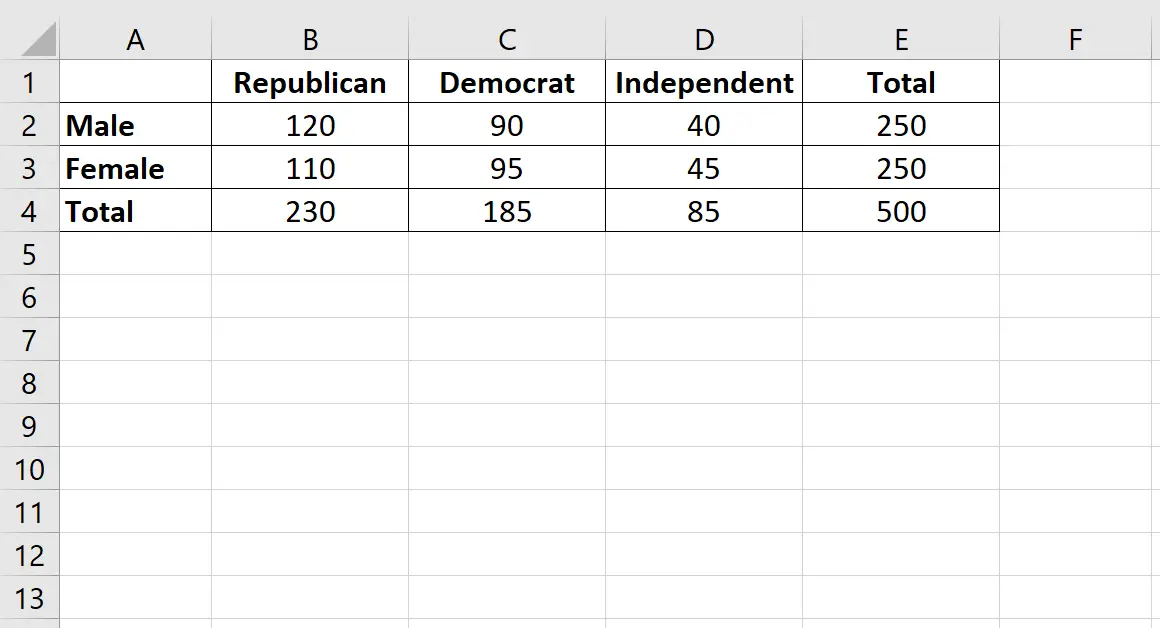
Wykonaj poniższe kroki, aby przeprowadzić test niezależności chi-kwadrat w celu ustalenia, czy płeć jest powiązana z preferencjami partii politycznych.

Krok 1: Zdefiniuj założenia.

Test niezależności Chi-kwadrat przeprowadzimy przy następujących założeniach:

• H ₀ : Preferencje dotyczące płci i partii politycznych są niezależne.
• H ₁ : Płeć i preferencje partii politycznych nie są niezależne.

Krok 2: Oblicz oczekiwane wartości.

Następnie obliczymy oczekiwane wartości dla każdej komórki w tabeli kontyngencji, korzystając z następującego wzoru:

Oczekiwana wartość = (suma wierszy * suma kolumn) / suma tabeli.

Na przykład oczekiwana wartość dla mężczyzn z Partii Republikańskiej wynosi: (230*250) / 500 = 115 .

Możemy powtórzyć tę formułę, aby uzyskać oczekiwaną wartość dla każdej komórki tabeli:

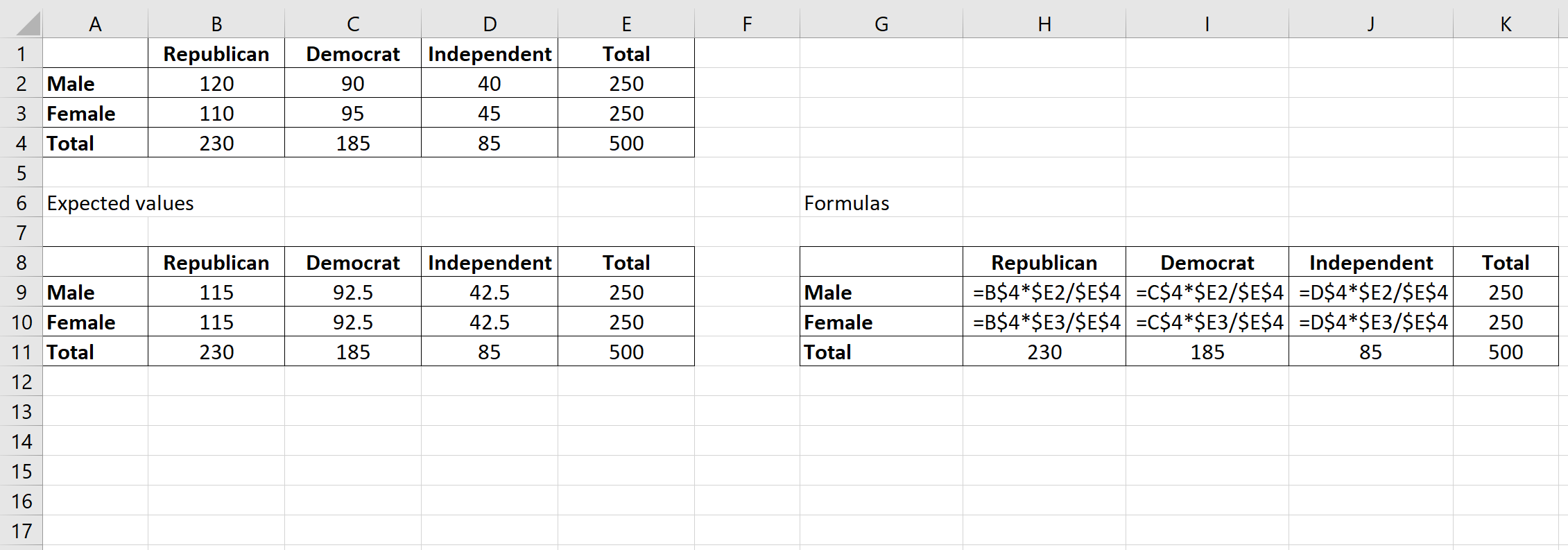
Krok 3: Oblicz (OE) ² /E dla każdej komórki w tabeli.

Następnie obliczymy (OE) ² /E dla każdej komórki w tabeli, gdzie:

• O: obserwowana wartość
• E: wartość oczekiwana

Na przykład liczba Republikanów płci męskiej miałaby wartość: (120-115) ² /115 = 0,2174 .

Możemy powtórzyć tę formułę dla każdej komórki w tabeli:

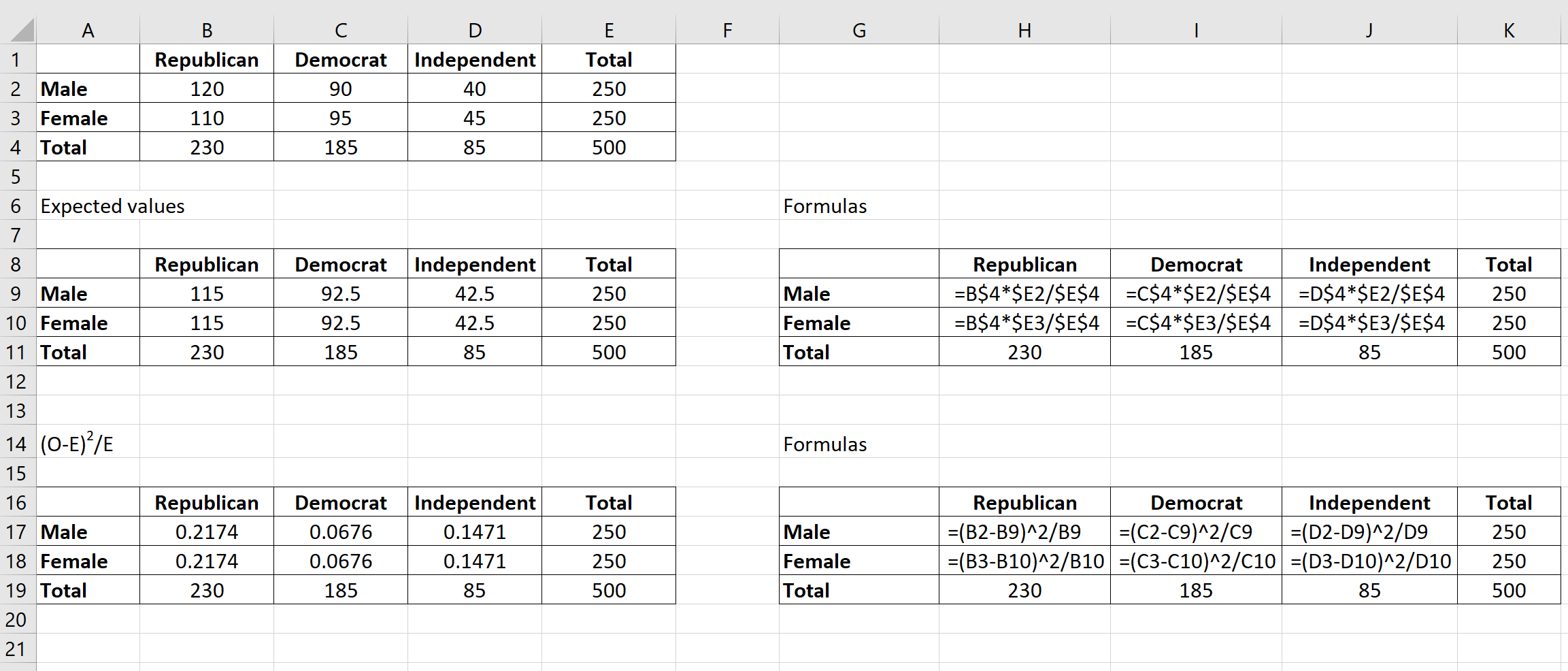
Krok 4: Oblicz statystykę testową ^X2 i odpowiadającą jej wartość p.

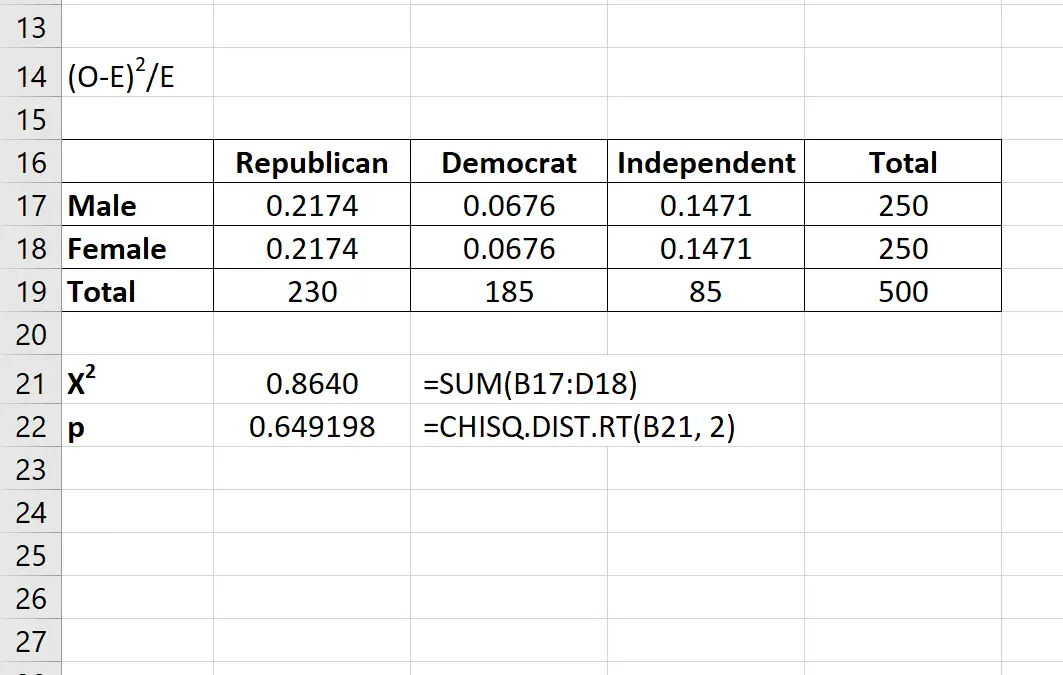
Statystyka testowa ^X2 to po prostu suma wartości z ostatniej tabeli.

Wartość p odpowiadającą statystyce testowej X ² można znaleźć za pomocą wzoru:

= ROZKŁ.CHISQ.RT(x, stopień_swobody)

Złoto:

• x: ^statystyka testowa
• deg_freedom: stopnie swobody obliczane w następujący sposób: (#rows-1) * (#columns-1)

Statystyka testowa ^X2 okazuje się wynosić 0,8640 , a odpowiadająca jej wartość p wynosi 0,649198 .

Krok 5: Wyciągnij wnioski.

Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej. Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że istnieje związek między płcią a preferencjami partii politycznych.

Uwaga: Możesz także wykonać cały test, korzystając z kalkulatora testu niezależności chi-kwadrat .