Jak przetestować normalność w r (4 metody)

Wiele testów statystycznych zakłada , że zbiory danych mają rozkład normalny.

Istnieją cztery typowe sposoby sprawdzenia tego założenia w R:

1. (Metoda wizualna) Utwórz histogram.

• Jeżeli histogram ma w przybliżeniu kształt dzwonu, zakłada się, że dane mają rozkład normalny.

2. (Metoda wizualna) Utwórz wykres QQ.

• Jeżeli punkty na wykresie leżą w przybliżeniu na prostej ukośnej, wówczas zakłada się, że dane mają rozkład normalny.

3. (Formalny test statystyczny) Wykonaj test Shapiro-Wilka.

• Jeżeli wartość p testu jest większa niż α = 0,05, wówczas zakłada się, że dane mają rozkład normalny.

4. (Formalny test statystyczny) Wykonaj test Kołmogorowa-Smirnowa.

• Jeżeli wartość p testu jest większa niż α = 0,05, wówczas zakłada się, że dane mają rozkład normalny.

Poniższe przykłady pokazują, jak zastosować każdą z tych metod w praktyce.

Metoda 1: Utwórz histogram

Poniższy kod pokazuje, jak utworzyć histogram dla zbioru danych o rozkładzie normalnym i o rozkładzie normalnym w R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ') 

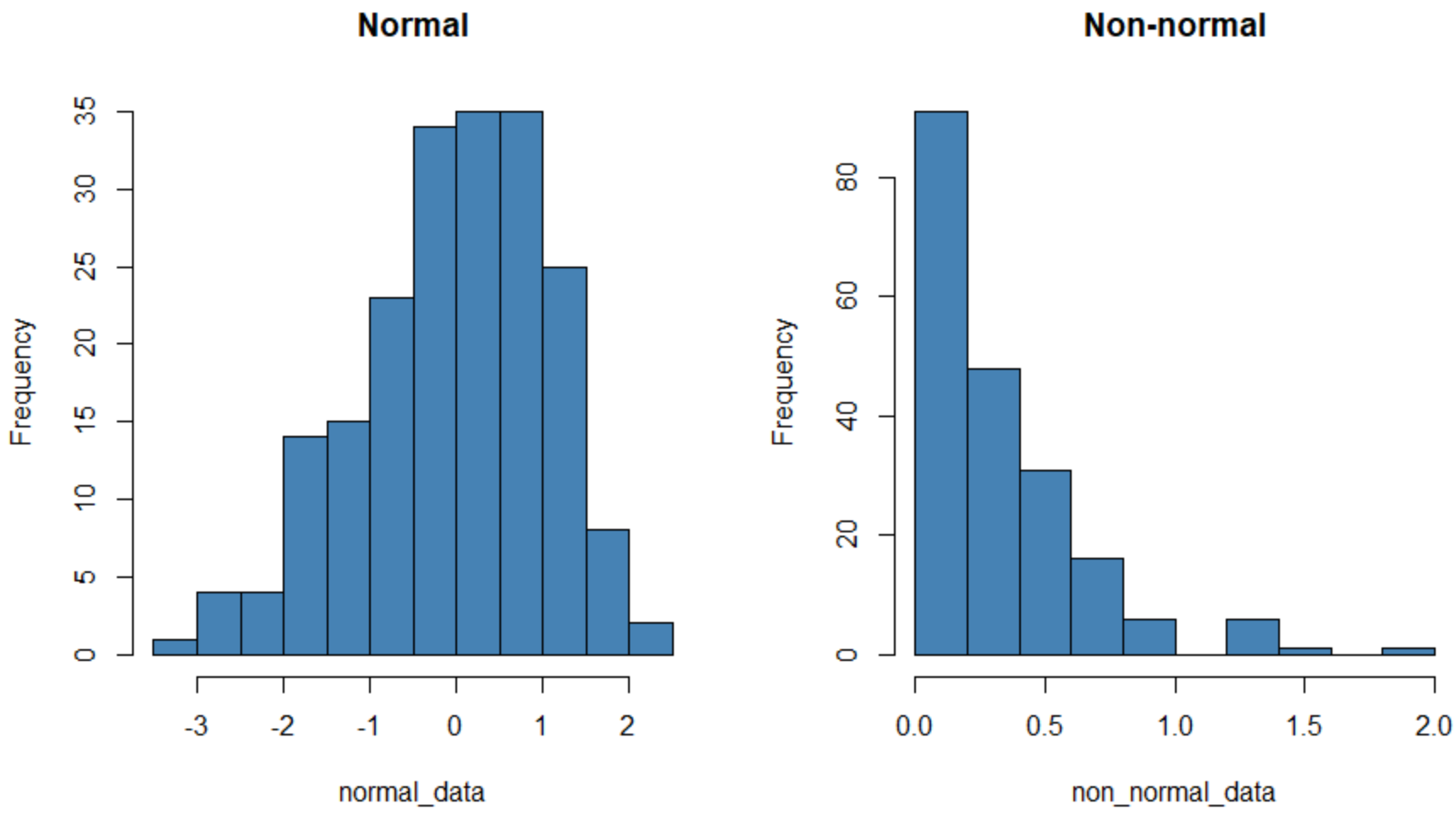
Histogram po lewej stronie przedstawia zbiór danych o rozkładzie normalnym (mniej więcej w kształcie dzwonu), a histogram po prawej stronie przedstawia zbiór danych o rozkładzie normalnym.

Metoda 2: Utwórz wykres QQ

Poniższy kod pokazuje, jak utworzyć wykres QQ dla zbioru danych o rozkładzie normalnym i o rozkładzie normalnym w R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)

qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)

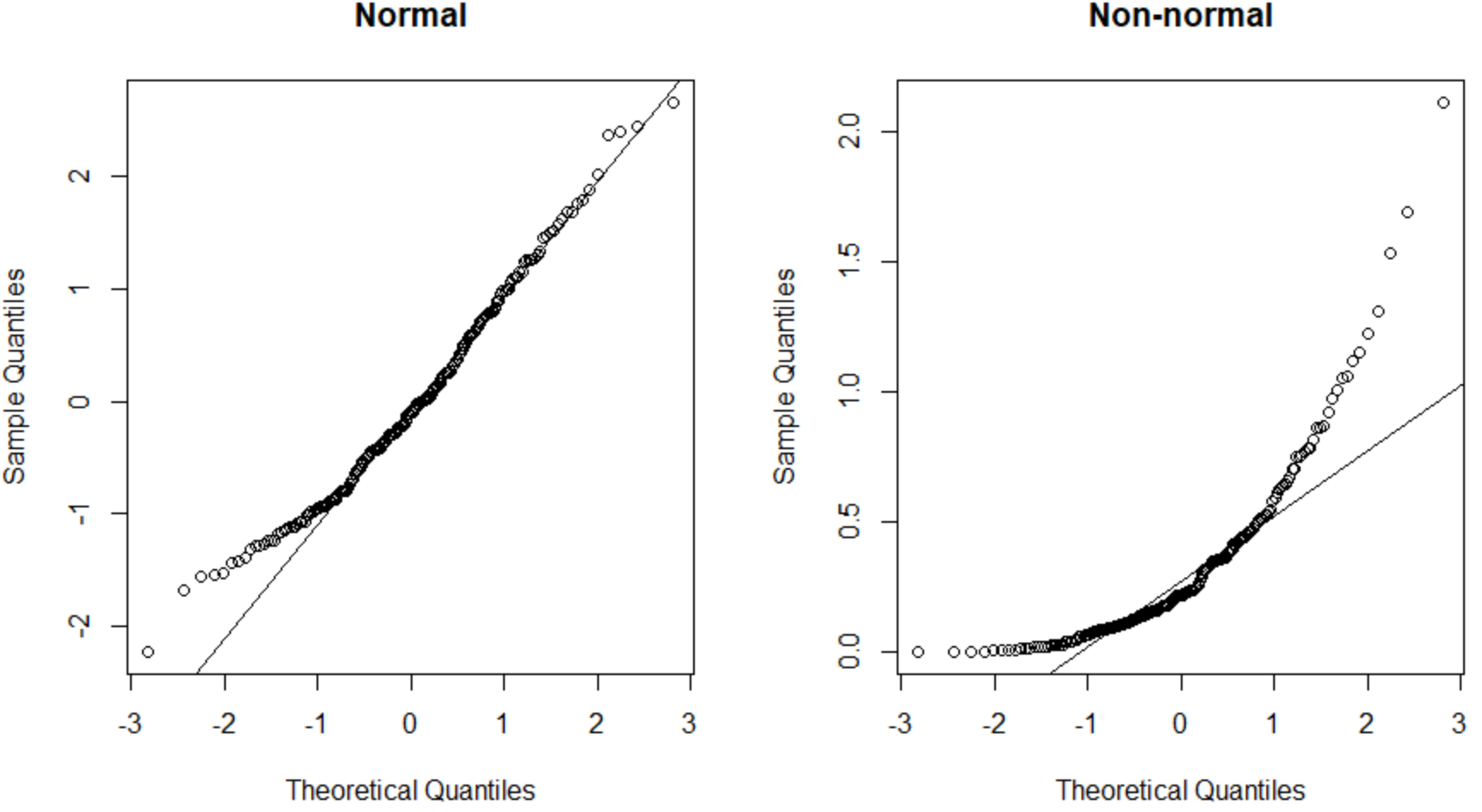
Wykres QQ po lewej stronie przedstawia zbiór danych o rozkładzie normalnym (punkty układają się wzdłuż prostej przekątnej), a wykres QQ po prawej stronie przedstawia zbiór danych o rozkładzie normalnym.

Metoda 3: Wykonaj test Shapiro-Wilka

Poniższy kod pokazuje, jak wykonać test Shapiro-Wilka na zbiorze danych o rozkładzie normalnym i o rozkładzie normalnym w R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform shapiro-wilk test
shapiro. test (normal_data)

	Shapiro-Wilk normality test

data: normal_data
W = 0.99248, p-value = 0.3952

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform shapiro-wilk test
shapiro. test (non_normal_data)

	Shapiro-Wilk normality test

data: non_normal_data
W = 0.84153, p-value = 1.698e-13

Wartość p pierwszego testu jest nie mniejsza niż 0,05, co oznacza, że dane mają rozkład normalny.

Wartość p drugiego testu jest mniejsza niż 0,05, co wskazuje, że dane nie mają rozkładu normalnego.

Metoda 4: Wykonaj test Kołmogorowa-Smirnowa

Poniższy kod pokazuje, jak wykonać test Kołmogorowa-Smirnowa na zbiorze danych o rozkładzie normalnym i o rozkładzie normalnym w R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')

	One-sample Kolmogorov–Smirnov test

data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ') 
	One-sample Kolmogorov–Smirnov test

data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided

Wartość p pierwszego testu jest nie mniejsza niż 0,05, co oznacza, że dane mają rozkład normalny.

Wartość p drugiego testu jest mniejsza niż 0,05, co wskazuje, że dane nie mają rozkładu normalnego.

Jak postępować z nietypowymi danymi

Jeśli dany zbiór danych nie ma rozkładu normalnego, często możemy wykonać jedną z następujących transformacji, aby uzyskać bardziej normalny rozkład:

1. Transformacja logu: przekształć wartości x w log(x) .

2. Transformacja pierwiastka kwadratowego: Przekształć wartości x na √x .

3. Transformacja pierwiastka sześciennego: przekształć wartości x na x ^1/3 .

Wykonując te przekształcenia, zbiór danych ogólnie ma rozkład bardziej normalny.

Przeczytaj ten samouczek , aby zobaczyć, jak wykonać te transformacje w R.

Dodatkowe zasoby

Jak tworzyć histogramy w R
Jak utworzyć i zinterpretować wykres QQ w R
Jak wykonać test Shapiro-Wilka w R
Jak wykonać test Kołmogorowa-Smirnowa w R