Jak wykonać test t dla sparowanych próbek na kalkulatorze ti-84

Test t dla par prób służy do porównania średnich z dwóch próbek, gdy każdą obserwację w jednej próbie można powiązać z obserwacją w drugiej próbie.

W tym samouczku wyjaśniono, jak wykonać test t dla par na kalkulatorze TI-84.

Przykład: Test t dla par próbek na kalkulatorze TI-84

Naukowcy chcą wiedzieć, czy nowy sposób uzdatniania paliwa powoduje zmianę średniego zużycia paliwa przez określony samochód. Aby to sprawdzić, przeprowadzają eksperyment, w którym mierzą mpg 11 samochodów z uzdatnieniem paliwa i bez niego.

Ponieważ każdy samochód jest poddawany zabiegowi, możemy przeprowadzić test t dla par, w którym każdy samochód jest powiązany ze sobą, aby określić, czy istnieje różnica w średnim przebiegu na trasie z uzdatnieniem paliwa i bez niego.

Wykonaj poniższe kroki, aby wykonać test t dla par na kalkulatorze TI-84.

Krok 1: Wprowadź dane.

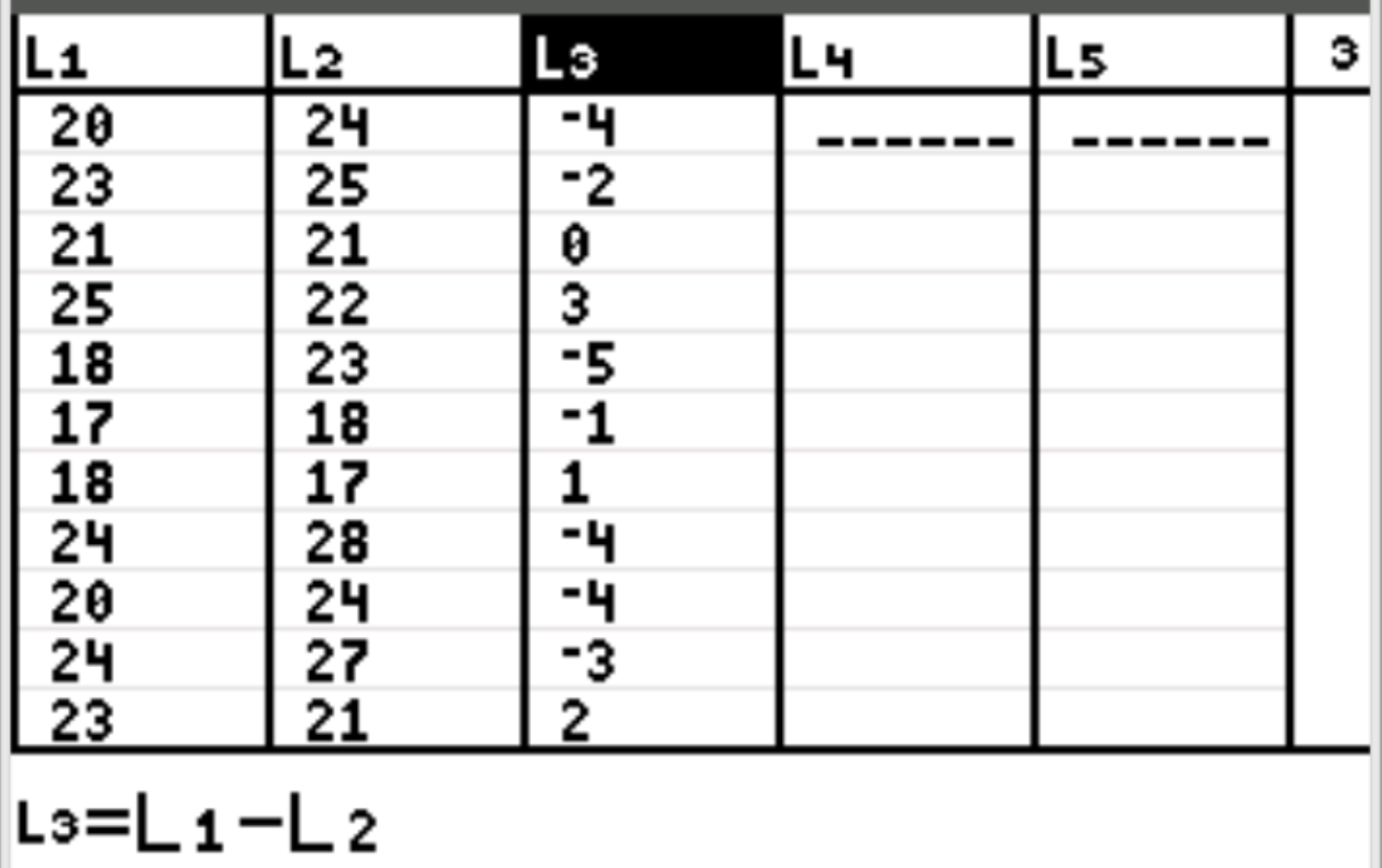
Najpierw wprowadzimy wartości danych dla obu próbek. Naciśnij Stat , następnie naciśnij EDYTUJ . Wpisz następujące wartości dla grupy kontrolnej (bez oczyszczania paliwa) w kolumnie L1 i wartości zmiennej grupy leczenia (otrzymane leczenie paliwem) w kolumnie L2, a następnie różnicę między tymi dwiema wartościami w kolumnie L3.

Uwaga: na górze trzeciej kolumny podświetl L3. Następnie naciśnij 2 i 1 , aby utworzyć L1, po czym naciśnij znak minus, a następnie naciśnij 2 i 2 , aby utworzyć L2. Następnie naciśnij Enter . Każda z wartości w kolumnie L3 zostanie automatycznie wypełniona przy użyciu formuły L1-L2.

Krok 2: Wykonaj test t dla par.

Aby wykonać test t dla par, po prostu przeprowadzimy test t w kolumnie L3, która zawiera wartości różnicy w parach.

Kliknij Statystyka . Przewiń w dół do TESTY . Przewiń do 2:T-Test i naciśnij ENTER .

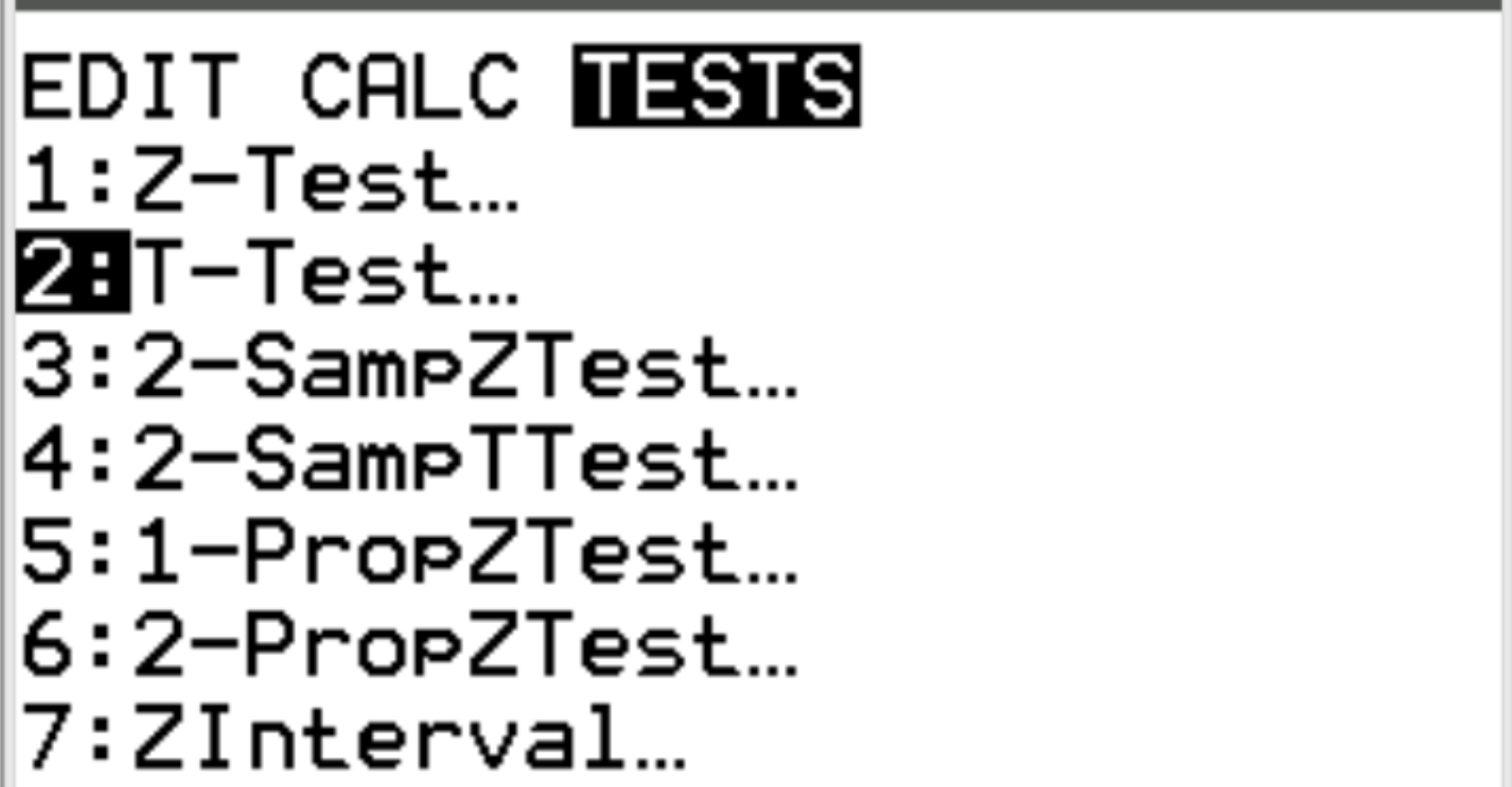
Kalkulator poprosi o podanie następujących informacji:

• Dane wejściowe: Wybierz, czy pracujesz z surowymi danymi (Dane), czy ze statystykami podsumowującymi (Statystyki). W takim przypadku podświetlimy Dane i wciśnij ENTER .
• μ ₀ : Średnia różnica stosowana w hipotezie zerowej. Wpiszemy 0 i wciśnij ENTER .
• Lista: Lista zawierająca różnice między dwiema próbkami. Wpiszemy L3 i wciśniemy ENTER . Uwaga: aby wyświetlić L3, naciśnij 2 , a następnie naciśnij 3 .
• Częstotliwość: Częstotliwość. Zostaw ten zestaw na 1.
• μ : alternatywna hipoteza do zastosowania. Ponieważ przeprowadzamy test dwustronny, podświetlimy ≠ μ ₀ i wciśniemy ENTER . Oznacza to, że naszą hipotezą alternatywną jest μ≠0. Pozostałe dwie opcje zostaną użyte dla testów lewych (<μ ₀ ) i testów prawych (>μ ₀ ).

Na koniec podświetl Oblicz i naciśnij ENTER .

Krok 3: Interpretacja wyników.

Nasz kalkulator automatycznie wygeneruje wyniki testu t dla jednej próby:

Oto jak interpretować wyniki:

• μ≠0 : Jest to alternatywna hipoteza testu.
• t=-1,8751 : To jest statystyka testu t.
• p=0,0903 : Jest to wartość p odpowiadająca statystyce testowej.
• x =-1,5455 . Jest to średnia różnica w porównaniu z grupą 1 – grupą 2.
• _sx =2,7336 . Jest to odchylenie standardowe różnic.
• n=11 : Jest to całkowita liczba sparowanych próbek.

Ponieważ wartość p testu (0,0903) jest nie mniejsza niż 0,05, nie udaje nam się odrzucić hipotezy zerowej.

Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że istnieje różnica między średnim poziomem mpg w obu grupach. Mówiąc najprościej, nie mamy wystarczających dowodów, aby stwierdzić, że obróbka paliwa wpływa na mpg.