Jak wykonać test breuscha-pagana w programie excel
Test Breuscha-Pagana służy do określenia, czy w analizie regresji występuje heteroskedastyczność .
W tym samouczku wyjaśniono, jak wykonać test Breuscha-Pagana w programie Excel.
Przykład: test Breuscha-Pagana w Excelu
W tym przykładzie użyjemy następującego zbioru danych opisującego atrybuty 10 koszykarzy.
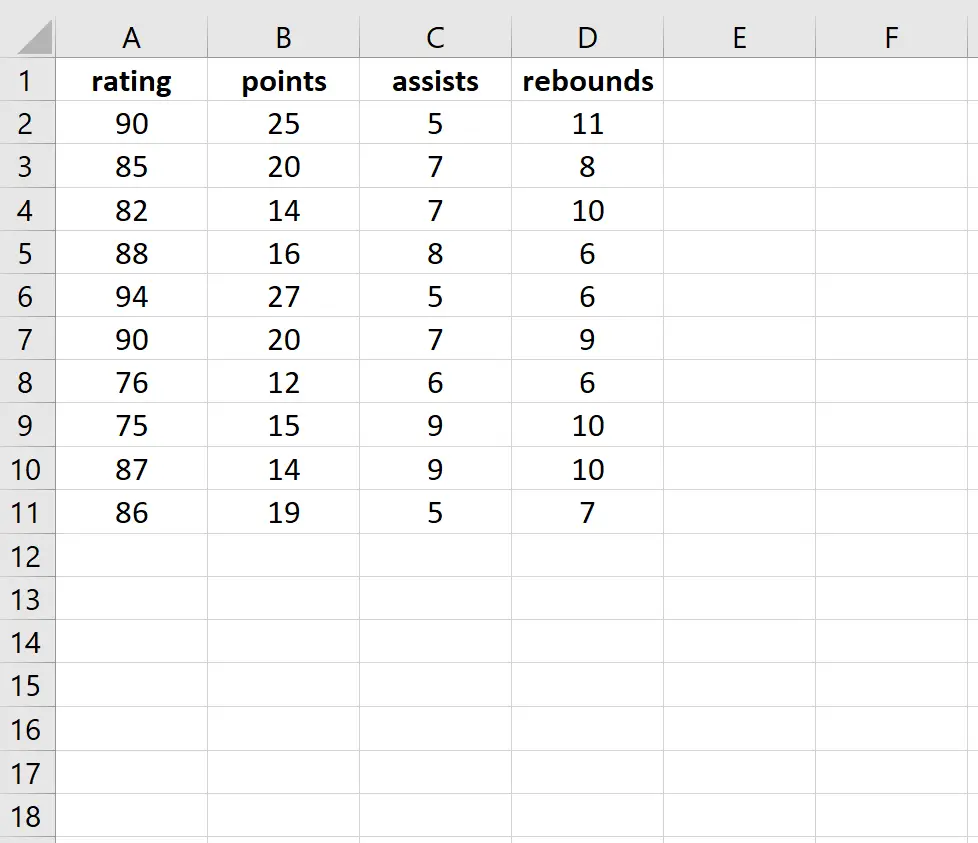
Dopasujemy model regresji liniowej, wykorzystując punktację jako zmienną odpowiedzi oraz punkty, asysty i zbiórki jako zmienne objaśniające. Następnie przeprowadzimy test Breuscha-Pagana, aby określić, czy w regresji występuje heteroskedastyczność.
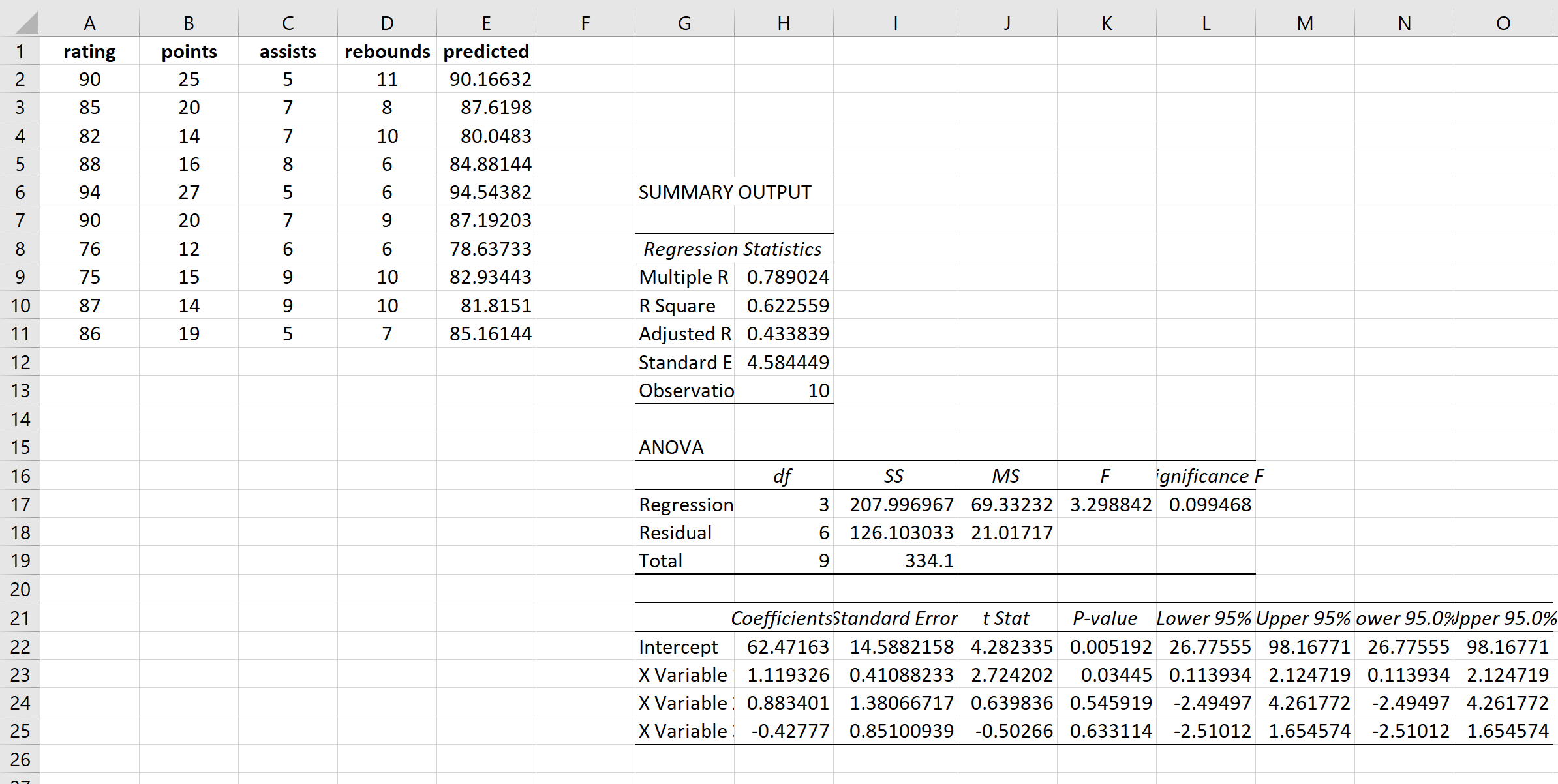
Krok 1: Wykonaj wielokrotną regresję liniową.
Na górnej wstążce programu Excel przejdź do karty Dane i kliknij Analiza danych. Jeśli nie widzisz tej opcji, musisz najpierw zainstalować bezpłatne oprogramowanie Analysis ToolPak .

Po kliknięciu Analiza danych pojawi się nowe okno. Wybierz opcję Regresja i kliknij OK. Wypełnij niezbędne tabele dla zmiennych odpowiedzi i zmiennych objaśniających, a następnie kliknij OK.
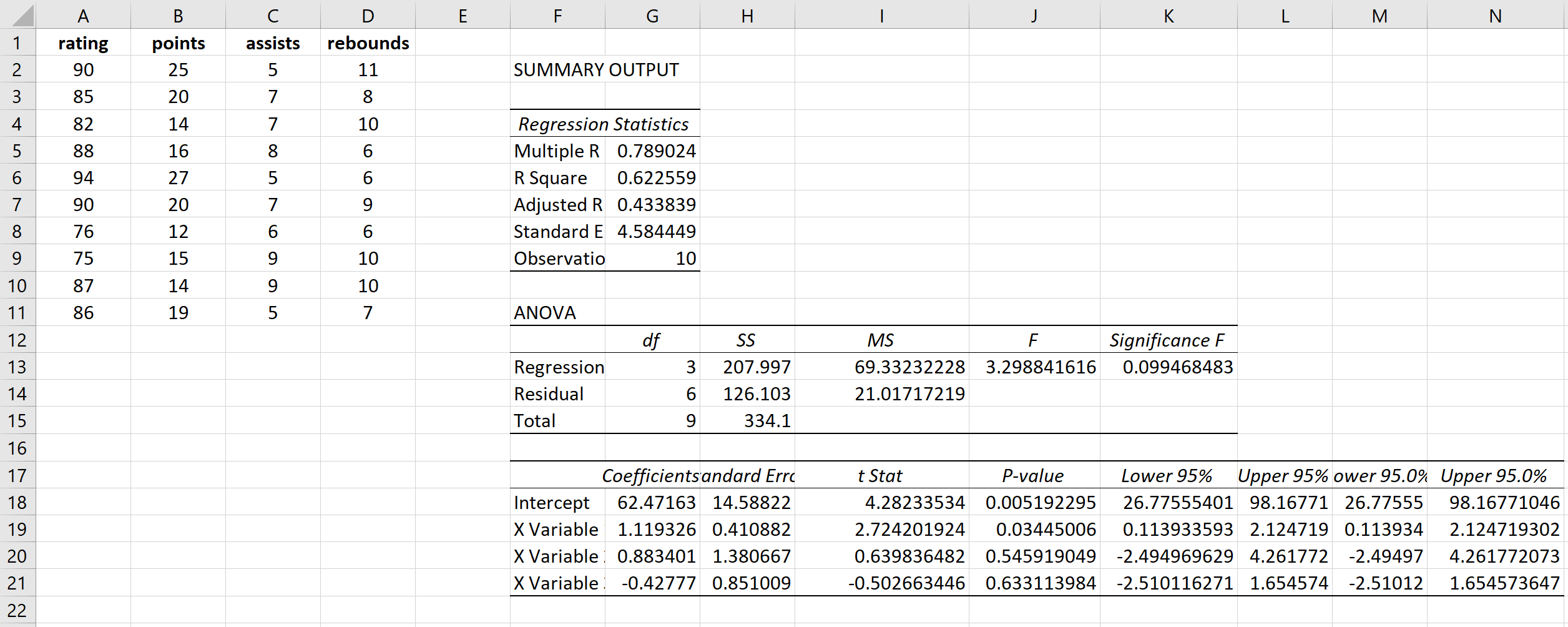
Daje to następujący wynik:
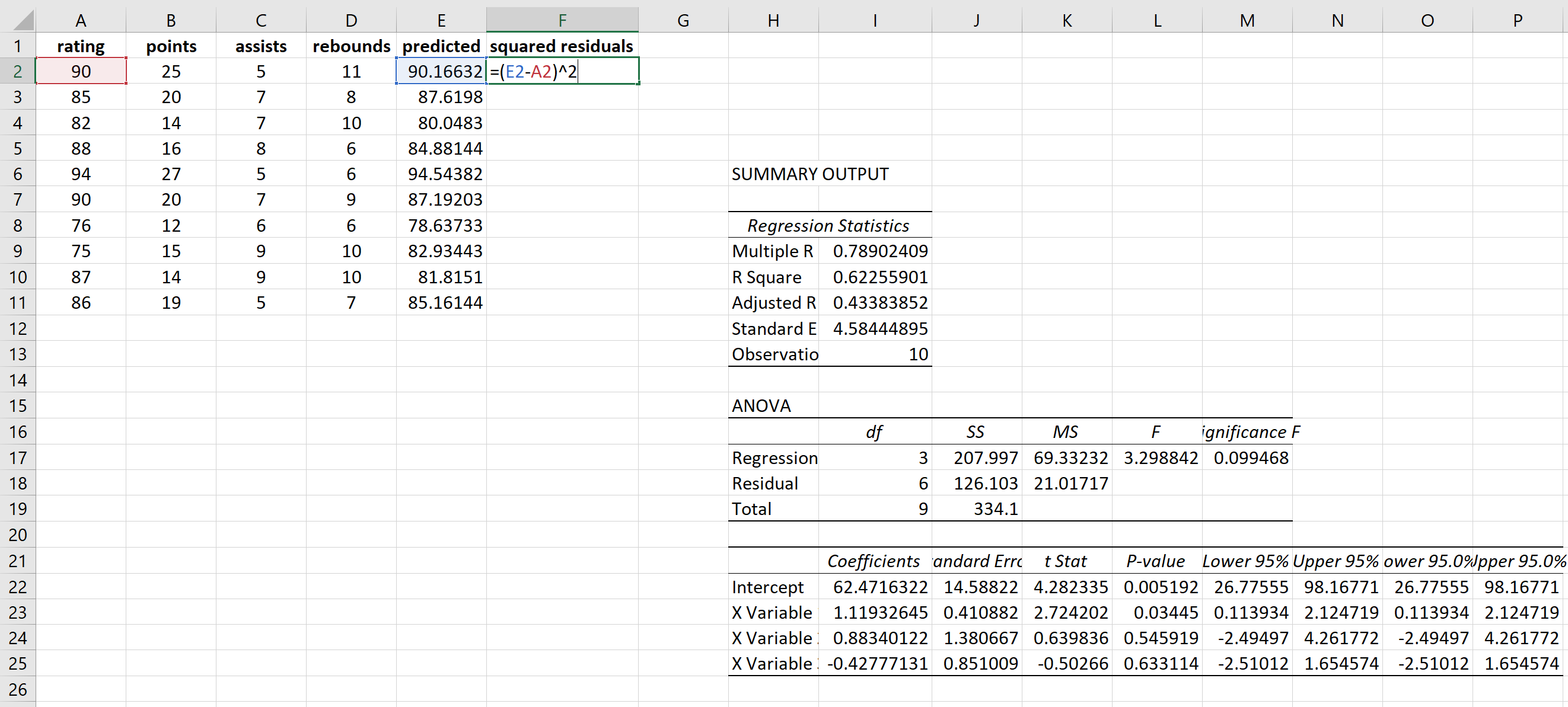
Krok 2: Oblicz kwadraty reszt.
Następnie obliczymy przewidywane wartości i kwadraty reszt dla każdej wartości odpowiedzi. Do obliczenia przewidywanych wartości wykorzystamy współczynniki z wyniku regresji:
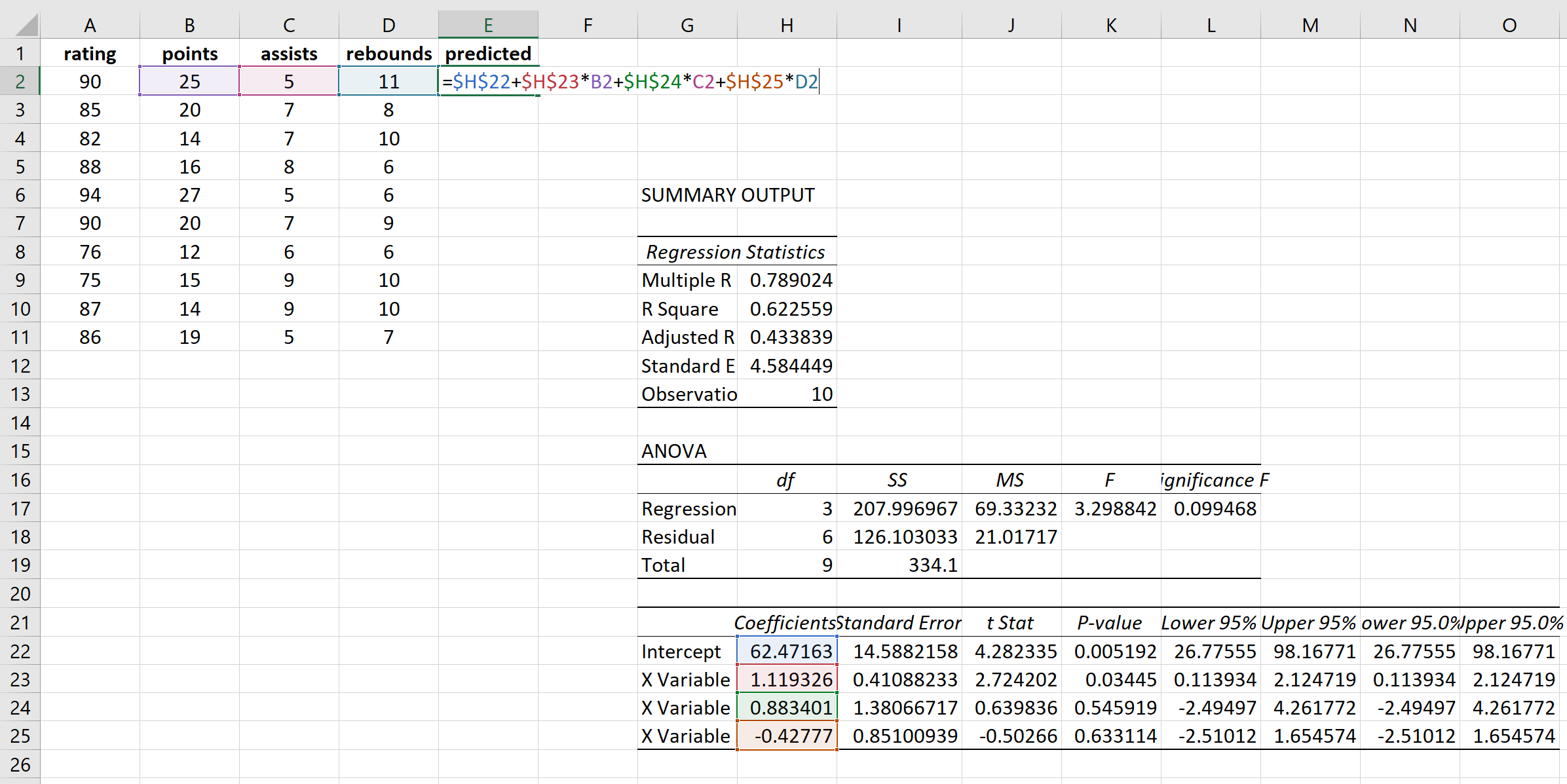
Do uzyskania każdej przewidywanej wartości użyjemy tego samego wzoru:
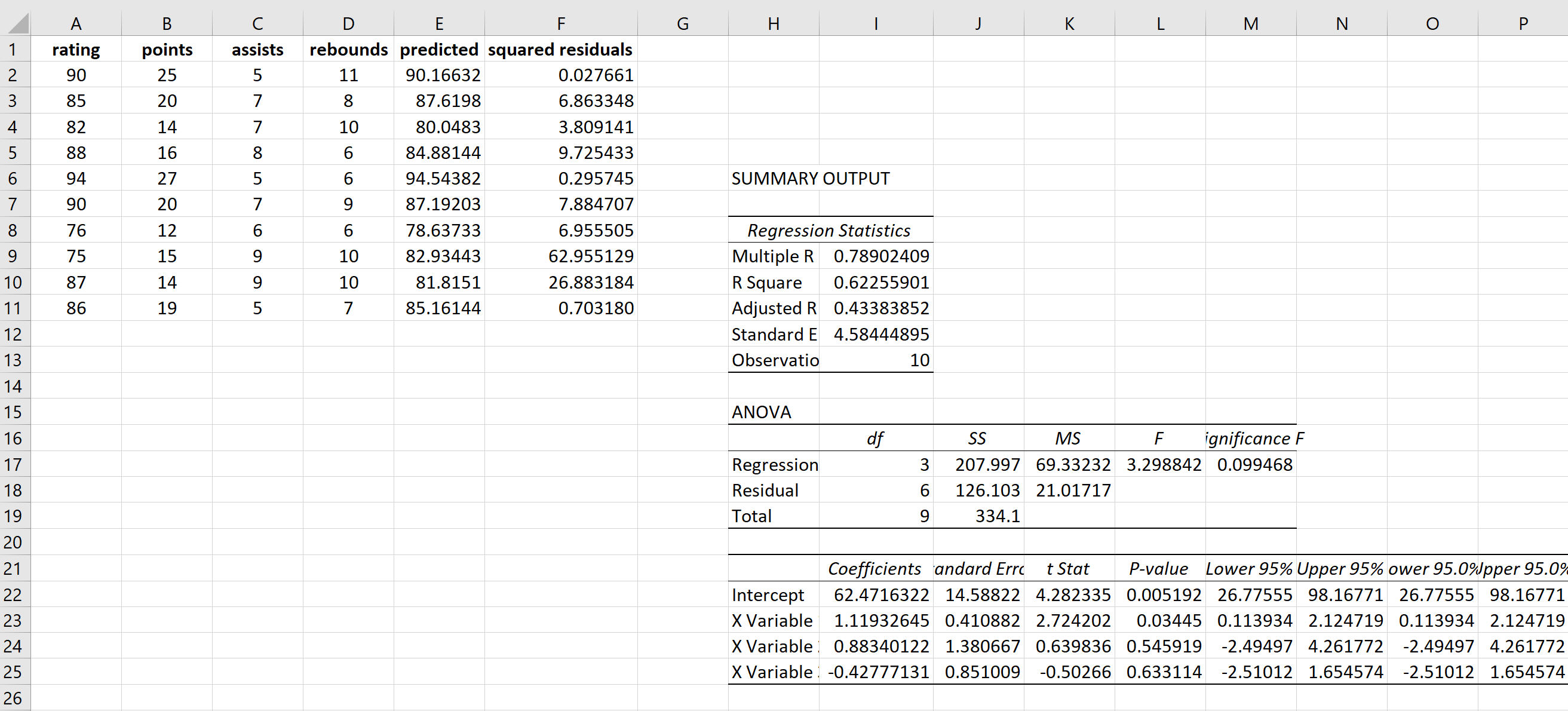
Następnie obliczymy kwadraty reszt dla każdej prognozy:
Użyjemy tego samego wzoru, aby uzyskać każdy pozostały kwadrat:
Krok 3: Wykonaj nową wielokrotną regresję liniową, używając kwadratów reszt jako wartości odpowiedzi.
Następnie wykonamy te same kroki co poprzednio, aby przeprowadzić wielokrotną regresję liniową, używając punktów, asyst i zbiórek jako zmiennych objaśniających, z tą różnicą, że tym razem jako wartości odpowiedzi użyjemy kwadratów reszt. Oto wynik tej regresji:
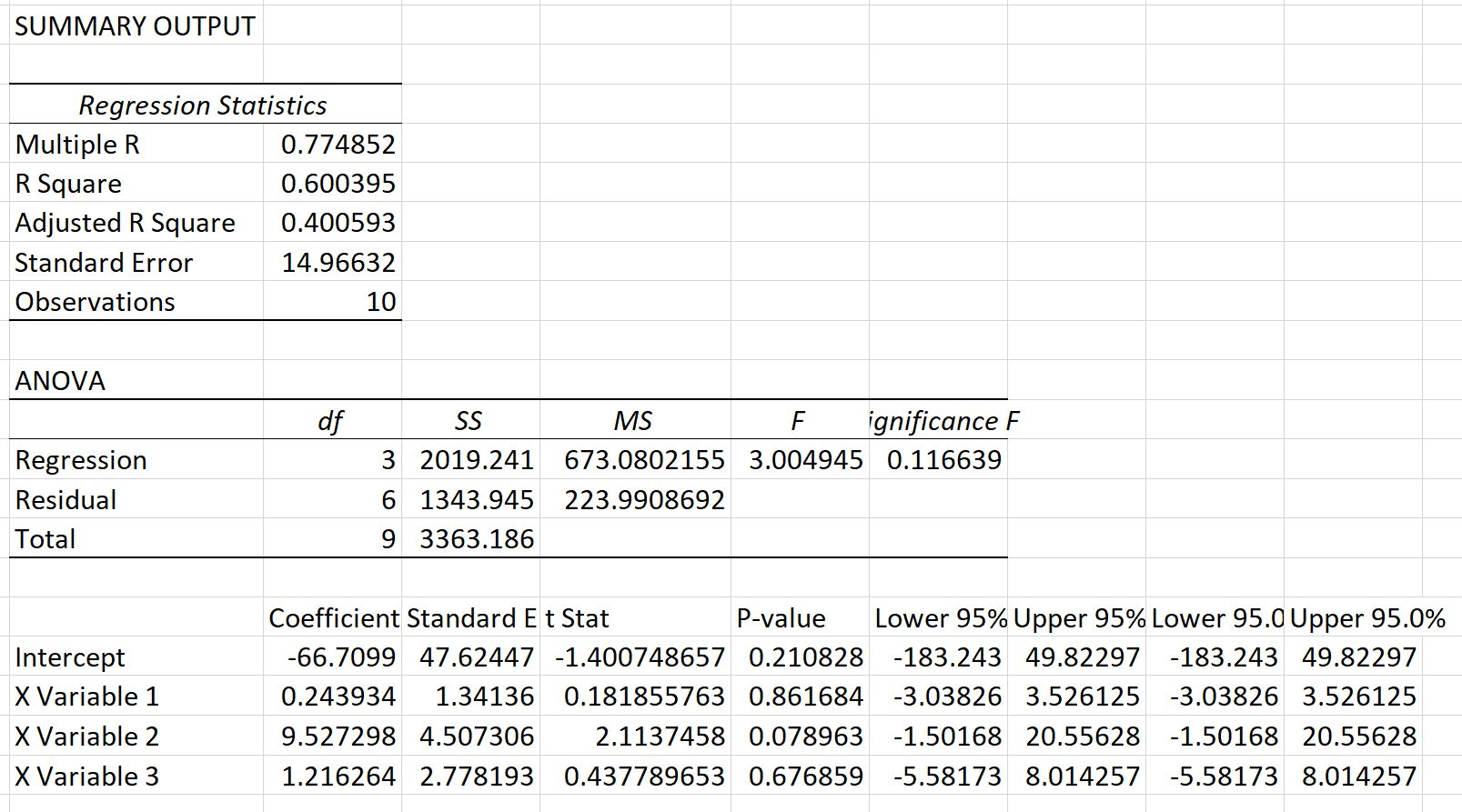
Krok 4: Wykonaj test Breuscha-Pagana.
Na koniec przeprowadzimy test Breuscha-Pagana, aby sprawdzić, czy w pierwotnej regresji występowała heteroskedastyczność.
Najpierw obliczymy statystykę testu Chi-kwadrat, korzystając ze wzoru:
X 2 = n*R 2 nowy
Złoto:
n = liczba obserwacji
R 2 nowy = R Kwadrat „nowej” regresji, w której jako zmienną odpowiedzi wykorzystano kwadraty reszt.
W naszym przykładzie X 2 = 10 * 0,600395 = 6,00395 .
Następnie znajdziemy wartość p powiązaną z tą statystyką testową. Możemy w tym celu skorzystać z następującej formuły w programie Excel:
= ROZKŁ.CHISQ.RT(statystyka testowa, stopnie swobody)
W naszym przypadku stopnie swobody są liczbą określoną dla regresji df na wyjściu. W tym przypadku jest to 3. Zatem nasza formuła wygląda następująco:
= ROZKŁ.CHISQ.RT(6,00395; 3) = 0,111418 .
Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej. Nie mamy wystarczających dowodów, aby twierdzić, że heteroskedastyczność jest obecna w pierwotnym modelu regresji.