Jak wykonać test log rank w r

Test log-rank jest najczęstszym sposobem porównywania krzywych przeżycia między dwiema grupami.

W tym teście przyjęto następujące założenia :

H ₀ : Nie ma różnicy w przeżyciu pomiędzy obiema grupami.

H _A : Istnieje różnica w przeżywalności pomiędzy obiema grupami.

Jeśli wartość p testu jest poniżej pewnego poziomu istotności (np. α = 0,05), wówczas możemy odrzucić hipotezę zerową i stwierdzić, że istnieją wystarczające dowody, aby stwierdzić, że istnieje różnica w przeżywalności pomiędzy obiema grupami.

Aby wykonać test log-rank w R, możemy użyć funkcji survdiff() z pakietu survival , która wykorzystuje następującą składnię:

survdiff(Surv(czas, status) ~ predyktory, dane)

Ta funkcja zwraca statystykę testu chi-kwadrat i odpowiadającą jej wartość p.

Poniższy przykład pokazuje, jak używać tej funkcji do wykonywania testu log-rank w języku R.

Przykład: Test Log Rank w R

W tym przykładzie użyjemy zestawu danych dotyczących jajników z pakietu przeżycia . Ten zbiór danych zawiera następujące informacje na temat 26 pacjentów:

• Czas przeżycia (w miesiącach) po zdiagnozowaniu raka jajnika
• Niezależnie od tego, czy czas przetrwania był cenzurowany
• Rodzaj otrzymanego leczenia (rx = 1 lub rx = 2)

Poniższy kod pokazuje, jak wyświetlić pierwsze sześć wierszy tego zbioru danych:

 library (survival)

#view first six rows of dataset
head(ovarian)

  futime fustat age resid.ds rx ecog.ps
1 59 1 72.3315 2 1 1
2 115 1 74.4932 2 1 1
3 156 1 66.4658 2 1 2
4 421 0 53.3644 2 2 1
5,431 1 50.3397 2 1 1
6 448 0 56.4301 1 1 2

Poniższy kod pokazuje, jak przeprowadzić test log-rank w celu ustalenia, czy istnieje różnica w przeżyciu między pacjentami, którzy otrzymali różne metody leczenia:

 #perform log rank test
survdiff(Surv(futime, fustat) ~ rx, data=ovarian)

Call:
survdiff(formula = Surv(futime, fustat) ~ rx, data = ovarian)

      N Observed Expected (OE)^2/E (OE)^2/V
rx=1 13 7 5.23 0.596 1.06
rx=2 13 5 6.77 0.461 1.06

 Chisq= 1.1 on 1 degrees of freedom, p= 0.3 

Statystyka testu Chi-kwadrat wynosi 1,1 z 1 stopniem swobody, a odpowiadająca jej wartość p wynosi 0,3 . Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej.

Innymi słowy, nie mamy wystarczających dowodów, aby stwierdzić, że istnieje statystycznie istotna różnica w przeżyciu pomiędzy tymi dwoma sposobami leczenia.

Możemy również wykreślić krzywe przeżycia dla każdej grupy, używając następującej składni:

 #plot survival curves for each treatment group
plot(survfit(Surv(futime, fustat) ~ rx, data = ovarian), 
     xlab = " Time ", 
     ylab = “ Overall survival probability ”)

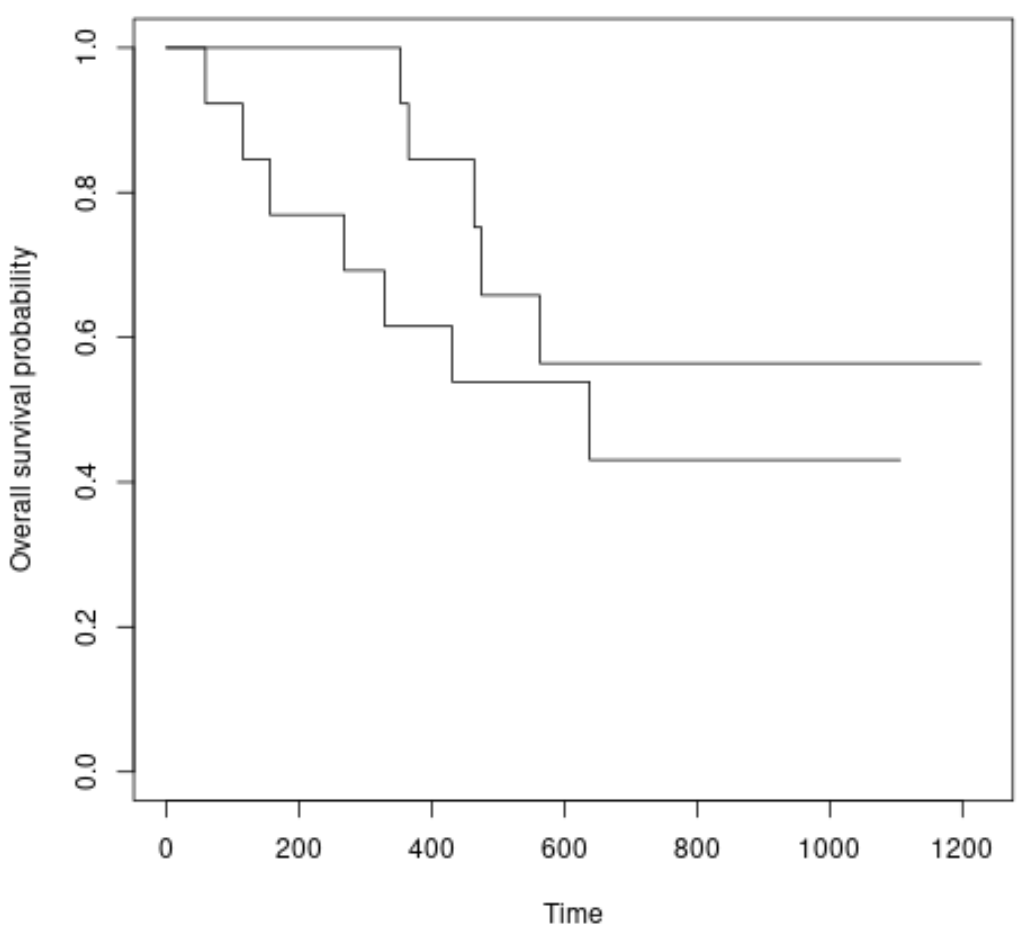
Widzimy, że krzywe przeżycia są nieco inne, ale test log-rank powiedział nam, że różnica nie jest istotna statystycznie.