Jak wykonać test rangi podpisanej wilcoxona

Test rang ze znakiem Wilcoxona jest nieparametryczną wersją testu t dla par . Służy do sprawdzenia, czy istnieje znacząca różnica między dwiema średnimi z populacji.

Kiedy stosować test rang ze znakiem Wilcoxona

Jeśli chcesz zastosować test t dla par, ale rozkład różnic między parami ma rozkład znacznie odbiegający od normalnego, użyj testu rangi podpisanej Wilcoxona.

Najłatwiejszym sposobem ustalenia, czy różnice nie mają rozkładu normalnego, jest utworzenie histogramu różnic i sprawdzenie, czy mają one rozkład w miarę normalny, w kształcie dzwonu.

Należy pamiętać, że test t dla par jest dość odporny na odchylenia od normalności, więc odchylenie od rozkładu normalnego musi być na tyle duże, aby uzasadniać zastosowanie testu rangi podpisanej Wilcoxona.

Jak przystąpić do testu rangi podpisanej Wilcoxona

Poniższy przykład ilustruje sposób przeprowadzenia testu rangi podpisanej Wilcoxona.

Trener koszykówki chce wiedzieć, czy określony program treningowy zwiększa liczbę rzutów wolnych wykonywanych przez jego zawodników. Aby to sprawdzić, poprosił 15 zawodników, aby każdy wykonał po 20 rzutów wolnych przed i po programie treningowym.

Ponieważ każdego zawodnika można „sparować” ze sobą, trener zaplanował zastosowanie testu t dla par, aby określić, czy istnieje znacząca różnica pomiędzy średnią liczbą rzutów wolnych wykonanych przed i po programie treningowym. szkolenie.

Rozkład różnic okazuje się jednak nienormalny, dlatego coach stosuje zamiast tego test rang ze znakiem Wilcoxona.

Poniższa tabela przedstawia liczbę rzutów wolnych wykonanych (z 20 prób) przez każdego z 15 zawodników przed i po programie treningowym:

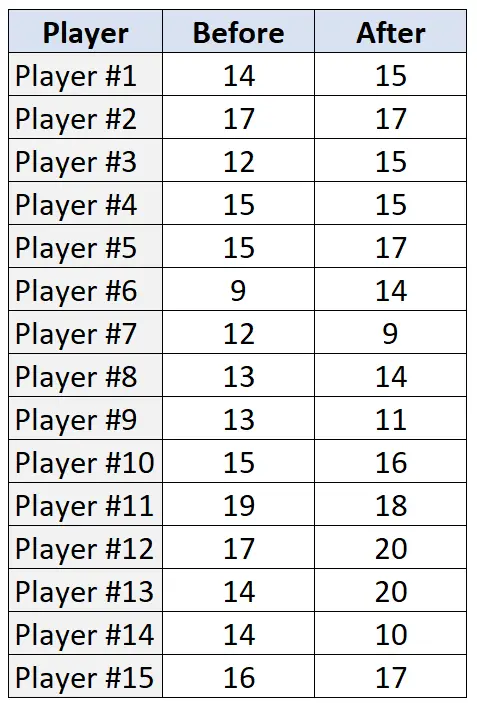
Krok 1: Podaj hipotezę zerową i alternatywną.

H ₀ : Mediana różnicy pomiędzy dwiema grupami wynosi zero.

H _A : Mediana różnicy jest ujemna. (np. gracze wykonują mniej rzutów wolnych przed wzięciem udziału w programie treningowym)

Krok 2: Znajdź różnicę i różnicę bezwzględną dla każdej pary.

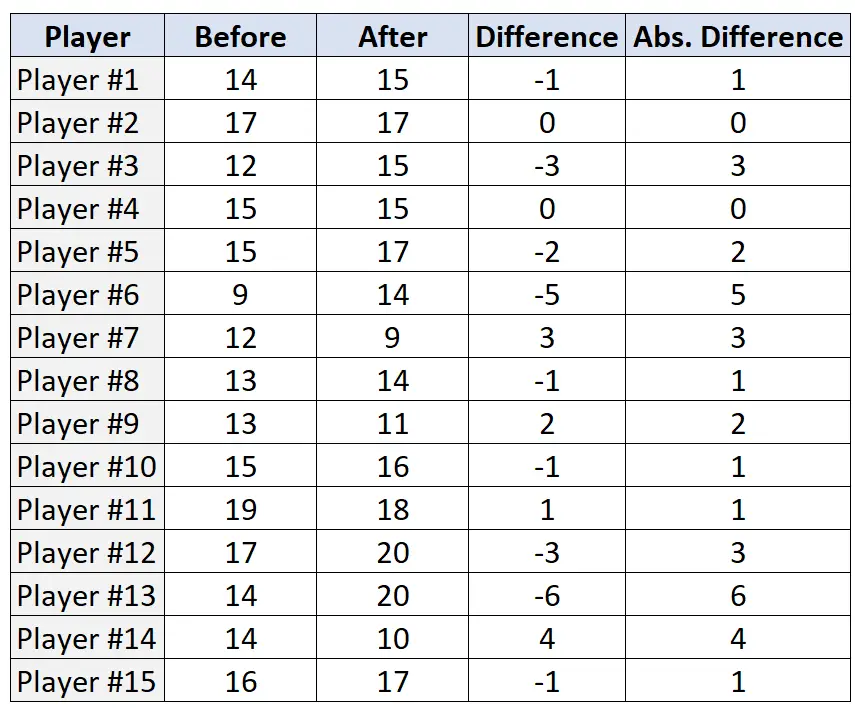
Krok 3: Uszereguj pary na podstawie różnic bezwzględnych i przypisz rangę od najmniejszej do największej różnicy bezwzględnej. Ignoruj pary, których różnica bezwzględna wynosi „0” i przydzielaj średnie rangi w przypadku remisu.

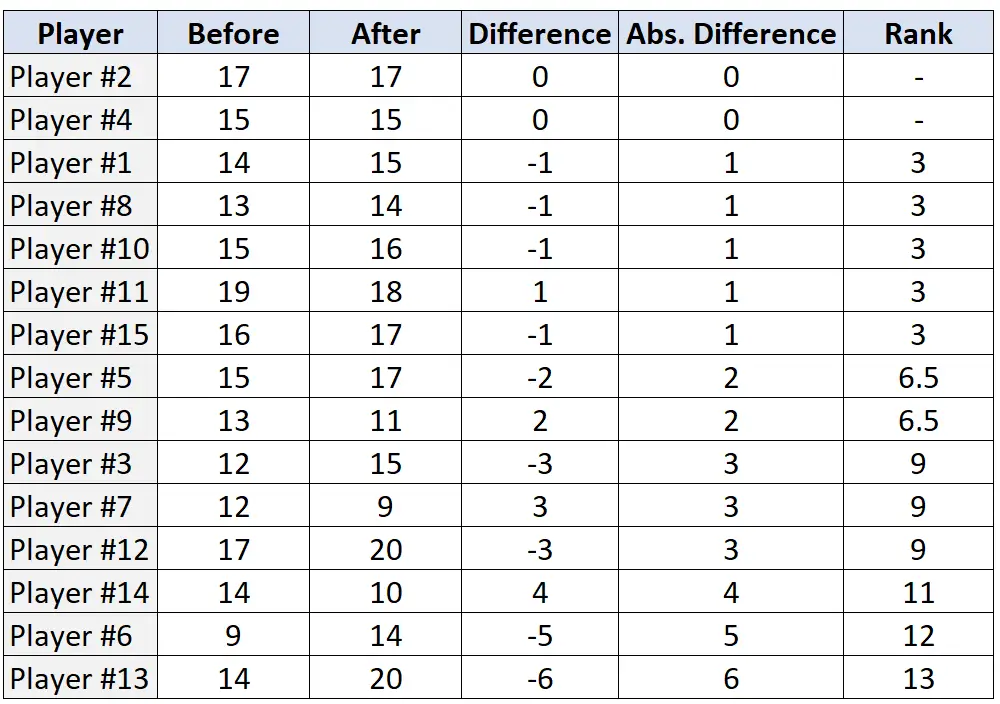
Krok 4: Znajdź sumę rang dodatnich i ujemnych.

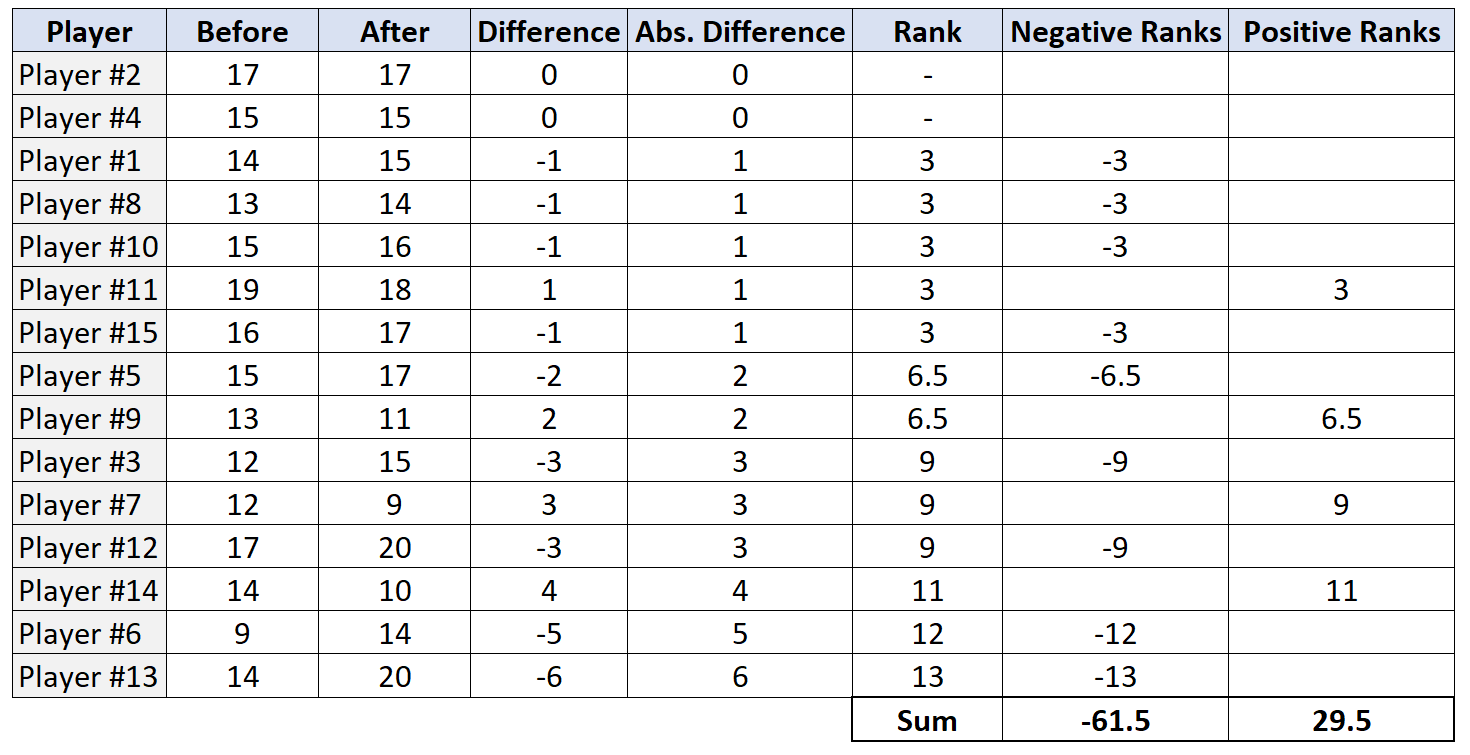
Krok 5: Odrzuć lub nie odrzucaj hipotezy zerowej.

Statystyka testowa W jest najmniejszą z wartości bezwzględnych rang dodatnich i rang ujemnych. W tym przypadku najmniejsza wartość to 29,5. Zatem nasza statystyka testowa wynosi W = 29,5 .

Aby określić, czy powinniśmy odrzucić hipotezę zerową, czy nie, możemy odwołać się do wartości krytycznej znalezionej w tabeli wartości krytycznych testu rang ze znakami Wilcoxona, która odpowiada n i wybranemu poziomowi alfa.

Jeśli nasza statystyka testowa W jest mniejsza lub równa wartości krytycznej z tabeli, możemy odrzucić hipotezę zerową. W przeciwnym razie nie odrzucimy hipotezy zerowej.

Wartość krytyczna odpowiadająca poziomowi alfa wynoszącemu 0,05 i n = 13 (całkowita liczba par minus dwie, dla których nie obliczyliśmy rangi, ponieważ zaobserwowano różnicę wynoszącą 0) wynosi 17 .

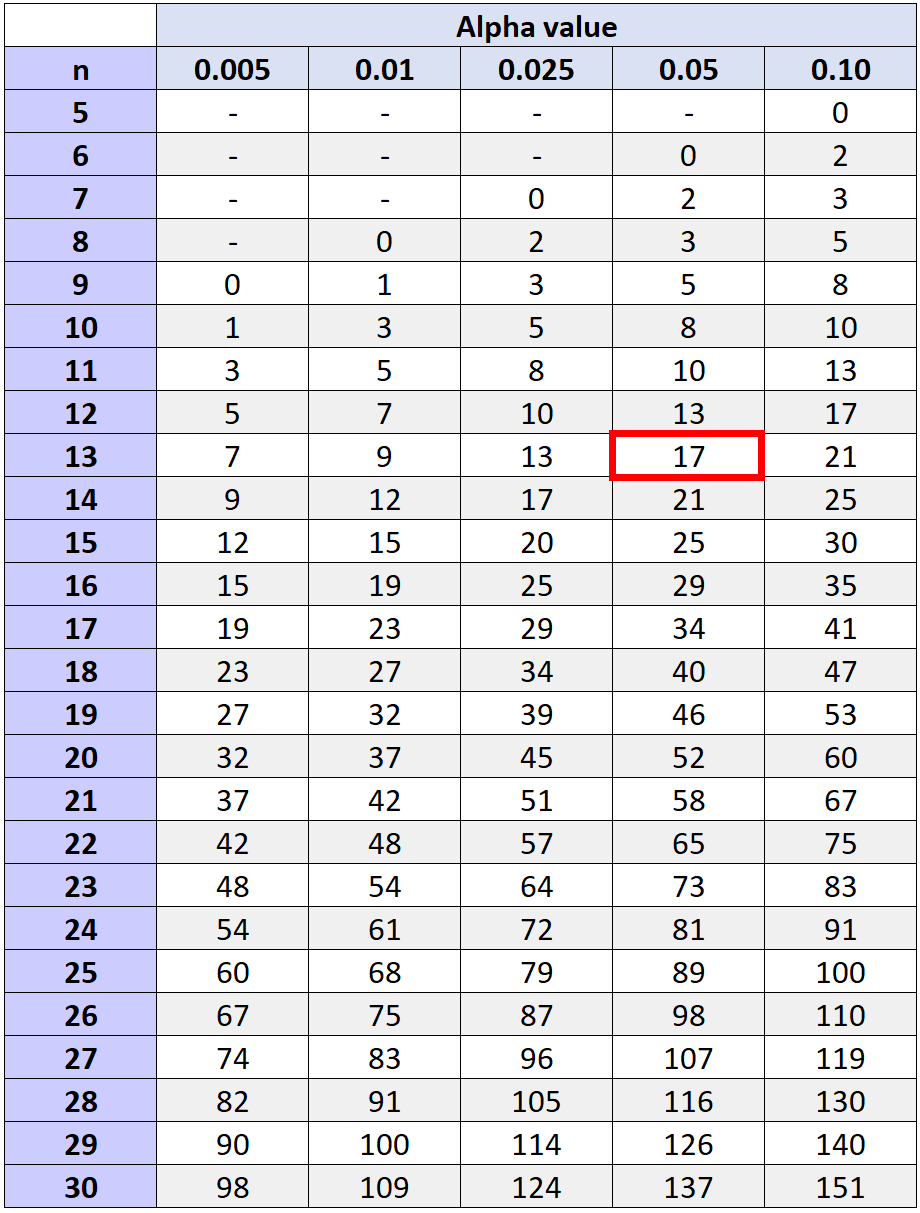
Ponieważ nasza statystyka testowa (W = 29,5) jest nie mniejsza lub równa 17, nie udaje nam się odrzucić hipotezy zerowej. Nie mamy wystarczających dowodów, aby stwierdzić, że program treningowy skutkuje znaczącym wzrostem liczby rzutów wolnych wykonywanych przez zawodników.

Uwaga: Jeśli chcesz przeprowadzić test przy użyciu kalkulatora, a nie ręcznie, użyj kalkulatora testu rang podpisanych Wilcoxona .