Jak wykonać test rang ze znakiem wilcoxona w r

Test rangi znaku Wilcoxona jest nieparametryczną wersją testu t dla par . Służy do sprawdzenia, czy istnieje znacząca różnica między średnimi z dwóch populacji, gdy rozkładu różnic między dwiema próbami nie można uznać za normalny.

W tym samouczku wyjaśniono, jak wykonać test rang ze znakiem Wilcoxona w języku R.

Przykład: Test rangowy podpisany Wilcoxonem w R

Załóżmy, że trener koszykówki chce wiedzieć, czy określony program treningowy zwiększa liczbę rzutów wolnych wykonywanych przez jego zawodników. Aby to sprawdzić, poprosił 15 zawodników, aby każdy wykonał po 20 rzutów wolnych przed i po programie treningowym.

Ponieważ każdego zawodnika można „sparować” ze sobą, trener zaplanował zastosowanie testu t dla par, aby określić, czy istnieje znacząca różnica pomiędzy średnią liczbą rzutów wolnych wykonanych przed i po programie treningowym. szkolenie. Jednakże rozkład różnic okazuje się nienormalny, dlatego trener zamiast tego wykorzystuje test Wilcoxona Signed-Rank.

Poniższa tabela przedstawia liczbę rzutów wolnych wykonanych (z 20 prób) przez każdego z 15 zawodników przed i po programie treningowym:

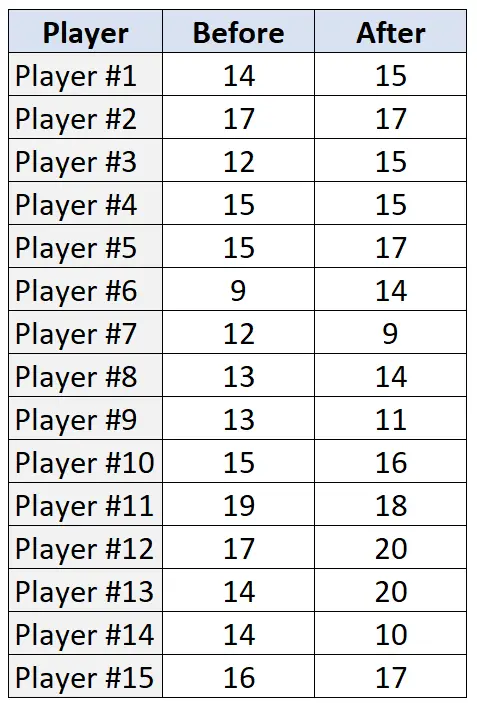
Aby wykonać test rang ze znakiem Wilcoxona na tych danych w R, możemy użyć funkcji wilcox.test() , która wykorzystuje następującą składnię:

wilcox.test(x, y, parzysty = PRAWDA)

Złoto:

• x, y: dwa wektory wartości danych
• sparowane: ustawienie na TRUE mówi R, że nasze dwa wektory zawierają sparowane dane

Poniższy kod ilustruje sposób użycia tej funkcji do przeprowadzenia testu Wilcoxon Signed-Rank na tych danych:

 #create the two vectors of data
before <- c(14, 17, 12, 15, 15, 9, 12, 13, 13, 15, 19, 17, 14, 14, 16)
after <- c(15, 17, 15, 15, 17, 14, 9, 14, 11, 16, 18, 20, 20, 10, 17)

#perform Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE)

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.275
alternative hypothesis: true location shift is not equal to 0

Statystyka testowa wynosi 29,5 , a odpowiadająca jej wartość p wynosi 0,275 . Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej. Nie stwierdzono istotnej statystycznie różnicy w liczbie rzutów wolnych przed i po wzięciu udziału w programie treningowym.

Domyślnie ta funkcja wykonuje dwustronny test Wilcoxona ze znakiem rangi, ale możesz określić test leworęczny lub praworęczny, używając alternatywnego argumentu:

 #perform left-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="less")

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.1375
alternative hypothesis: true location shift is less than 0

#perform right-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="greater")

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.8774
alternative hypothesis: true location shift is greater than 0

Dodatkowe zasoby

Wprowadzenie do testu rang podpisanych Wilcoxona
Kalkulator testu miejsca podpisanego Wilcoxona