Jak wykonać test scheffe w sas-ie

Jednoczynnikową ANOVA stosuje się do określenia, czy istnieje statystycznie istotna różnica pomiędzy średnimi z trzech lub więcej niezależnych grup.

Jeśli ogólna wartość p tabeli ANOVA jest poniżej pewnego poziomu istotności, wówczas mamy wystarczające dowody, aby stwierdzić, że co najmniej jedna ze średnich grupowych różni się od pozostałych.

Nie mówi nam to jednak , które grupy różnią się od siebie. To po prostu mówi nam, że nie wszystkie średnie grupowe są równe.

Aby dokładnie wiedzieć, które grupy się od siebie różnią, należy przeprowadzićtest post hoc .

Jednym z najczęściej stosowanych testów post hoc jest test Scheffe’a , który pozwala na dokonywanie porównań parami pomiędzy średnimi każdej grupy, kontrolując jednocześnie współczynnik błędu rodzinnego .

Poniższy przykład pokazuje, jak wykonać test Scheffe w R.

Przykład: test Scheffe’a w SAS-ie

Załóżmy, że badacz rekrutuje 30 studentów do udziału w badaniu. Studenci są losowo przydzielani do stosowania jednej z trzech metod nauki w celu przygotowania się do egzaminu.

Do utworzenia tego zbioru danych w SAS-ie możemy użyć następującego kodu:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 76
At 77
At 77
At 81
At 82
At 82
At 83
At 84
At 85
At 89
B 81
B 82
B 83
B 83
B 83
B 84
B 87
B90
B92
B93
C 77
C 78
C 79
C 88
C 89
C 90
C 91
C 95
C 98
C 98
;
run ;

Następnie użyjemy proc ANOVA do wykonania jednokierunkowej ANOVA:

 /*perform one-way ANOVA with Scheffe's post-hoc test*/
proc ANOVA data = my_data;
classMethod ;
modelScore = Method;
means Method / scheffe cldiff ;
run;

Uwaga : Zastosowaliśmy zestawienie średnich wraz z opcjami Scheffe’a i Cldiffa , aby określić, że należy przeprowadzić test post-hoc Scheffe’a (z przedziałami ufności), jeśli ogólna wartość p z jednoczynnikowej analizy ANOVA jest statystycznie istotna.

Najpierw przeanalizujemy tabelę ANOVA w wyniku:

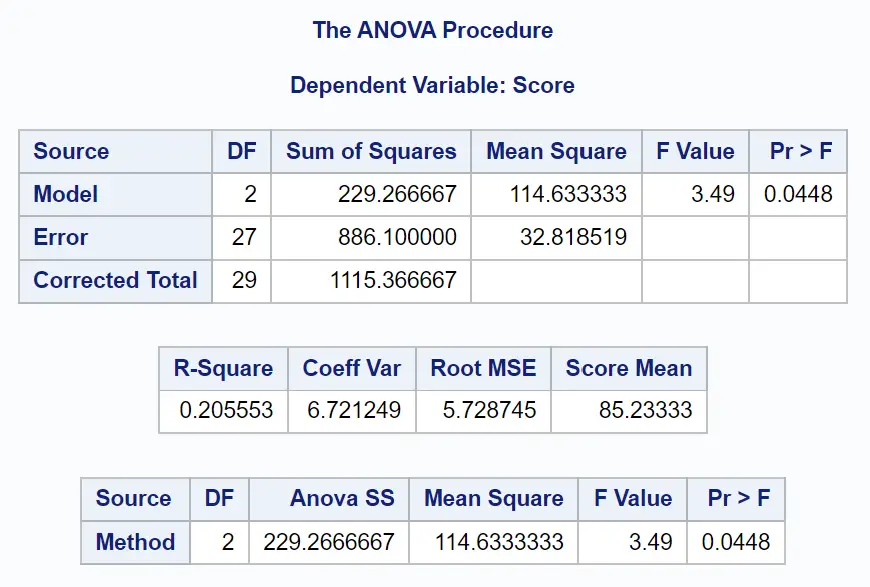
Z tej tabeli możemy zobaczyć:

• Ogólna wartość F: 3,49
• Odpowiednia wartość p: 0,0448

Przypomnijmy, że jednokierunkowa analiza ANOVA wykorzystuje następujące hipotezy zerowe i alternatywne:

• H ₀ : Wszystkie średnie grupowe są równe.
• H _A : Co najmniej jedna średnia grupowa jest inna   odpoczynek.

Ponieważ wartość p tabeli ANOVA (0,0448) jest mniejsza niż α = 0,05, odrzucamy hipotezę zerową.

To mówi nam, że średni wynik egzaminu nie jest równy w przypadku trzech metod badania.

Powiązane: Jak interpretować wartość F i wartość P w ANOVA

Aby dokładnie określić, które średnie grupowe są różne, należy odwołać się do tabeli wyników końcowych, która przedstawia wyniki testów post-hoc Scheffe’a:

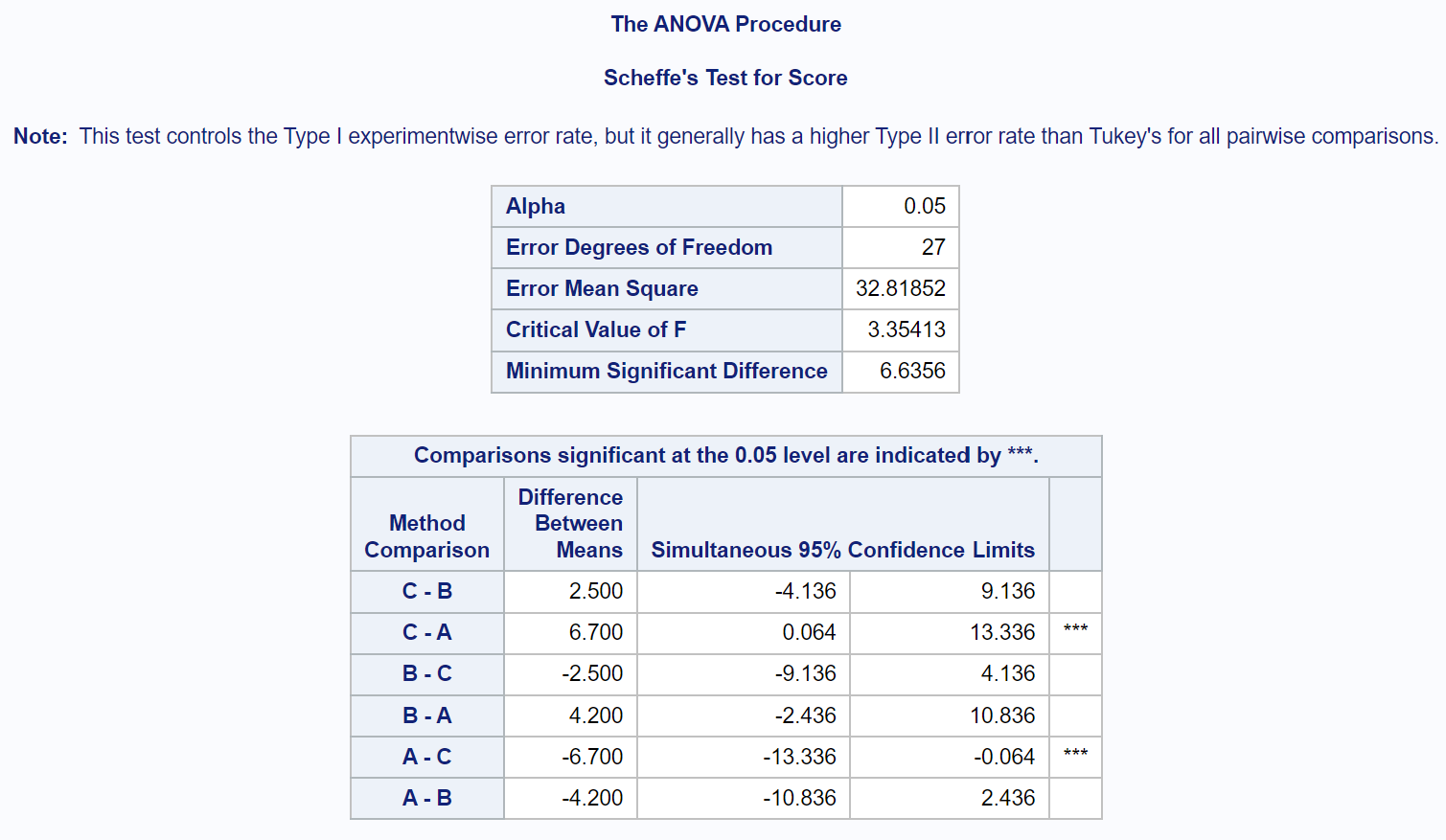
Aby dowiedzieć się, które średnie grupowe są różne, musimy sprawdzić, które porównania parami mają obok siebie gwiazdki ( *** ).

Z tabeli wynika, że istnieje statystycznie istotna różnica w średnich wynikach egzaminów pomiędzy grupą A i grupą C.

Nie ma istotnych statystycznie różnic pomiędzy średnimi pozostałych grup.

W szczególności widzimy, że średnia różnica w wynikach egzaminów pomiędzy grupą C i grupą A wynosi 6,7 .

95% przedział ufności dla różnicy średnich między tymi grupami wynosi [0,064; 13,336] .

Dodatkowe zasoby

Poniższe tutoriale dostarczają dodatkowych informacji o modelach ANOVA:

Przewodnik po korzystaniu z testów post-hoc z ANOVA
Jak wykonać jednokierunkową ANOVA w SAS
Jak wykonać dwukierunkową ANOVA w SAS